2015-05-30
445
Общее уравнение плоскости.
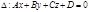
Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)
Если С=0 то вектор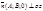 
. Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.
Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0.
Если А=В=0 то уравнение примет вид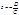 
плоскость параллельна плоскости Oxy.
Если A=B=D=0, то уравнение имеет вид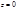 
. Это уравнение плоскости Oxy.
Уравнение плоскости, проходящей через три точки
К (х1;у1) М (х2;у2) N (x3;y3)
Возьмем на плоскости точку P (x;y;z).
Составим векторы:
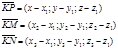
Эти векторы лежат в одной плоскости, следовательно они компланарны:
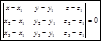
Конические поверхности.
Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р) называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей.
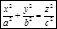- уравнение конуса
3 БИЛЕТ:
Нормальное уравнение плоскости. Уравнение плоскости в отрезках
|
|
|
Уравнение плоскости в отрезках.
Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:
; 
; 
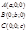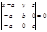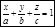
Нормальное уравнение плоскости.
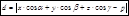
Эллипсоиды.
Рассмотрим сечение поверхности с плоскостями, параллельными xOy. Уравнения таких плоскостей z=h, где h – любое число. Линия, получаемая в сечении, определяется двумя уравнениями:
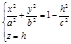
Если |h|>c, c>0, то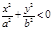 
точек пересечения поверхности с плоскостями z=h нет.
Если |h|=c, т.е. h=±c, то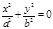 
. Линия пересечения вырождается в две точки (0;0;с) и (0;0;-с). Плоскости z=c и z=–c касаются поверхности.
Если |h|<c, то уравнения можно переписать в виде: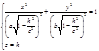 
Линия пересечения есть эллипс с полуосями.
Эллипсоид – замкнутая овальная поверхность, где a,b,с – полуоси. Если все они различны, то эллипсоид называется трехосным. Если какие-либо две полуоси равны, то тело называется эллипсоид вращения, если a=b=c, то тело называется сферой x2+y2+z2=R2
4 БИЛЕТ:
Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей. Расстояние от точки до плоско 
сти.
