Вопрос.
Множество – любая совокупность объектов произвольной среды, каждый из которых называется, элементом
Подмножество – множество, которое является элементом другого множества
Пересечение множеств – множество, состоящее из элементов, которые принадлежат обоим множествам.
Свойства:
1) 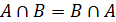
2) 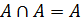
3) 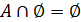
4) 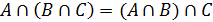
Объединение – множество, состоящее из элементов, принадлежащих хотя бы одному из всех рассматриваемых множеств.
Свойства:
1) 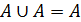
2) 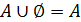
3) 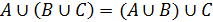
4) 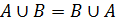
Разность множеств – множество, состоящее только элементов множества А, которые не принадлежат множеству В.
Свойства:
1) 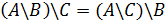
2) 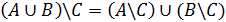
3) 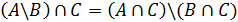
4) 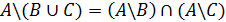
5) 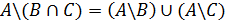
Дополнение – множество, состоящее из разности универсального множества и рассматриваемого.
Свойства:
1) 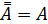
2) 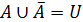
3) 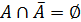
Свойства математических операций:
1) 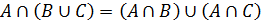
2) 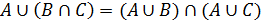
3) 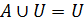
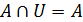
4) 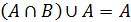
5) 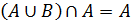
6) 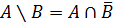
Мощность множества – количество элементов множества
Вопрос.
Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из общей совокупности в n элементов
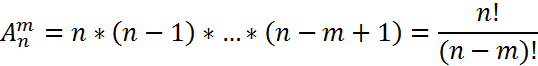
Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из общей совокупности в n элементов
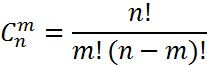
Перестановкой из n элементов называется любой упорядоченный набор из этих элементов
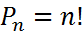
Основная теорема комбинаторики:
Пусть имеется k групп, причем в i-ой группе ni элементов
Выбираем по одному элементу из каждой группы, тогда число способов, которыми это можно сделать вычисляется по формуле:
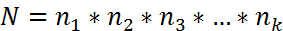
Вопрос.
Элементарный исход – каждый из возможных результатов испытания
Достоверное событие – событие, происходящее при любом исходе
Невозможное событие – событие, которое никогда не произойдет
События A и B называются несовместными, если они не могут произойти в одном и том же испытании
События A и B называются совместными, если они могут произойти в одном и том же испытании
Суммой событий A и B называется событие C, состоящее из тех исходов, которые принадлежат хотя бы одному из множеств.
Произведение событий A и B – событие состоящие из событий A и B одновременно.
Дополнением к событию A называется событие (Противоположное данному), которое происходит тогда и только тогда, когда не происходит событие A.
Вероятность события – функция, удовлетворяющая всем аксиомам:
1) Вероятность не отрицательна
2) Вероятность достоверного события равна единице
3) Вероятность суммы двух несовместимых событий равна сумме их вероятностей.
Свойства:
1) 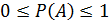
2) 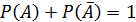
3) 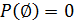
4) 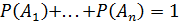
Вопрос.
Формула классической вероятности:
Пусть пространство элементарных исходов конечно и все исходы равновозможны
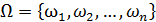
Так как это полная группа несовместных событий, то
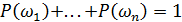
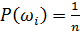
Тогда:
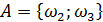
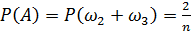
Таким образом, вероятность А:
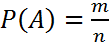
n – общее число исходов
m – число благоприятных исходов
Ω - некоторая область, имеющую меру:
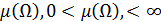
А – некоторая подобласть Ω
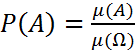
Метод Монте-Карло:
Пусть требуется вычислить
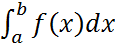 ,
,
(a; b) – границы интегрирования
с – максимальное значение функции,
Тогда:
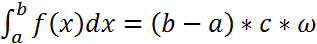 , где w – вероятность попадания некоторой точки (x; y) в прямоугольник площадью [a; b] x [0; c]
, где w – вероятность попадания некоторой точки (x; y) в прямоугольник площадью [a; b] x [0; c]
При проведении опыта с бросанием множества точек (при больших значениях n), получаем
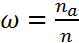
Где na – количество попаданий в область А
Вывод формулы Симпсона:
1) 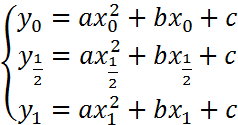
Рассмотрим для одного интервала,
2) n=1, 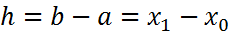
Середина интервала:
3) 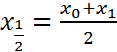
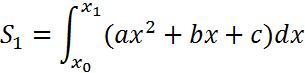
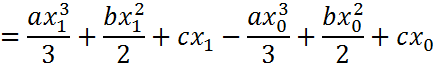
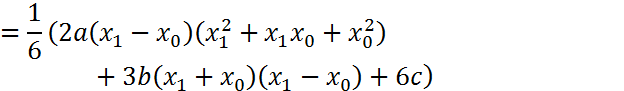
Вынесем h (по формуле 2):
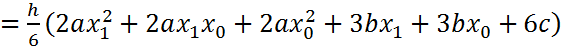
Подставим y0 и y1 (формула 1):
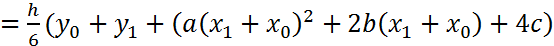
Преобразуем остаток при помощи формулы 3):
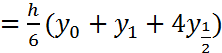
5 Вопрос:
Условной вероятностью события B при условии, что событие A произошло называется отношение вероятности произведения событий A и B к вероятности события А.
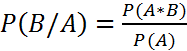
Два события независимы, если вероятность появления события A не меняет вероятности события В.
События A1, A2, An называются независимыми в совокупности, если они независимы попарно, по трое и т.д.
Формулы произведения вероятностей:
1) 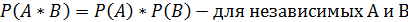
2) 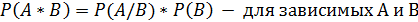
3) 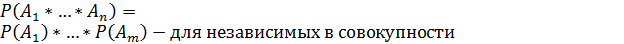
4) Для обратного случая:
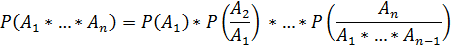
Формулы суммы вероятностей:
1) 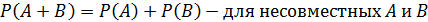
2) 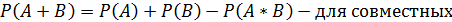
3) 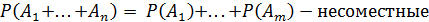
4) 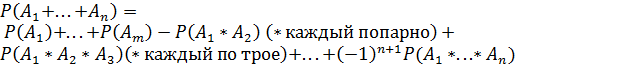
Вопрос.
Схема Бернулли:
Проводим опыт, в котором вероятность наступления события A равна p=P(A)
Определить вероятность того, что событие А появится m раз при повторении однотипного независимого опыта n раз.
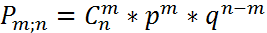
Число m0 называется наивероятнейшим числом наступления А в n испытаниях, если
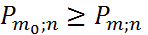 для любого m
для любого m
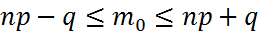
Формула Пуассона используется, когда n – велико, а вероятность события стремится к нулю.
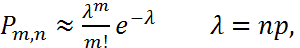
справедливо и при 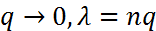
Некоторые рекомендации по применению формулы:
1) При n=10 и 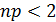
2) При n=100 и 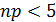
3) При n=1000 и 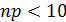
Формулы Муавра-Лапласа используются, если n – велико, а p и q не близки к нулю.
Некоторые рекомендации по применению формулы:
1) При n=10 и 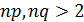
2) При n=100 и 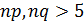
3) При n=1000 и 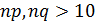
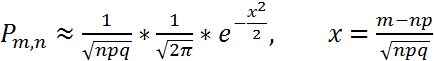
Если выполняется условие применения формулы Муавра-Лапласа, то вероятность появления события A в n испытаниях от m1 до m2
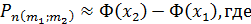
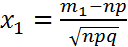
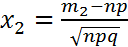
Ф – интеграл Лапласа:
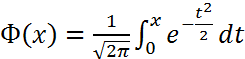
Причем:
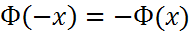
Одним из следствий совместного применения формул сложения и умножения вероятности – формула полной вероятности.
Пусть событие А может наступить при условии наступления одного из событий 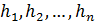 , образующих полную группу несовместных событий
, образующих полную группу несовместных событий
События попарно несовместны и в результате опыта происходит одно из них.
События 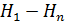 – будут гипотезами, и так как это полная группа, то
– будут гипотезами, и так как это полная группа, то
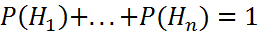
Тогда вероятность события А вычисляется по формуле:
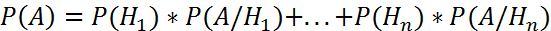
Формула Байеса
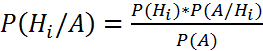
Вопрос.
Пусть производится n независимых испытаний (независимых) в которых событие A появилось m раз, причем вероятность появления события A в каждом испытании одинаково.
Обозначим:
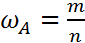 – относительная частота события A
– относительная частота события A
Слабый закон больших чисел.
Относительная частота неограниченно приближается к вероятности события:
Для любого 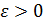 выполняется:
выполняется:
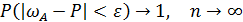
Вопрос.
Случайная величина – функция, ставящая в соответствие число X=X(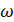 )
)
Дискретная случайная величина – счетная или конечная
Непрерывная случайная величина – величина, принимающая значение из некоторого интервала.
Законом распределения непрерывной случайной величины называется таблица, состоящая из двух строк, в первой строке перечисляются всевозможные значения x, а во второй вероятности, с которыми она их принимает.
Математическое ожидание – сумма произведений ее значений на соответствующие вероятности:
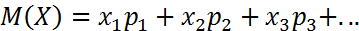
Замечание: Пусть случайная величина приняла значение Хk nk раз в n испытаниях
Из законы больших чисел:
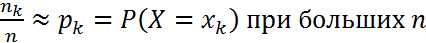
Тогда математическое ожидание равно среднему арифметическому наблюдаемых значений Х при больших n
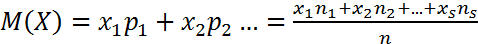
Свойства:
1) 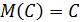
2) 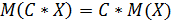
3) 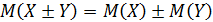
4) 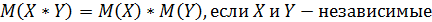
Дисперсия – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
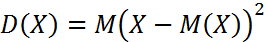 , или же:
, или же:
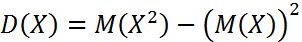
Свойства:
1) 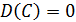
2) 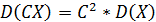
3) 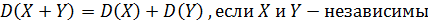
4) 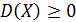
Среднеквадратическое отклонение – квадратный корень из дисперсии
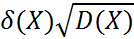
Примечание:
Для схемы Бернулли:
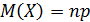
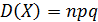
Вопрос.
Функция распределения – вероятность:
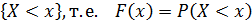
Свойства:
1) 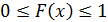
2) 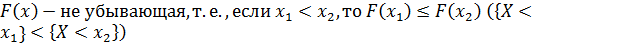
3) 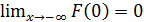
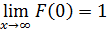
4) 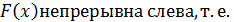
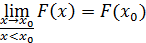
5) 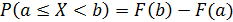
Плотностью распределения называется функция f(x) удовлетворяющая равенству:
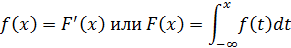
Свойства:
1) 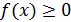
2) 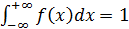
3) 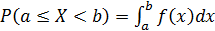
Математическое ожидание – интеграл вида:
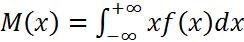
Также это абсцисса центра тяжести криволинейной трапеции постоянной плотности ограниченной функции f(x)
Дисперсия – математическое ожидание квадрата отклонения величины Х от математического ожидания самой величины.
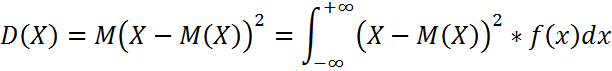
Замечание:
Свойства дисперсии сохраняются:
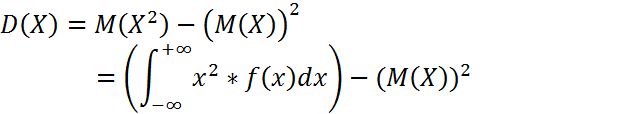
Среднеквадратическое отклонение – квадратный корень из дисперсии
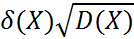
Вопрос.
Геометрическое распределение, математическое ожидание:
При геометрическом распределении, мы рассматриваем появление события A в серии испытании. Поэтому закон распределения будет иметь вид:
| X | 1 | 2 | 3 | 4 | 5 | n |
| P | p | qp | q2p | q3p | q4p | qn-1p |
В связи с этим математическое ожидание:
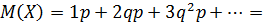
Разложим числовые коэффициенты на подобные члены:
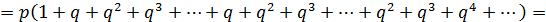
Получаем бесконечное число геометрических прогрессий
(А так как сумма прогрессии равна: 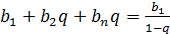 )
)
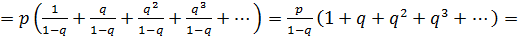
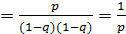
Функция надежности:
Пусть некоторое устройство начинает работать в момент времени t0 = 0, а по истечении времени длительностью t происходит отказ. Обозначим через Т НСВ - длительность времени безотказной работы устройства. Если устройство проработало безотказно время меньшее t, то, следовательно, за время длительностью t наступит отказ. Тогда функция распределения:
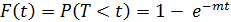
Обратная ей функция – функция надежности:
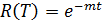
Вопрос.
Дискретная двумерная случайная величина – случайная величина возможные значения которой есть пары чисел (x; y), которые являются дискретными величинами.
Законом распределения дискретной двумерной случайной величины называется перечень возможных ее значений и вероятностей, с которыми она их принимает.
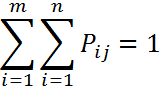
Зная закон распределения двумерной случайной величины, можно найти законы распределения ее составляющих:
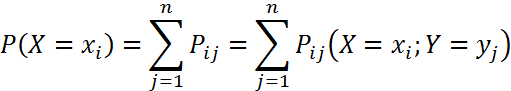
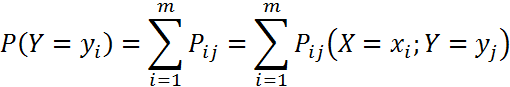
 2018-02-13
2018-02-13 877
877







