Математическое ожидание

        

 

Коэффициент корреляции – выражение вида:

Свойства:

1)  , если величины X и Y – независимы

2)

3)

 

Вопрос.

Генеральная совокупность – совокупность всех значений, полученных в результате опыта.

 

Выборочная совокупность – часть генеральной совокупности, охватываемая данным экспериментом.

 

Имеем выборочную совокупность

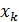Пусть значение наблюдалось раз,  - раз,  -  раз

 

Варианта – наблюдаемые значения  выборочной совокупности

 

Вариационный ряд – варианты, расположенные в возрастающем порядке

 

Числа наблюдений  – называются частотами

 – относительная частота

Статистическое распределение выборки – перечень вариант и соответствующих частот (или относительных частот)

 

Полигон частот – ломаная линия, соединяющая точки  (или относительные частоты )

 

Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы заданной длины а высоты равны соотношению:  (или )

 

Вопрос.

Эмпирическая функция распределения F*(x) называется относительная частота события: X <x, то есть:

Свойства:

1)

2)

3)

Выборочное среднее – среднее арифметическое в значении признака X, т.е.:

 

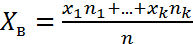
Характеризует математическое ожидание функции

 

Выборочная дисперсия – среднее арифметическое квадратов отклонений значений признака X от

   

Или

   

Характеризует рассеивание значений количественного признака х вокруг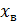

 

Выборочным среднеквадратическим отклонением называется квадратный корень из выборочной дисперсии

Характеризует рассеивание значений случайной величины относительно ее математического ожидания

 

 

 

Вопрос

Статистическая гипотеза – любое предположение о виде теоретической функции распределения F(x), обозначается

 

Статистический критерий – правило, позволяющее по выборке принять гипотезу или опровергнуть

 

Уровень значимости - допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки.

 

Теоретические частоты:

 

 

 

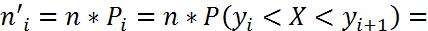
Критерий Пирсона строится на основе специально подобранной случайной величины

 

m – число интервалов

 – эмпирические частоты

 – теоретические частоты

 

Случайная величина  может принимать различные значения:

1)

2)

 – критическое значение критерия, которое затабулировано по заданному уровню значимости альфа и по числу степеней свободы:

 

 

Точечная оценка неизвестного параметра  построенной по выборке  называется функция, зависящая от :

 

Свойства:

1) Оценка  - параметра  называется несмещенной, если выполняется это равенство: