3. Үшбұрыштың ауданын есептеу. Бір түзуде жатпайтын үш 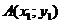
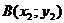
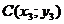 нүктелері берілсін. АВС үшбұрыштың ауданын анықтайтын формуланы шығарайық. АВ және АС кесінділері арасындағы бұрышты
нүктелері берілсін. АВС үшбұрыштың ауданын анықтайтын формуланы шығарайық. АВ және АС кесінділері арасындағы бұрышты 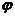 және олардын ұзындықтарын сәйкес d және d1 арқылы белгілейміз. Онда АВС үшбұрыштын ауданы
және олардын ұзындықтарын сәйкес d және d1 арқылы белгілейміз. Онда АВС үшбұрыштын ауданы 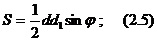 формуласымен анықталады.
формуласымен анықталады.
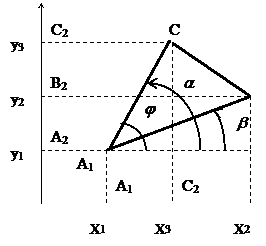
Осы формулада 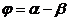 (3-сурет)
(3-сурет)
Олай болса 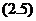 формуласынан табамыз
формуласынан табамыз
|
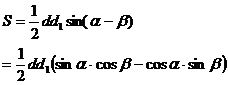
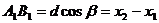
|
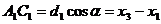

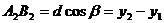
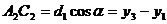
Онда 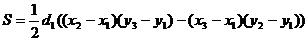 немесе
немесе 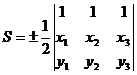 (2.6)
(2.6)
Төбелерінің координаталары берілген үшбұрыштын ауданы (2.6) формуласы бойынша анықталады.
Мысал: Үшбұрыштың төбелері берілсін 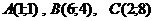 . АВС үшбұрышының ауданын табу керек.
. АВС үшбұрышының ауданын табу керек.
Шешімі: Мұнда  . (2.6) формуласын қолданып табамыз:
. (2.6) формуласын қолданып табамыз: 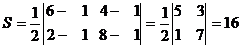
Мысалы-3: 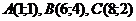 нүктелері берілген. АВС үшбұрышының ауданын тап.
нүктелері берілген. АВС үшбұрышының ауданын тап.
Шешуі: Формула бойынша:
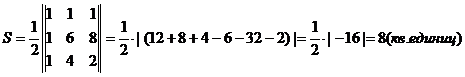 .
.
Анықтама: Түзу – х, у айнымалыларына байланысты координаталары бірінші дәрежелі теңдеуді қанағаттандыратын, жазықтықтағы нүктелердің геометриялық орны болып табылады.
Берілген сызықтың кез келген нүктесінің координаттары х пен у қанағаттандыратын, ал сызықтың бойында жатпайтын кез келген нүктенің координаттары қанағаттандырмайтындай теңдеуді осы сызықтың теңдеуі деп аталады.
Жалпы сызықтың теңдеуі: F(х,у) = 0 немесе у = f(х) түрінде жазылады
1. Бұрыштық коэффициенті бар түзу теңдеуі.
Түзу сызықтың теңдеуін құру үшін ол сызықтың координат жүйесінде қалай орналасқан туралы белгілі бір шарттары болуы керек. Айталық ОХ осіне түзу сызық 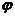 бұрышын құрсын және ол ОУ осінде А(о,в) нүктесінде қиылысады.
бұрышын құрсын және ол ОУ осінде А(о,в) нүктесінде қиылысады.
k=tg 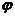 осы түзудің бұрыштық
осы түзудің бұрыштық
коэффициенті. Түзу сызық В және М
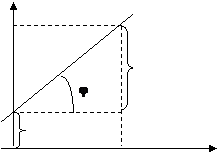 y С(х,у) нүктелерінен өтеді.
y С(х,у) нүктелерінен өтеді.
у АВС ұшбұрыштан (8 – сурет)
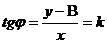 осы өрнектен шығады
осы өрнектен шығады
у-в
А в В
0 х X
Шығарылған (2.17) теңдеуді бұрыштық коэфициенті бар түзу сызықтың теңдеуі деп атайды. Егер в=0 болса, түзу координат басы арқылы өтеді.
2. Бір нүкте арқылы берілген бағытта өтетін түзудің теңдеуі.
Айталық, түзу сызықта жататын 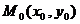
 нүкте берілсін және түзу сызықтың ОХ осіне көлбеу бұрышы
нүкте берілсін және түзу сызықтың ОХ осіне көлбеу бұрышы 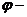 ға тең. Түзу сызықта бір айнымалы координаталары бар М(х,у) нүктесін алайық, түзу сызық
ға тең. Түзу сызықта бір айнымалы координаталары бар М(х,у) нүктесін алайық, түзу сызық 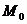 нүктеден өтетін болғандықтан, оның координаталары (2.17) теңдеуді қанағаттандырады
нүктеден өтетін болғандықтан, оның координаталары (2.17) теңдеуді қанағаттандырады 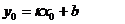 осыдан
осыдан 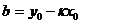
Табылған b – мәнін (2.17) теңдеуге қоямыз, сонда 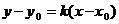 (2.18) теңдеуі шығады. (2.18) теңдеуді бір нүкте арқылы берілген бағытта өтетін теңдеу деп атайды.
(2.18) теңдеуі шығады. (2.18) теңдеуді бір нүкте арқылы берілген бағытта өтетін теңдеу деп атайды.
Мысал: ОХ осіне көлбеу бұрышы 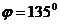 және
және 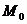 (-5;6) нүктесі арқылы өтетін түзудің теңдеуін жазайық
(-5;6) нүктесі арқылы өтетін түзудің теңдеуін жазайық
Шешімі. Мұнда 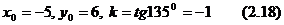 теңдеуін қолданып
теңдеуін қолданып 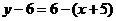 не болмаса
не болмаса 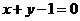 теңдеуі шығады.
теңдеуі шығады.
3. Екі нүкте арқылы өтетін түзудің теңдеуі.
Айталық жазықтықта екі 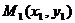 және
және 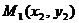 нүктелері берілсін. Осы екі нүкте арқылы өтетін түзудің теңдеуін құрайық. Ол үшін (2.18) теңдеуін қолданайық, сонда
нүктелері берілсін. Осы екі нүкте арқылы өтетін түзудің теңдеуін құрайық. Ол үшін (2.18) теңдеуін қолданайық, сонда 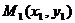 нүкте арқылы өтетін түзулер шоғының теңдеуін аламыз
нүкте арқылы өтетін түзулер шоғының теңдеуін аламыз 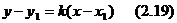
Түзу 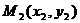 нүкте арқылы өтетін болғандықтан, осы нүктенің координаталары жоғарыдағы теңдеуді қанағатандырады. Сондықтан
нүкте арқылы өтетін болғандықтан, осы нүктенің координаталары жоғарыдағы теңдеуді қанағатандырады. Сондықтан 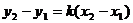 осыдан
осыдан 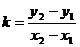
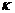 -мәнін
-мәнін 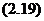 теңдеуге қойғанда
теңдеуге қойғанда 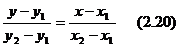 теңдеуді анықтаймыз.
теңдеуді анықтаймыз.
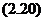 формуласын екі нүкте арқылы өтетін түзудің теңдеуі деп айтады.
формуласын екі нүкте арқылы өтетін түзудің теңдеуі деп айтады.
Мысал. 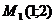 және
және 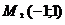 нүктелерден өтетін түзу сызықтың теңдеуін жазыңыз.
нүктелерден өтетін түзу сызықтың теңдеуін жазыңыз.
Шешімі. Мұндағы 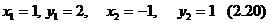 теңдеуге қалып
теңдеуге қалып 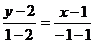 не болмаса
не болмаса 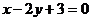
Кесінді арқылы берілген түзудің теңдеуі. Түзудің Ах+Ву+С=0 жалпы теңдеуі берілсін, мұнда А≠0, В≠0, С≠ 0. Осы теңдеуден Ах+Ву=-С немесе 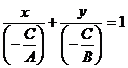 немесе
немесе 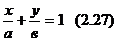
(2.27) кесінді арқылы берілген теңдеу деп аталады. Мұндағы а= 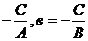 сандары түзудің сәйкес ОХ және ОУ координаталар осьтерін қиятын кесінділер шамалары.
сандары түзудің сәйкес ОХ және ОУ координаталар осьтерін қиятын кесінділер шамалары.
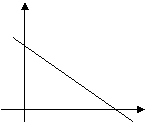
Мысал. Айталық 3х+5у-15=0 түзудің теңдеуі берілсін. Кесінді арқылы берілген теңдеудің түріне келтіру керек және оның графигін салыңыз Шешімі: Берілген теңдеуден табамыз 3х+5у=15.
 у Осы теңдеудің екі жағында 15 бөлеміз.
у Осы теңдеудің екі жағында 15 бөлеміз.
 3 онда
3 онда 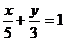
5
х
10 -шы сурет
Мұндағы а=5 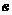 =3 сәйкес ОХ және ОУ остеріндегі берілген түзудің қиған кесінділерінің (10-сурет) шамалары.
=3 сәйкес ОХ және ОУ остеріндегі берілген түзудің қиған кесінділерінің (10-сурет) шамалары.
Жазықтықтағы екі түзудін арасындағы бұрыш. Параллельдік және перпендикулярлық шарттары.
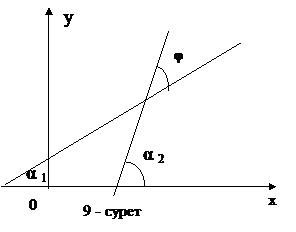 Жазықтықтағы жатқан бұрыштық коэфициент арқылы берілген түзулерді
Жазықтықтағы жатқан бұрыштық коэфициент арқылы берілген түзулерді 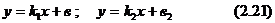 қарастырайық. Олардың арасындағы бұрыш
қарастырайық. Олардың арасындағы бұрыш 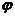 -ға тең,ал әр біреуінің Ох өсінің оң бағытымен жасалатын бұрыштары
-ға тең,ал әр біреуінің Ох өсінің оң бағытымен жасалатын бұрыштары 
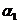 және
және 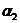 болсын (9-сурет).Онда
болсын (9-сурет).Онда 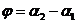 болады.
болады.
Енді осы бұрышқа айырманың
тангенсін пайдаланып,
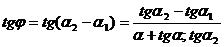
теңдігін аламыз.
Мұнда 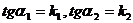
болғандықтан 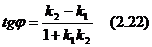

(2.22) формула жазықтықта берілген кез келген екі түзу арасындағы тангенсін анықтайды. Осы теңдеуді шешу 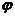 бұрышын табамыз.
бұрышын табамыз.
Енді екі (2.21) түзулер өзара параллель бөлу үшін, олардың арасындағы бұрыш 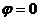 бөлу керек. Ендеше
бөлу керек. Ендеше 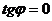 , онда
, онда 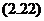 бөлшегінің алымы нөлге тең болуы керек, яғни
бөлшегінің алымы нөлге тең болуы керек, яғни 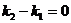 немесе
немесе 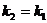 (2.23). Егер екі түзу өзара перпендикуляр болса, яғни
(2.23). Егер екі түзу өзара перпендикуляр болса, яғни 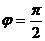 , онда
, онда 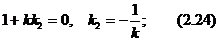
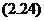 екі түзудің параллельдік және перпендикулярлық шарты деп аталады.
екі түзудің параллельдік және перпендикулярлық шарты деп аталады.
Мысал: 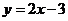 және
және 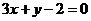 түзулерінің арасындағы бұрышты табыңдар.
түзулерінің арасындағы бұрышты табыңдар.
Шешімі: 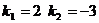 онда
онда 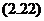 формуланы қолданып
формуланы қолданып 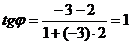 осыдан
осыдан 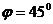 болады.
болады.
Мысал: 2х-3у+1=0 түзуге параллель және М(1:2) нүктеден өтетін түзу сызықтың теңдеуін құрыңыз.
Шешімі: Ізделінген теңдеуді (2.18) теңдеу түрінде жазамыз
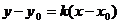
Берілген теңдеуден параллельдік шарт арқылы бұрыштық коэфициентті табамыз 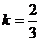 және мұнда
және мұнда 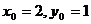 . Осыдан
. Осыдан 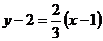 не болмаса 2х-3у+4=0.
не болмаса 2х-3у+4=0.
Мысал: М(- 1:1) нүктеден өтетін және 3х-у+2=0 түзуге перпендикуляр болатын түзу сызықтың теңдеуін жазыңыз.
Шешімі: Берілген түзудің бұрыштық коэфициентті 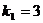 Перпендикулярдық шарт (2.24) арқылы
Перпендикулярдық шарт (2.24) арқылы 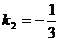 екенін табамыз. Және мұнда
екенін табамыз. Және мұнда 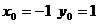 , онда ізделген теңдеу
, онда ізделген теңдеу 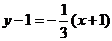 немесе
немесе 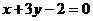 болады.
болады.
Түзудің қалыпты (нормальдық) теңдеуі. Нүкте мен түзудің ара қашықтықтығы.
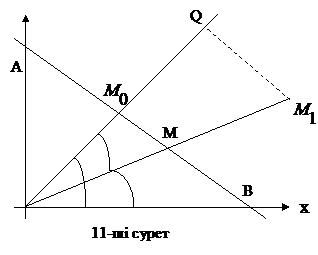 Айталық АВ түзу сызығы берілсін, Бас нүкте арқылы, АВ-ға перпендикуляр N түзуін өткізейік..АВ мен N қилысу нүктесін
Айталық АВ түзу сызығы берілсін, Бас нүкте арқылы, АВ-ға перпендикуляр N түзуін өткізейік..АВ мен N қилысу нүктесін 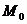 - белгілейміз (11-сурет)
- белгілейміз (11-сурет)
Y
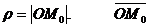 векторымен
векторымен
ОХ арасындағы бұрыш 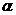 - тең
- тең
болсын. 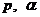 белгілі деп,
белгілі деп,
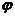 АВ түзуінің теңдеуін құру
АВ түзуінің теңдеуін құру
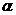
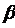 керек. Осы түзуде кез келген М(х;у)
керек. Осы түзуде кез келген М(х;у)
нүктесін алайық
.
Мұнда 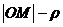 деп белгілеп
деп белгілеп 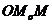 ұшбұрышынан табамыз
ұшбұрышынан табамыз 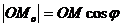 , немесе
, немесе 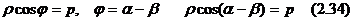 .
.
(2.34) формуласын жіктеп 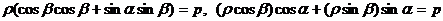 және
және  екенін ескере отырып шығарамыз:
екенін ескере отырып шығарамыз: 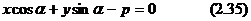
Осы (2.35) анықталған АВ түзудің теңдеуін қалыпты (нормальдық) теңдеу дейді.
Нүктеден түзуге дейінгі қашықтық.
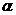 - нормальдің полярлық бұрышы,
- нормальдің полярлық бұрышы, 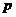 - бас нүктеден АВ түзуіне дейінгі қашықтығы. АВ түзуінен тыс жатқан
- бас нүктеден АВ түзуіне дейінгі қашықтығы. АВ түзуінен тыс жатқан 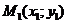 нүкте болсын. АВ түзуінен
нүкте болсын. АВ түзуінен 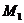 нүктесіне дейінгі қашықтығын
нүктесіне дейінгі қашықтығын  d деп белгілейік (11 сурет)
d деп белгілейік (11 сурет)
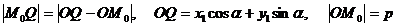 сондықтан
сондықтан
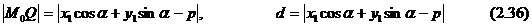
(2.36) формуласы 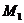 нүктесі мен АВ түзуінің ара қашықтығын анықтайтын формула. Сондықтан кез келген
нүктесі мен АВ түзуінің ара қашықтығын анықтайтын формула. Сондықтан кез келген 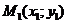 нүктеден АВ түзуіне дейін қашықтықты табу үшін
нүктеден АВ түзуіне дейін қашықтықты табу үшін 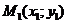 нүктенің координаталарын түзудің қалыпты (2.35) теңдеуіне қойып абсолют шамасын алу керек.
нүктенің координаталарын түзудің қалыпты (2.35) теңдеуіне қойып абсолют шамасын алу керек.
Айталық бір түзу жалпы және қалыпты теңдеулер түрінде берілсін. 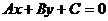 және
және 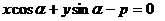 .Осы теңдеулер бір түзуді анықтағандықтан олардың айнымалылары х,у алдында тұрған сәйкес коэффициенттері өз ара пропорционал болуы керек, яғни
.Осы теңдеулер бір түзуді анықтағандықтан олардың айнымалылары х,у алдында тұрған сәйкес коэффициенттері өз ара пропорционал болуы керек, яғни 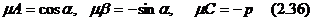 Бұдан
Бұдан 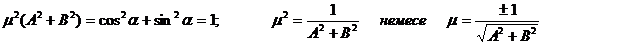
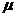 - санын қалыптаушы көбейткіш деп атайды. Қалыптаушы көбейткіш алдындағы таңбаны таңдау үшін (2.36) формулалардың үшінші теңдігін қолданамыз.
- санын қалыптаушы көбейткіш деп атайды. Қалыптаушы көбейткіш алдындағы таңбаны таңдау үшін (2.36) формулалардың үшінші теңдігін қолданамыз. 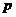 оң сан болғандықтан
оң сан болғандықтан 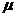 таңбасын жалпы теңдеудің бос мүшесінің таңбасына теріс таңба қылып аламыз. Егер
таңбасын жалпы теңдеудің бос мүшесінің таңбасына теріс таңба қылып аламыз. Егер 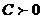 , онда
, онда 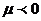 , ал
, ал 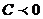 болса, онда
болса, онда 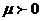 болады. Қортып айтқанда жалпы теңдеуді қалыпты теңдеуге айналдыру үшін оны қалыптауыш көбейткішке көбейту керек, яғни
болады. Қортып айтқанда жалпы теңдеуді қалыпты теңдеуге айналдыру үшін оны қалыптауыш көбейткішке көбейту керек, яғни 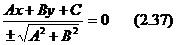 .
.
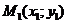 нүктесінен
нүктесінен 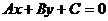 түзуіне дейінгі қашықтық
түзуіне дейінгі қашықтық 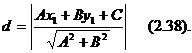 формуласымен анықталады.
формуласымен анықталады.
Мысал. 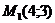 нүктесінен
нүктесінен 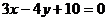 түзуіне дейінгі ара қашықтықты анықтаңыз.
түзуіне дейінгі ара қашықтықты анықтаңыз.
Шешімі: Мұнда 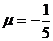 . Берілген теңдеуді қалыпты (2.37) түріне келтіреміз:
. Берілген теңдеуді қалыпты (2.37) түріне келтіреміз: 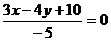 , ал ара қашықтықты анықтау үшін (2.38) формуласын қолданамыз:
, ал ара қашықтықты анықтау үшін (2.38) формуласын қолданамыз:  .
.
Мысал: 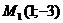 нүктесінен
нүктесінен 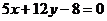 түзуіне дейінгі ара қашықтықты анықтаңыз.
түзуіне дейінгі ара қашықтықты анықтаңыз.
Шешімі: Формула бойынша:
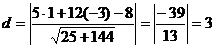 .
.
Түзулер шоғының теңдеуі. Жазықтықта 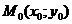 нүктеден өтетін түзу сызықтар жиынтығын түзу сызықтар шоғы деп атайды.
нүктеден өтетін түзу сызықтар жиынтығын түзу сызықтар шоғы деп атайды. 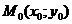 нүктеден өтетін екі түзудің теңдеулері берілсін
нүктеден өтетін екі түзудің теңдеулері берілсін 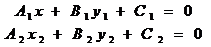 . Осыдан
. Осыдан 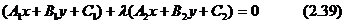 теңдеуін құрамыз. Осы теңдеуді
теңдеуін құрамыз. Осы теңдеуді 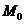 нүктенің координаталары қанағаттандырғандықтан, бұл түзу
нүктенің координаталары қанағаттандырғандықтан, бұл түзу 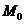 нүктеден өтеді. Сондықтан
нүктеден өтеді. Сондықтан 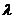 -ға нольге тең емес әр шамаларды берсе, онда (2.39)
-ға нольге тең емес әр шамаларды берсе, онда (2.39) 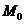 нүктеден өтетін түзулер шоғының теңдеуін анықтайды.
нүктеден өтетін түзулер шоғының теңдеуін анықтайды.
Мысал. Айталық екі түзу берілсін 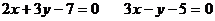 . Осы екі түзудің қиылысу нүктесінен және
. Осы екі түзудің қиылысу нүктесінен және 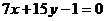 түзуіне перпендикуляр болатын түзудің теңдеуін құру керек.
түзуіне перпендикуляр болатын түзудің теңдеуін құру керек.
Шешімі: (2.39) теңдеуді пайдаланып 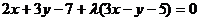 қиылысу нүктесінен өтетін түзулер шоғының теңдеуін жазамыз. Осыдан
қиылысу нүктесінен өтетін түзулер шоғының теңдеуін жазамыз. Осыдан 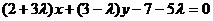 . Екі түзудің перпендикулярлық (2.33) шартын қолданып
. Екі түзудің перпендикулярлық (2.33) шартын қолданып 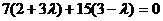 .
. 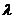 -ны табамыз, яғни
-ны табамыз, яғни 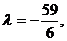
онда ізделінген теңдеу 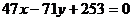 болады .[
болады .[
 2018-02-20
2018-02-20 946
946








