2018-02-20
760
болатын нүктелер бұрыштық деп аталады.
Туындының экономикалық мағынасы
Өндірілген өнім мөлшерінен уақыт бойынша туындының еңбек өнімділігін беретінін көрдік. Енді туындының экономикалық мағынасын көрсететін тағы бір ұғымды береміз.
Өндіріс шығындарын өндірілетін өнімнің мөлшері х-ке тәуелі функция ретінде карастырамыз. Өнімнің өсімі ∆х болса, оңі өндіріс шығынының өсімшесі ∆у, ал өнім бірлігіне жұмсалатын өндіріс шығынының орта өсімшесі ∆у /∆х болады. Сонда туынды у'= lim∆х →0∆у/∆х
өндірстің шекті шығынын береді және косымша өнімнің бірлігіне жұмсалатын қосымша шығынды жуықтап сипаттайды. Шекті шғындар өндіріс күші (шығарылатын өнім көлемі) х -ке тәуелді және тұрақты емес тек айнымалы өндіріс шығындарымен (шикізат, жанармай және т.б.) анықталады. Осы сияқты шекті табыс, шекті өнім, шекті пайдалылық, шекті өнімділік және баска шекті шамаларды қарастыруға болады.
|
|
|
Шекті шамалар экономикалық ұгымдардың өзгеру барысын сипаттайды. Туынды кайсыбір экономикалық объектінің басқа бір объектіге карағанда өзгеру жылдамдығын анықтайды. Кейбір жағдайларда экономикалық көрсеткіштердің үзіліссіз еместігіне қарамастан шекті шамаларды ұтымды пайдалануға болады. Мысал ретінде монополистік және бәсекелік рынок жағдайындағы орта және шекті табыстардың байланысын қараймыз. Өнімді сатқаннан шыққан жиынтық табысты өнім бірлігінің бағасымен өнім санының көбейтіндісі ретінде анықтауға болады:
Монополистік нарық Еркін бәсекелік нарық
r = pq, r — жиынтық табыс, р -өнім бірлігінің бағасы, q —өнім саны. Монополия жағдайында бір немесе бірнеше фирма белгілі саладағы өнім ұсынысын, демек өнім бағасын толығымен қадағалайды. Әрине, бағаның өсуіне байланысты өнімге деген сұраныс азайады. Сұраныстың азаюы р = аq + в, (а < 0, в > 0) кемімелі функциясы арқылы берілсін делік. Мұндағы р = р(q)~ өнім саны q -ға тәуелді сұраныс мөлшері. Соңда сатылған өнімнен түсетін жиынтық табыс r = (аq + в)q=аq2 + вq, өнім бірлігінен түсетін орта табыс rор = r/q = аq+ в, ал шекті табыс, яғни қосымша өнім бірлігінен түсетін қосымша табыс r,q = 2аq+ в болады.
|
|
|
Сонымен монополистік нарық жағдайында сатылған өнім саны өскен сайын шекті табыс кемиді. Ол орта табыстың аз жылдамдықпен азаюуына соқгырады.
Нарыққа өнім шығаратындар өте көп және жеке фирма бағаның деңгейін қадағалай алмайтын бәсекелік жағдайында сатылатын өнім саны тұрақты, мысалы, р = в болады.Сонда жиынтық табыс r = вq, орта табыс rор = r/q = в, ал шекті табыс r,q = в болады.
Сонымен еркін бәсекелестік нарық жағдайында орта және шекті табыстар өзара тең болады.
Экономикалық процесстерді зерттеу үшін көбінесе функцияның икемділік ұғымы қолданылады.
ТУЫНДЫНЫ ТАБУ ЕРЕЖЕЛЕРІ.
және 
табылсын, ал 
- const. Онда
1. 
, шынында да, 
.
2. (C*u) /`=C*u /`
3. 
.
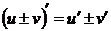4. 
.
5. 
. 
Кері функцияның туындысы.
Егер 
функциясы үшін 
нүктесінде туындысы бар және ол нөлден өзгеше болатындай 
кері функциясы табылса, онда
.
айқын емес функциясының туындысы бар.
Берілген функцияның туындысын табу үшін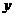 
-тің 
айнымалысына тәуелді функция екенін ескере отырып, теңдіктің екі жағын да дифференциалдаймыз.
ТУЫНДЫНЫҢ КЕСТЕСІ
1.(C) /=0, C=const.. 2. (C * u) /=C * u/. 3. (u + v) /= u /+ v /.
4. (u+v) /=u /* v+u* v /. 5.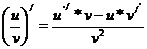 
.
12. 
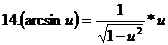
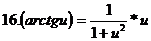
Лекция 10. Дифференциал функциясы. Туындымен байланыс. Функция дифференциалының үздіксіздігі. Дифференциалдау ережесі. Функция дифференциалының қасиеттері.
Жоғары ретті туынды және дифференциалы.
Анықтама 4. 
-ке қатысты сызықтық болатын 
функциясының өсімшесінің негізгі бөлігі функцияның дифференциалы деп аталады және былай белгіленеді: 
.
болсын. Онда 
. Функцияның дифференциалының мынадай қасиеттері бар:
1. 
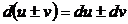
2. 
3. 
4. 
немесе 
болсын. Онда
- бірінші дифференциалдың формасының инварианттылық қасиеті.
5. 
болса, 
теңдігі орынды болғандықтан, жуықтап есептеуде 
деп алуға болады, немесе
(5)
ГЕОМЕТРИЧЕСКИ СМЫСЛ ДИФФЕРИНЦИАЛА: дифференциал функции f(x), соответствующей данным значениям x и dx, равен приращению ординаты касательной к кривой y=f(x) в данной точке x.
Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид dy=f(u)du, кокой он имел бы, если бы промежуточный аргумент u был независимой переменной. Это свойство дифференциала называется инвариантностью формы дифференциала.
ЖОҒАРҒЫ РЕТТІ ТУЫНДЫ ЖӘНЕ ДИФФЕРЕНЦИАЛ
Жоғары ретті туындылар. 
функцияның 
аралығында туындысы бар болса, онда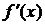 
белгілі функция болады. Өз кезегінде бірінші туындының да 
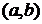аралығында туындысы болуы мүмкін. Бұл жағдайда оны функциясының екінші ретті туындысы дейді және 
немесе 
арқылы белгілейді.
Жалпы - тің 
ретті туындысының туындысы функцияның 
- ші ретті туындысы деп атайды да
немесе 
деп белгілейді. - рет дифференциалданатын 
және 
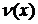функцияларының қосындысы мен көбейтіндісі үшін келесі дифференциалдау ережесі орындалады:
1. 
;
Ферма, Ролля, Лагранж, Коши теоремасы және оның қолданылуы. Лопиталь ережесі және Тейлор формуласы.
Теорема 2. (Ролль). Егер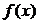 
функциясы 
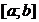сегментінде үзіліссіз және ең
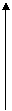олмағанда 
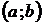интервалында ақырлы
|
|
|
туындылы болып, 
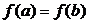теңдігі
у = f(x) орындалса, онда 
орындалатындай 
.
производная f ’(x) обращается в нуль,
Дәлелдеуі. 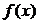функциясы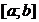
а c b x сегментінде үзіліссіз болғандықтан,
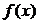функциясы осы аралықта өзінің ең кіші мәні m мен ең үлкен мәні М –ді қабылдайды. Онда, егер m=M 
, 
аралығында 
. 
болсын және 
. Онда х1 және х2 нүктелерінің біреуі интервалының шеткі нүктелеріне тең емес. Ол нүкте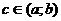 
нүктесі болсын. Ендеше, c нүктесі экстремум нүктесі болғандықтан, 
(сурет15).
Теорема Коши. Егер аралығында 
және 
болса, онда 
Келесі теорема 3 теореманың салдары сияқты қарастырылады.
Теорема Лагранжа: Егер 
, онда 
теңдігі орындалатындай
Теорема Ферма: Егер 
болып және 
нүктесінде экстремумы бар болса, онда
(1)
Тейлора формуласы:
(19.11)
Маклерона формуласы:
, (19.12)
мұндағы 
Лагранж формасының қосымша мүшесі..
Лопиталь ережесі:
Салдар 1. Егер 
, [a;b] аралығында.
Салдар 2. Егер 
, [a;b] аралығында, мұндағы С – const.
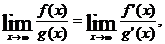
түріндегі анықталмағандарды ашуды, Лопиталь ережесі деп аталады.
Бұл ереже түріндегі дифференциалданатын функцияның шектерін туынды көмегімен есептеуге мүмкіндік береді.
Әдебиеттер тізімі.
Негізгі әдебиеттер:
1. Экономистерге арналған жоғары математика. Н.Ш.Кремер редакциясы, М.,1997ж.
2. Д. Письменный Жоғары математика бойынша лекциялар конспектісі, 1 бөлім, Москва, 2004 ж.
3. Г.Н. Яковлев Математика для техникумов, 2 бөлім, М., 1978ж.
|
|
|
4. А.П. Рябушко Сборник индивидуальных заданий по высшей математике, Минск, 1990 ж.
5. Жоғары математика бойынша бақылау жұмыстары.
Қосымша әдебиеттер:
1. Н.Ш. Крамер Жоғары математика бойынша практикум, М., 2005 ж.
2. Шипачев В.М. Жоғары математика, т.1,2. М.,1985ж.
3. А.Н. Колесников Краткий курс математики для экономистов, 1997 ж.
Лекция 9. Жуықтап есептеуде дифференфиалдың қолданылуы. Дифференециалдық есептеу тәсілімен функцияны зерттеу. Функцияның монотондылық шарттары. Функцияның экстремумы: қажетті және жеткілікті шарты. Дөңес және иілген функция Функцияның асимптотасы және иілу нүктелері. Функция графигін салуда зерттеудің жалпы схемасы.
Жуықтап есептеуде дифференфиалдың қолданылуы.
По определению, ∆y = f(x) - f(x0), то f(x) - f(x0) ≈ f ’(x0) * ∆x, откуда
f(x) ≈ f(x0) + f ’(x0) * ∆x.
Эта формула применяется в приближенных вычислениях.
