Характеристика островершинности

- Эксцесс:

 

. (2.6)

 

, , ,

Получив основные числовые характеристики (положения, рассеяния, асимметрии, островершинности) распределения, можно сделать в первом приближении суждение о нормальности распределения, для которого, как известно, , . Найденные значение коэффициента асимметрии (недостаточно близкое к нулю) указывает, что распределение не симметрично. Эксцесс также отличен от нуля, что говорит о возможном отличии распределения от нормального.

Далее следует более детально проверить гипотезу о нормальности распределения, принятие которой позволяет применять собственно метод анализа вариационных рядов.

Точные параметры гипотетического нормального закона нам неизвестны, поэтому проверим нулевую гипотезу, о нормальности закона распределения концентраций в исследуемых пробах (на примере проб с первого пункта у первого лаборанта). Сформулируем нулевую гипотезу:  F(x) - функция нормального распределения с параметрами  и , и, соответственно, противоположную ей  - не является функцией нормального распределения. В этих гипотезах функция F(x) – это функция распределения концентраций в исследуемых пробах.

Для проверки этой нулевой гипотезы используем найденные выше точечные оценки математического ожидания и среднего квадратического отклонения нормально распределенной случайной величины (концентрации):

 (по формуле 2.1);

 (по формуле 2.3);

При проверке гипотезы о нормальном распределении генеральной совокупности сравниваются эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормальности распределения) частоты. Для этого используются статистика  - Пирсона с  степенями свободы (k - число групп, r - число оцениваемых параметров, в настоящем примере оценивались математическое ожидание и среднее квадратическое отклонение, следовательно, r=2). Если , то нулевая гипотеза отвергается и считается, что предположение о нормальности распределения не согласуется с опытными данными. В противном случае () нулевая гипотеза принимается.

Преобразуем имеющийся ряд измерений (табл. 1) в интервальный вариационный ряд. Для построения такого ряда промежуток изменения концентраций (значений варианта ) разбивается на ряд отдельных интервалов и подсчитывается количество значений величины в каждомиз них.

Будем считать, что отдельные (частичные) интервалы имеют одну и ту же длину. Число интервалов (k) определить по формуле Стерджесса:

 

 (2.7)

 

Соответственно,

Длина частичного интервала определяется по формуле:

 

 (2.8)

 

Вычислим теоретические вероятности р_i попадания СВ  в частичные интервалы [х_i-1; x_i) по формуле:

 

 

Дальнейшие вычисления, необходимые для определения расчетного значения выборочной статистики , сведены в таблицу (табл. 5).

 

Таблица 5

Наблюдаемые значений СВ Х	Частоты, ni	Нормированные интервалы [ui; ui+1]
0,011-0,0128	11	0,12-0,43	0,111	13,32	5,382	0,404
0,0128-0,0136	16	0,43-0,57	0,131	15,72	0,078	0,005
0,0136-0,0145	65	0,57-0,72	0,521	62,52	6,150	0,098
0,0145-0,0154	20	0,72-0,88	0,167	20,04	0,002	0,0001
0,0154-0,018	8	0,88-1,33	0,07	8,4	0,160	0,019
	120		1	120		0,53

Замечание применение критерия , для проверки гипотезы о нормальности распределения предполагает наличие в каждом частичном интервале не менее пяти элементов, в противном случае желательно объединять эти интервалы с соседними. Именно по этому число интервалов сократилось до 5.

В результате вычислений получили . Определим при помощи функции «ХИ2РАСП» (Excel) критическое значение -распределения при заданном уровне значимости  и числе степеней свободы :

Так как , то нет оснований для отклонения нулевой гипотезы H_о, о нормальном законе распределения концентраций в исследуемых пробах с параметрами  и .

Аналогично можно проверить и остальные ряды наблюдений.

Далее проверим статистические гипотезы о наличии загрязняющих веществ в пробах почвы.

Сначала рассмотрим пробы, анализируемые первым лаборантом. Распределения будем считать нормальными.

Выдвинем гипотезу о том что среднее значение концентраций (т.е. математическое ожидание) загрязняющего вещества в выборке 1 у первого лаборанта не превышает 0,015 Иными словами  и противоположную ей - .

Необходимо рассмотреть критерийК=u, где

 

 (2.7)

 

По условию конкурирующая гипотеза имеет вид , поэтому критическая область правосторонняя. Графически эта область изображена на рис 2. Найдем критическую точку из равенства:

 

где Ф - функция Лапласа;

u_кр - квантиль нормального закона распределения, соответствующий уровню, значимости

Согласно приложения 1: , соответственно , поэтому следует принять нулевую гипотезу Н_о, то есть средняя концентрация загрязняющего вещества в выборке 1 у первого лаборанта не превышает ПДК при уровне значимости (т.е нет противоречия гипотезе в 5 случаях из 100).

Выдвинем гипотезу о том что среднее значение концентраций (т.е. математическое ожидание) загрязняющего вещества в выборке 2 у первого лаборанта не превышает ПДК=0,015у.е. Иными словами  и противоположную ей - .

Необходимо рассмотреть критерийК=u, где

 

 

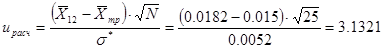
По условию конкурирующая гипотеза имеет вид , поэтому критическая область правосторонняя. Найдем критическую точку из равенства . Согласно приложения 1: , соответственно  поэтому следует отвергнуть нулевую гипотезу Н_о, т.е принять гипотезу . Это означает, что по данным 1 лаборанта в выборке 2 содержится загрязняющее вещество в концентрации выше ПДК.

Далее рассмотрим пробы, анализируемые вторым лаборантом.

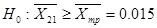Выдвинем гипотезу  о том, что среднее значение концентраций (т.е. математическое ожидание) загрязняющего вещества в выборке 1 у второго лаборанта превышает 0,015. Иными словами  и противоположную ей - .

Необходимо рассмотреть критерийК=u, где

 

 

По условию конкурирующая гипотеза имеет вид , поэтому критическая область левосторонняя. Графически эта область изображена на рис 3. Найдем критическую точку из равенства . Согласно приложения 1: , соответственно , поэтому следует отвергнуть нулевую гипотезу Н_о. Концентрация загрязняющего вещества в выборке 1 у второго лаборанта не превышает 0,015 при уровне значимости (т.е. нет противоречия гипотезе в 5 случаях из 100).

Выдвинем гипотезу о том что среднее значение концентраций (т.е. математическое ожидание) загрязняющего вещества в выборке 2 у второго лаборанта превышает 0,015.  и противоположную ей - .

Необходимо рассмотреть критерийК=u, где

 

 

По условию конкурирующая гипотеза имеет вид , поэтому критическая область левосторонняя. Найдем критическую точку из равенства . Согласно приложения 1: , соответственно , поэтому следует отвергнуть нулевую гипотезу Н_о, т.е. принимается гипотеза . Концентрация загрязняющего вещества в выборке 2 у второго лаборанта не превышает ПДК при уровне значимости (т.е. нет противоречия гипотезе в 5 случаях из 100).

Из результатов видно, что лаборанты имеют различную квалификацию. По результатам анализа 2-ой выборки первым лаборантом, оказалось, что средняя концентрация загрязняющего вещества в исследуемых пробах полигонов выше установленной(0,015), в отличие – у второго лаборанта анализ 2-ой выборки показал обратное.

Проверить значимость этого отличия возможно с помощью критерия t-Стьюдента.

Выдвигаем нулевую гипотезу о том, что результаты, полученные двумя лаборантами не отличаются друг от друга, т. Е.  , при альтернативной гипотезе  - данные существенно различны.

Примем уровень значимости  =0,05, заданный при проведении анализов лаборантами. Так как выборки независимы, то применим критерий t-Стьюдента со степенями свободы .

 

 (2.8)

 

При помощи функции «СТЬЮДРАСП» (EXCEL) определим критическое значение (t-распределения для двусторонней области): t_кр.=t_0,05;43 =2.02, при числе степеней свободы .

Так как , то нулевую гипотезу следует отклонить. Следовательно, различия результатов анализа состава полигона, полученные двумя лаборантами отличаются статистически значимо по величине.

Количество проб веществ, которых будет достаточно для оценки качества полигона можно определить по следующей методике.

Примем ряд допущений:

- Допустим, что проводилась 10%-ная выборка из генеральной совокупности (т.е для проведения анализа в лаборатории было отобрано 10% проб);

- Выборка проводилась случайно и бесповторно;

- Для определения достаточного количества проб вещества зададимся условием уменьшения предельная ошибка выборки в два раза: .

Проведем оценку для данных по обоим пунктам первого лаборанта.

Сначала вычислим предельную ошибку выборки по формуле:

 

 (2.8)

 

где: где t - квантиль нормального закона распределения при 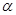=0,05, t=l,96;

N’₁₁- объем генеральной совокупности, т.е. ;

- выборочная оценка дисперсии генеральной совокупности

Имеем

Значит, с доверительной вероятностью  можно утверждать, что средняя концентрация загрязняющих веществ во всей совокупности проб, отобранных на 1 пункте:

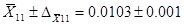
Необходимый объем выборки определяется по формуле:

 

 (2.9)

 

Следовательно,

.

По тому же алгоритму вычислим необходимый объем выборки проб из пункта 2.

Сначала вычислим предельную ошибку выборки по формуле:

 

 (2.10)

 

где: t - квантиль нормального закона распределения при =0,05, t=l,96;

N’₁₂ - объем генеральной совокупности, т.е. ;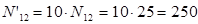

- выборочная оценка дисперсии генеральной совокупности

Имеем .

Значит, с доверительной вероятностью  можно утверждать, что средняя концентрация загрязняющих веществ во всей совокупности проб, отобранных в пункте 2:

.

Чтобы определить необходимый объем выборки, нужно знать какого порядка должна быть необходимая ошибка вычислений. В нашей работе зададимся:

- Предельная ошибка не должна превысить .

Необходимый объем выборки определяется по формуле:

 

 (2.11)

 

Следовательно,

.

Заключение

 

В большинстве случаев загрязнение вод остается невидимым, поскольку загрязнители растворены в воде. Есть несколько природных загрязнителей. Находящийся в земле алюминий попадает в систему пресных водоемов в результате химических реакций. Паводки вымывают из почвы лугов магний, что наносит огромный ущерб рыбным запасам. Однако объем естественных загрязняющих веществ - ничто по сравнению с производимыми человеком.

Основной проблемой, я считаю, являются несанкционированные сбросы сточных вод. Руководители предприятий не заинтересованы в дополнительных затратах связанных с очисткой. Необходимо проводить постоянный контроль за сточными водами, для оценки качества использовать квалифицированных работников. Каждый загрязнитель должен нести ответственность.

В данной курсовой работе был проведён анализ образцов проб сточной воды, поступивших в лабораторию из двух предприятий. Анализ проводился двумя лаборантами, исследовавшими независимо образцы с обоих предприятий. Перед ними была поставлена задача определения наличия концентрации вредного вещества Х.

Была рассмотрена возможность применения одного из методов математической статистики – анализа вариационных рядов для решения поставленной задачи.

В процессе работы выдвигался ряд гипотез о наличии загрязняющего вещества в рассматриваемых пробах, и с помощью методики анализа вариационных рядов выяснялась верность этих гипотез.

По результатам анализа 2-ой выборки (анализ проб со 2 предприятия) первым лаборантом, оказалось, что средняя концентрация загрязняющего вещества в исследуемых пробах выше установленной (0,015), у второго лаборанта анализ 2-ой выборки показал обратное. Был проведён анализ значимости различий полученных лаборантами результатов (с помощью распределения t-Стьюдента), который показал статистическую значимость полученных ими результатов. Учитывая этот факт можно сделать вывод о том, что лаборанты имеют различную квалификацию.

Разрешение на сброс сточных вод может быть выдано только первому предприятию т.к. по данным обоих лаборантов концентрации вредного вещества находятся в допустимых пределах. Для разрешения второму обьекту необходимо проведение дополнительных исследований вследствие существенности статистического различия результатов, полученных лаборантами.

Так же, в процессе работы было определено количество проб, необходимое для анализа. При этом задавалось условие уменьшения предельной ошибки выборки в два раза: . Для примера был проведён расчёт для проб веществ из обоих предприятий, исследуемых первым лаборантом.

Всего для анализа с первого объекта для первого лаборанта было поставлено  проб, при этом предельная ошибка данной выборки составила . Было рассчитано, что для уменьшения данной ошибки в 2 раза необходимо поставить на анализ  проб.

Так же для анализа из второго объекта для первого лаборанта было поставлено  проб, при этом предельная ошибка данной выборки составила . Было рассчитано, что для уменьшения данной ошибки в 2 раза необходимо поставить на анализ  проб веществ.

 

Список использованной литературы

 

1. Легомина И. Н. Курс лекций по математическому моделированию ПТС.

2. Романов М. Ф., Федоров М. П. Математические модели в экологии. СПб 2003 г.

3. Гарин В. М., Клёнова И. А., Колесников В. И. Экология для технических вузов Серия «Высшее образование». Под ред. В. М. Гарина. Ростов н/Д:Феникс, 2003. — 384 с.

4. Попов А. М., Румянцев И. С. Природоохранные сооружения. — М.: Колос, 2005. — 520 с