2020-01-14
130
Наиболее употребляемыми в математической физике интегральными преобразованиями являются преобразования Лапласа, Фурье и Меллинга.
Пусть функция 
определена на полуоси 
. Ее преобразованием Лапласа называется функция
.(4)
Теорема 3. [7, c.113] Пусть функция непрерывна при 
и удовлетворяет оценке
(5)
Тогда ее преобразование Лапласа 
есть функция, регулярная в полуплоскости 
.
Доказательство. Воспользуемся следствием 1 из теоремы 1. Условия 2, 3 теоремы 1 выполнены. Пусть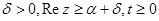 
. Тогда
.
Так как 
сходится, то по признаку Вейерштрасса интеграл (4) сходится равномерно по 
при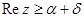 
и функция регулярна в этой полуплоскости. В силу произвольности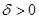 
функция регулярна при .
Преобразованием Фурье функции определенной на действительной оси, называется функция
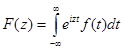(6)
Теорема 4. [7, c.113] Пусть функция непрерывна при 
и удовлетворяет оценкам
, (7)
где 
. Тогда ее преобразование Фурье 
есть функция, регулярная в полосе 
.
Доказательство. Разобьем интеграл (6) на два интеграла:
|
|
|
.
В силу условия (7) и теоремы 3 функция 
регулярна в полуплоскости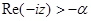 
, а функция 
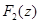- в полуплоскости 
, что и доказывает теорему.
В частности, если функция финитна, т.е.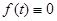 
при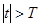 
, и непрерывна при 
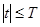, то ее преобразование Фурье является целой функцией. Это следует из теоремы 1, поскольку в этом случае
.
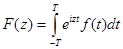Преобразованием Меллина функции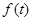 
, определенной на полуоси , называется функция
(8)
Здесь 
.
Теорема 5. [7, c.114] Пусть функция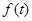 
непрерывна при 
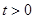и удовлетворяет оценкам:
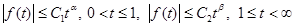, (9)
где 
. Тогда ее преобразование Меллина является функцией, регулярной в полосе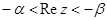 
.
Доказательство. Разобьем интеграл (8) на два интеграла
.
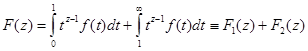Пусть 
, 
и 
; тогда
.
Так как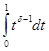 
сходится при 
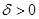, то, по признаку Вейерштрасса, интеграл 
сходится равномерно по 
при 
. В силу следствия 2 функция регулярна в полуплоскости 
.
Далее, при 
, 
и 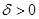имеем
Из сходимости интеграла 
и следствия 1 вытекает, что функция 
регулярна в полуплоскости 
.
Преобразования Фурье и Меллина связаны следующим соотношением:
, (10)
где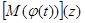 
- преобразование Меллина, а 
- преобразование Фурье функции 
. Действительно, делая замену переменной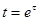 
, получаем
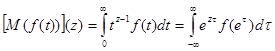
(мы предполагаем, что все интегралы сходятся). Последний интеграл совпадает с правой частью формулы (10).
В частности, с помощью соотношения (10) можно вывести теорему 5 из теоремы 4.
