Кафедра: Высшая математика
Реферат
По дисциплине «Высшая математика»
Тема: «Предел и непрерывность функций нескольких переменных»
Тольятти, 2008
Введение
Понятие функции одной переменной не охватывает все зависимости, существующие в природе. Даже в самых простых задачах встречаются величины, значения которых определяются совокупностью значений нескольких величин.
Для изучения подобных зависимостей вводится понятие функции нескольких переменных.
Понятие функции нескольких переменных
Определение. Величина u называется функцией нескольких независимых переменных (x, y, z, …,t), если каждой совокупности значений этих переменных ставится в соответствие определенное значение величины u.
Если переменная является функцией от двух переменных х и у, то функциональную зависимость обозначают
z = f (x, y).
Символ f определяет здесь совокупность действий или правило для вычисления значения z по данной паре значений х и у.
Так, для функции z = x 2 + 3 xy
при х = 1 и у = 1 имеем z = 4,
при х = 2 и у = 3 имеем z = 22,
при х = 4 и у = 0 имеем z = 16 и т.д.
Аналогично называется величина u функцией от трех переменных x, y, z, если дано правило, как по данной тройке значений x, y и z вычислить соответствующее значение u:
u = F (x, y, z).
Здесь символ F определяет совокупность действий или правило для вычисления значения u, соответствующего данным значениям x, y и z.
Так, для функции u = xy + 2 xz – 3 yz
при х = 1, у = 1 и z = 1 имеем u = 0,
при х = 1, у = -2 и z = 3 имеем u = 22,
при х = 2, у = -1 и z = -2 имеем u = -16 и т.д.
Таким образом, если в силу некоторого закона каждой совокупности п чисел (x, y, z, …,t) из некоторого множества Е ставится в соответствие определенное значение переменной u, то и u называется функцией от п переменных x, y, z, …,t, определенной на множестве Е, и обозначается
u = f (x, y, z, …,t).
Переменные x, y, z, …,t называются аргументами функции, множество Е – областью определения функции.
Частным значением функции называется значение функции в некоторой точке М 0 (x 0, y 0, z 0, …,t 0) и обозначается f (М 0) = f (x 0, y 0, z 0, …,t 0).
Областью определения функции называется множество всех значений аргументов, которым соответствуют какие-либо действительные значения функции.
Функция двух переменных z = f (x, y) в пространстве представляется некоторой поверхностью. То есть, когда точка с координатами х, у пробегает всю область определения функции, расположенную в плоскости хОу, соответствующая пространственная точка, вообще говоря, описывает поверхность.
Функцию трех переменных u = F (x, y, z) рассматривают как функцию точки некоторого множества точек трехмерного пространства. Аналогично, функцию п переменных u = f (x, y, z, …,t) рассматривают как функцию точки некоторого п -мерного пространства.
Предел функции нескольких переменных
Для того чтобы дать понятие предела функции нескольких переменных, ограничимся случаем двух переменных х и у. По определению функция f (x, y) имеет предел в точке (х 0, у 0), равный числу А, обозначаемый так:
 (1)
(1)
(пишут еще f (x, y) → А при (x, y) → (х 0, у 0)), если она определена в некоторой окрестности точки (х 0, у 0), за исключением, быть может, самой этой точки и если существует предел
 (2)
(2)
какова бы ни была стремящаяся к (х 0, у 0) последовательность точек (xk, yk).
Так же, как в случае функции одной переменной, можно ввести другое эквивалентное определение предела функции двух переменных: функция f имеет в точке (х 0, у 0) предел, равный А, если она определена в некоторой окрестности точки (х 0, у 0) за исключением, быть может, самой этой точки, и для любого ε > 0 найдется такое δ > 0, что
| f (x, y) – A | < ε (3)
для всех (x, y), удовлетворяющих неравенствам
0 <  < δ. (4)
< δ. (4)
Это определение, в свою очередь, эквивалентно следующему: для любого ε > 0 найдется δ-окрестность точки (х 0, у 0) такая, что для всех (x, y) из этой окрестности, отличных от (х 0, у 0), выполняется неравенство (3).
Так как координаты произвольной точки (x, y) окрестности точки (х 0, у 0) можно записать в виде х = х 0 + Δ х, у = у 0 + Δ у, то равенство (1) эквивалентно следующему равенству:

Рассмотрим некоторую функции, заданную в окрестности точки (х 0, у 0), кроме, быть может, самой этой точки.
Пусть ω = (ω х, ω у) – произвольный вектор длины единица (|ω|2 = ω х 2 + ω у 2 = 1) и t > 0 – скаляр. Точки вида
(х 0 + t ω х, y 0 + t ω у) (0 < t)
образуют луч, выходящий из (х 0, у 0) в направлении вектора ω. Для каждого ω можно рассматривать функцию
f (х 0 + t ω х, y 0 + t ω у) (0 < t < δ)
от скалярной переменной t, где δ – достаточно малое число.
Предел этой функции (одной переменной t)
 f (х 0 + t ω х, y 0 + t ω у),
f (х 0 + t ω х, y 0 + t ω у),
если он существует, естественно называть пределом f в точке (х 0, у 0) по направлению ω.
Пример 1. Функции

определены на плоскости (x, y) за исключением точки х 0 = 0, у 0 = 0. Имеем (учесть, что  и
и  ):
):

Отсюда

(для ε > 0 полагаем δ = ε/2 и тогда | f (x, y) | < ε, если  < δ).
< δ).
Далее, считая, что k – постоянная, имеем для y = kx равенство

из которого видно, что предел φ в точке (0, 0) по разным направлениям вообще различен (единичный вектор луча y = kx, х > 0, имеет вид
 ).
).
Пример 2. Рассмотрим в R 2 функцию
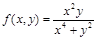 (х 4 + у 2 ≠ 0).
(х 4 + у 2 ≠ 0).
Данная функция в точке (0, 0) на любой прямой y = kx, проходящей через начало координат, имеет предел, равный нулю:
 при х → 0.
при х → 0.
Однако эта функция не имеет предела в точки (0, 0), ибо при у = х 2
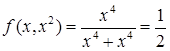 и
и 
Будем писать 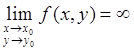 , если функция f определена в некоторой окрестности точки (х 0, у 0), за исключением, быть может, самой точки (х 0, у 0) и для всякого N > 0 найдется δ > 0 такое, что
, если функция f определена в некоторой окрестности точки (х 0, у 0), за исключением, быть может, самой точки (х 0, у 0) и для всякого N > 0 найдется δ > 0 такое, что
| f (x, y) | > N,
коль скоро 0 <  < δ.
< δ.
Можно также говорить о пределе f, когда х, у → ∞:
 (5)
(5)
Например, в случае конечного числа А равенство (5) надо понимать в том смысле, что для всякого ε > 0 найдется такое N > 0, что для всех х, у, для которых | x | > N, | y | > N, функция f определена и имеет место неравенство
| f (x, y) – А | < ε.
Справедливы равенства
 (6)
(6)
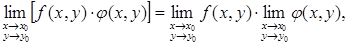 (7)
(7)
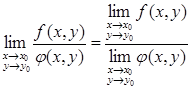
 (8)
(8)
где может быть х → ∞, у → ∞. При этом, как обычно, пределы (конечные) в их левых частях существуют, если существуют пределы f и φ.
Докажем для примера (7).
Пусть (xk, yk) → (х 0, у 0) ((xk, yk) ≠ (х 0, у 0)); тогда
 (9)
(9)
Таким образом, предел в левой части (9) существует и равен правой части (9), а так как последовательность (xk, yk) стремится к (х 0, у 0) по любому закону, то этот предел равен пределу функции f (x, y) ∙φ (x, y) в точке (х 0, у 0).
Теорема. если функция f (x, y) имеет предел, не равный нулю в точке (х 0, у 0), т.е.

то существует δ > 0 такое, что для всех х, у, удовлетворяющих неравенствам
0 <  < δ, (10)
< δ, (10)
она удовлетворяет неравенству
 (12)
(12)
Поэтому для таких (x, y)

т.е. имеет место неравенство (11). Из неравенства (12) для указанных (x, y) следует 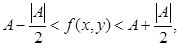 откуда
откуда  при A > 0 и
при A > 0 и  при
при
A < 0 (сохранение знака).
По определению функция f(x) = f (x 1, …, xn) = A имеет предел в точке
x 0 =  , равный числу А, обозначаемый так:
, равный числу А, обозначаемый так:

(пишут еще f(x) → A (x → x 0)), если она определена на некоторой окрестности точки x 0, за исключением, быть может, ее самой, и если существует предел

какова бы ни была стремящаяся к x 0 последовательность точек хk из указанной окрестности (k = 1, 2,...), отличных от x 0.
Другое эквивалентное определение заключается в следующем: функция f имеет в точке x 0 предел, равный А, если она определена в некоторой окрестности точки x 0, за исключением, быть может, ее самой, и для любого ε > 0 найдется такое δ > 0, что
 (13)
(13)
для всех х, удовлетворяющих неравенствам
0 < | x – x 0| < δ.
Это определение в свою очередь эквивалентно следующему: для любого ε > 0 найдется окрестность U (x 0 ) точки x 0 такая, что для всех х  U(x 0 ), х ≠ x 0, выполняется неравенство (13).
U(x 0 ), х ≠ x 0, выполняется неравенство (13).
Очевидно, что если число А есть предел f(x) в x 0, то А есть предел функции f(x 0 + h) от h в нулевой точке:

и наоборот.
Рассмотрим некоторую функцию f, заданную во всех точках окрестности точки x 0, кроме, быть может, точки x 0; пусть ω = (ω1,..., ω п) – произвольный вектор длины единица (|ω| = 1) и t > 0 – скаляр. Точки вида x 0 + t ω (0 < t) образуют выходящий из x 0 луч в направлении вектора ω. Для каждого ω можно рассматривать функцию
 (0 < t < δω)
(0 < t < δω)
от скалярной переменной t, где δω есть число, зависящее от ω. Предел этой функции (от одной переменной t)

если он существует, естественно называть пределом f в точке x 0 по направлению вектора ω.
Будем писать  , если функция f определена в некоторой окрестности x 0, за исключением, быть может, x 0, и для всякого N > 0 найдется δ > 0 такое, что | f(x) | > N, коль скоро 0 < | x – x 0| < δ.
, если функция f определена в некоторой окрестности x 0, за исключением, быть может, x 0, и для всякого N > 0 найдется δ > 0 такое, что | f(x) | > N, коль скоро 0 < | x – x 0| < δ.
Можно говорить о пределе f, когда х → ∞:
 (14)
(14)
Например, в случае конечного числа А равенство (14) надо понимать в том смысле, что для всякого ε > 0 можно указать такое N > 0, что для точек х, для которых | x | > N, функция f определена и имеет место неравенство 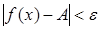 .
.
Итак, предел функции f(x) = f(x 1,..., хп) от п переменных определяется по аналогии так же, как для функции от двух переменных.
Таким образом, перейдем к определению предела функции нескольких переменных.
Число А называется пределом функции f(M) при М → М 0, если для любого числа ε > 0 всегда найдется такое число δ > 0, что для любых точек М, отличных от М 0 и удовлетворяющих условию | ММ 0 | < δ, будет иметь место неравенство | f(M) – А | < ε.
Предел обозначают  В случае функции двух переменных
В случае функции двух переменных 
Теоремы о пределах. Если функции f 1 (M) и f 2 (M) при М → М 0 стремятся каждая к конечному пределу, то:
а) 
б) 
в) 


Пример 1. Найти предел функции: 
Решение. Преобразуем предел следующим образом:

Пусть y = kx, тогда 
Пример 2. Найти предел функции: 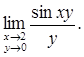
Решение. Воспользуемся первым замечательным пределом  Тогда
Тогда 
Пример 3. Найти предел функции: 
Решение. Воспользуемся вторым замечательным пределом  Тогда
Тогда 
 2020-01-15
2020-01-15 625
625







