Для восстановления аналогового сигнала по дискретному из построенного графика спектра сигнала необходимо выбрать количество значимых гармоник, позволяющих с заданной точностью восстановить сигнал. Обозначим его как mk. В данном случае mk = 3.
Исходя из этого, возможно восстановление сигнала, используя ряд Фурье:
x(t) =  (1.8)
(1.8)

Рис. 1.3. Восстановленный сигнал
Восстановление аналогового сигнала по теореме Котельникова
Расчет параметров
В 1933 г. В. А. Котельников доказал теорему, которая является одним из фундаментальных положений теоретической радиотехники и других областей. Эта теорема устанавливает возможность сколь угодно точного восстановления мгновенных значений сигнала исходя из отсчетных значений, взятых через равные промежутки времени.
Теорему Котельникова принято формулировать так: произвольный сигнал, спектр которого не содержит частот выше fв Гц, может быть полностью восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени  . Если же условия теоремы нарушаются и отсчеты во времени берутся недостаточно часто, то однозначное восстановление исходного сигнала принципиально невозможно.
. Если же условия теоремы нарушаются и отсчеты во времени берутся недостаточно часто, то однозначное восстановление исходного сигнала принципиально невозможно.
Физический смысл теоремы заключается в следующем. Пусть требуется передать значение непрерывной функции x(t) с интервалом времени dt. Чем короче dt, тем точнее будет передаваться функция.
Для восстановления АС по дискретному данным методом необходимо рассчитать следующие параметры:
1. ширина спектра сигнала:
Wm = 2mkw (1.9)
Учитывая формулу 1.2, получим:
Wm = 0.377 рад/с
2. интервал дискретизации рассчитывается по теореме Котельникова:
dt =  (1.10)
(1.10)
dt = 8.333 с
3. количество дискретных значений сигнала, подлежащих передаче по КС
Km  (1.11)
(1.11)
Km = 12
4. значения сигнала, подлежащие передаче по КС
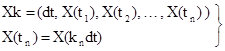 (1.12)
(1.12)

 2020-01-15
2020-01-15 293
293








