Векторна функція скалярного аргументу

Простішим способом задання просторової кривої є задання її векторним рівнянням

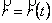, (7.19)

де - радіус – вектор точки кривої; - параметр, який визначає положення точки на кривій. Змінний вектор є функція скалярного аргументу ; такі функції в математичному аналізі називають векторними функціями скалярного аргументу.

Розкладемо вектор по осях координат. Рівняння просторової кривої (7.19) набуває вигляду

(7.20)

( - орти координатних осей). Звідси від векторного рівняння кривої можна перейти до її параметричного рівняння

. (7.21)

Це показує, що задання однієї векторної функції від скалярного аргументу рівнозначно заданню трьох скалярних функцій від того самого аргументу.

По відношенню до векторної функції (7.19), яка задає дану криву, сама крива називається годографом цієї векторної функції.

Розглянемо дві близькі точки кривої, заданої рівнянням (7.19): точку , відповідну значенню параметра , і точку , відповідну значенню параметра (рис.7.5).

Радіуси – вектори цих точок:

.

Вектор - називається приростом векторної функції , відповідним приросту її аргументу, і позначається

. (7.22)

Рис.7.7

 

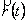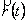Векторна функція - неперервна функція аргументу , якщо . Похідну від функції введемо так само, як у випадку скалярної функції: розділимо на і перейдемо до границі при ; якщо ця границя існує, то її назвемо похідною від векторної функції 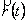за аргументом :

. (7.23)

Установимо напрямок вектора 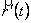. Зрозуміло, що вектор - колінеарний з вектором і при направлений в той самий бік, що і вектор , а при - в протилежний бік. У першому випадку , в другому - . Отже, вектор завжди направлений по січній годографа функції 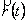в бік зростання параметра .

При сусідня точка кривої намагається співпасти з точкою і січна годографа в границі переходить в дотичну до нього. Тому вектор 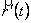направлений по дотичній до годографа в бік зростання параметра .

Якщо використати розклад (7.20) вектора 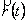за ортами, то вектор можна записати у вигляді

,

де

,

.

Звідси, поділивши на і перейшовши до границі при , знаходимо для похідної вектора такий вираз:

. (7.24)

Із означення похідної від векторної функції (7.23) можна вивести, що правила диференціального числення відносно диференціювання суми і добутку залишаються в силі як для сум векторних функцій, так і для добутків будь-якого вигляду. Мають місце такі формули:

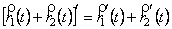; (7.25)

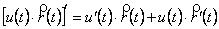; (7.26)

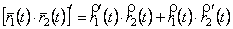; (7.27)

. (7.28)

Тут - векторні функції; - скалярна функція аргументу .

Зауваження. Розглянемо випадок змінного вектора 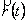, довжина якого стала: .

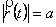Остання рівність дозволяє записати:

,

де 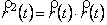- скалярний квадрат вектора .

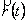Диференціюванням знаходимо

.

Отже, вектор 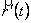в цьому випадку перпендикулярний до вектора .

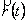Зокрема, якщо 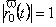, то .