Кривизна плоскої кривої

План

· Диференціал дуги

· Кривизна плоскої кривої

· Векторна функція скалярного аргументу

· Кривизна плоскої кривої

· Кривизна просторової кривої

· Кручення просторової лінії

· Формули Серре-Френе

Диференціал кривої

Поняття довжини кривої буде розглянуто в розділі інтегрального числення. Криві, для яких можна установити поняття довжини, називають в математичному аналізі спрямними.

Умова спрямності кривої для плоскої кривої, заданої параметричними рівняннями , полягає в такому: на спрямному відрізку кривої функції і мусять мати неперервні похідні за параметром : 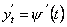. Аналогічною є умова спрямності просторової кривої, заданої рівняннями ; вона полягає в неперервності похідних .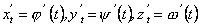

Для всякої спрямної кривої як просторової, так і плоскої, наслідком її спрямності є така геометрична властивість: границя відношення нескінченно малої дуги кривої до стягуючої її хорди дорівнює одиниці за умови, що хорда стикується в точку.

Якщо довжину малої дуги кривої позначити через , а довжину відповідної хорди – через (рис. 7.4), то

(7.4)

Виходячи саме з цієї властивості, знайдемо вирази для диференціала дуги як плоскої, так і просторової кривої.

На плоскій спрямній кривій, рівняння якої ,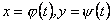

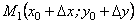візьмемо дві сусідні точки. та , що

відповідають значенням параметра та (рис. 7.2).

Довжина хорди знаходиться за формулою

(7.5)

Похідна від довжини дуги кривої за параметром :

.

Замінимо його виразом за формулою (7.5):

.

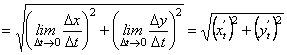Отже,

. (7.6)

Звідси

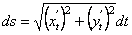. (7.7)

Якщо крива задана рівнянням , то можна прийняти за параметр кривої: .

Диференціал дуги

Якщо крива задана рівнянням в полярних координатах 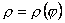, то за параметр кривої можна прийняти полярний кут .

Диференціюємо по рівності

Маємо

.

Звідси

,

тому

. (7.9)

Рис.7.4 Рис.7.5

Приклади.

1. Знайти диференціал дуги циклоїди

.

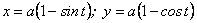Р о з в ’ я з о к. .

.

2. Знайти диференціал дуги кардіоїди .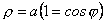

Р о з в ’ я з о к. ,

.

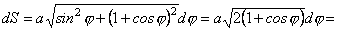
Диференціал дуги просторової кривої, заданої параметричними рівняннями , можна знайти аналогічно.

Відміна від попереднього полягає лише в тому, що довжина хорди, яка з’єднує точки просторової кривої і визначається за формулою

.

Формула диференціала дуги просторової кривої

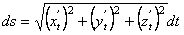. (7.10)

Приклад. Знайти диференціал дуги гвинтової лінії:

.

Р о з в ’ я з о к. .

.

Формулам (7.9) і (7.10) часто надають такого вигляду:

(для плоскої кривої); (7.11 (для просторової кривої); (7.12)

Диференціал дуги плоскої кривої має такий геометричний зміст: він дорівнює довжині відрізка дотичної до кривої (рис.7.5).

Кривизна плоскої кривої

Вивчаючи ту чи іншу криву, бачимо, що в різних точках вона має неоднаковий ступінь викривлення. Так, парабола поблизу початку координат більше викривлена, ніж в точках, які знаходяться далі від початку координат. Коло в усіх своїх точках має однакове викривлення. Різні криві також відрізняються одна від одної своїм ступенем викривлення. Коло малого радіуса більше викривлено, ніж коло великого радіуса.

Виникає запитання: що ж брати за міру кривизни кривої в її окремих точках? Щоб відповісти на нього, припустимо, що до кривої в кожній точці можна провести дотичну і що крива є спрямлюваною.

Візьмемо на кривій дві точки і (рис. 7.6) і в цих точках проведемо дотичні прямі. Нехай дотична утворює з додатним напрямом осі кут , а пряма - кут .

Довжину дуги позначимо . Модуль відношення , де - величина кута в радіанах, на який повертається дотична, коли точка переміститься вздовж кривої в точку , називається середньою кривизною дуги .

Рис.7.6

Означення. Границя (якщо вона існує) середньої кривизни дуги даної кривої, коли точка наближається вздовж кривої до точки , називається кривизною кривої в точці і позначається

. (7.13)

Виведемо формулу для обчислення кривизни. Нехай крива задана в декартовій системі координат рівнянням

,

де функція 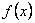на відрізку має похідні до другого порядку включно.

Скористаємося формулою (7.13). Очевидно, що коли точка , то довжина дуги . Тому формулу (7.13) можна

записати ще так:

. (7.14)

З другого боку, якщо - кут, утворений дотичною до кривої в точці з додатним напрямом осі , то

.

Звідси

.

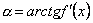Тоді

.

Підставляючи в формулу (7.14) значення і значення , дістаємо формулу для кривини кривої:

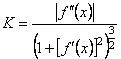. (7.15)

З цієї формули легко дістати формулу для кривизни кривої,

коли остання задана параметричними рівняннями . Справді,

,

.

Тоді, підставляючи значення у формулу (7.15), маємо

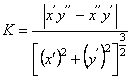. (7.16)

Якщо крива задана в полярній системі координат рівнянням , то

. (7.17)

Величину, обернену до кривої в заданій точці, називають радіусом кривизни кривої і позначають через :

. (7.18)

Коло, яке з даною кривою має в даній точці спільну дотичну, спільну кривизну і однаковий напрямок вгнутості, називається колом кривизни, а його центр – центром кривизни кривої в даній точці. Радіус кола кривизни

.

Для всіх плоских кривих (за винятком кола) центри кривизни різні в різних точках кривої. Геометричне місце центрів кривизни даної кривої називається її еволютою, а сама крива по відношенню до еволюти називається евольвентою.