Глава II. Полиномы Лагерра

В математике, многочлены Лагерра, названные в честь Эдмона Лагерра (1834—1886), являются каноническими решениями Уравнения Лагерра:

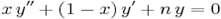
являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра, обычно обозначающиеся как , являются последовательностью полиномов, которая может быть найдена по Формуле Родрига

Эти полиномы ортогональны друг другу со скалярным произведением:

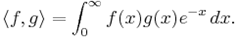
Многочлены Лагерра применяются в квантовой механике, в радиальной части решения уравнения Шредингера для атома с одним электроном. Имеются и другие применения многочленов Лагерра.

Полиномы Лагерра можно определить рекуррентной формулой:

предопределив первые два полинома как:

Обобщенные полиномы Лагерра.

где:

· **— главное (радиальное) квантовое число;

· ^***— орбитальное (азимутальное) квантовое число.

Обобщённые полиномы Лагерра являются решениями уравнения:

так что .

ГлаваIII. Применение полиномов Лагерра в квантовой

механике.

 Многочлены Лагерра нашли свое применение в квантовой механике: