Случай наличия кратных корней характеристического уравнения

ЛИНЕЙНЫЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

I. МЕТОД ЭЙЛЕРА

 

211. Предварительные замечания. В этой главе мы будем изучать линейные системы уравнений:

  

 

 

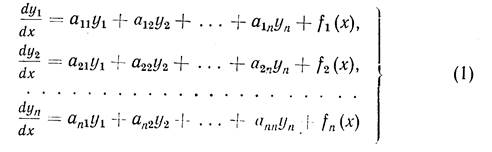
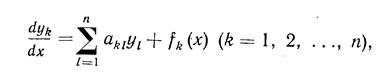
Или                                                                                                            (1′)                                                                                                                                                                                                                              

 

 

Где коэффициенты a_kl=(k, l=1,2,…,n) – постоянные вещественные числа, а f_k(x) (k=1,2,…,n) – функции от х, непрерывные в интервале (a,b).

Применяя общую теорию линейных систем уравнений, изложенную в предыдущей главе, мы покажем, что система (1) всегда может быть проинтегрирована в конечном виде, т. е. либо в элементар- ных функциях, либо в квадратурах.

Так как интегрирование неоднородной линейной системы приводится к интегрированию соответствующей однородной си­стемы, то рассмотрим сначала вопрос о построении общего решения однородной системы:

 

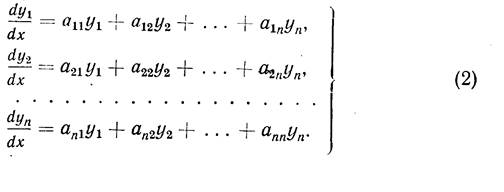
В силу теоремы о построении общего решения, для построения общего решения системы (2) достаточно построить хоть одну фундаментальную систему решений.

Применяя теорему о существовании фундаментальной системы решений, мы видим, что существует фунда­ментальная система решений, определенных и непрерывных в промежутке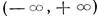

Более того, согласно замечанию теоремы о существовании фундаментальной системы решений, существует фундаментальная система решений, голо­морфных в интервале  .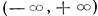

Мы покажем, что фундаментальная система решений может быть построена из элементарных функций, голоморфных в интервале .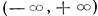

 

212. Построение фундаментальной системы решений и об­щего решения однородной линейной системы в случае различ­ных корней характеристического уравнения. По аналогии с однородным линейным уравнением с постоянными коэффици­ентами будем искать частное решение системы (2) в виде

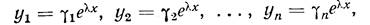          (3)

g₁, g₂,..,g_n  и  l - некоторые постоянные числа, причем числа g₁, g₂,..,g_n не равны нулю одновременно, ибо в про­тивном случае мы получили бы очевидное нулевое решение, которое не может входить в состав фунда- ментальной системы и, следовательно, не может быть использовано для построения общего решения.

Обратим особое внимание на то, что число lмы берем одно и то же для всех функций, составляющих решение.

Подставляя функции (3) в систему (2), сокращая на е^lx  и пере- нося все члены направо, получим для определения чи­сел g_k следующую систему: 

                

 

 

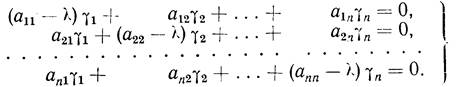
(4)

 

Нас интересует ненулевое решение этой системы. Такое решение существует лишь при условии, что определитель си­стемы равен нулю, т. е. при условии

  

 

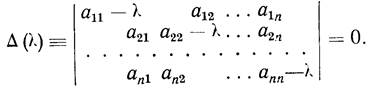
                                           (5)                                                                                     

                                                                                                            

 

 Уравнение (5) называется характеристическим уравнением системы

(2), его корни— характеристическими числами, а оп­ределитель D(l) - характеристическим определителем.

Рассмотрим сначала случай, когда все характеристические числа    

l₁,l₂,...,l_n   различны. В этом случае имеем: D(l_i)=0, но 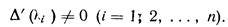  Вследствие этого ранг матрицы

 

Составленной из коэффициентов системы

 

 

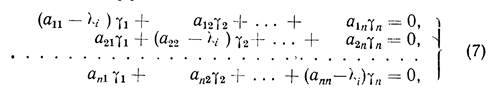
которая получается из системы (4) после замены в ней l на l _i  - равен n-1.

Действительно, вычисляя D’(l), имеем:  

 

 

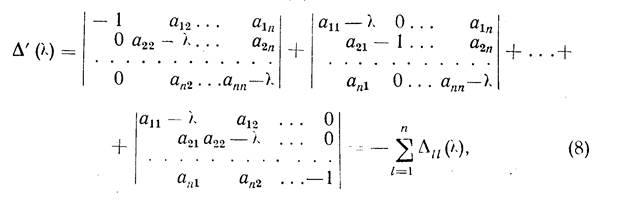
где D _ll (l) - алгебраическое дополнение элемента a _ll - l определителя D(l). Так как 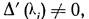 то из (8) видим, что хоть один из определи- телей (п —1)-го порядка, именно один из D _ll (l _i), отличен от нуля, так что ранг рассматриваемой матрицы ра­вен п — 1.

Поэтому одно из уравнений системы (7) есть следствие осталь-ных и эта система имеет ненулевое решение, определен­ное с точ-ностью до произвольного множителя пропорциональ­ности A _i:

g _i1 = A_im_i1, g _i2 = A_im_i2,…, g _in = A_im_in(i =1.2,…, n). (9)

Например, в качестве g _ik можно взять алгебраические до­полнения элементов любой строки определителя D _l (l _i), если не все они равны нулю. В самом деле, так как сумма произведе­ний элементов какой-либо строки определителя D _l (l _i) на алге­браические дополнения эле-ментов другой строки равна нулю, а сумма произведений элементов строки на их алгебраические дополнения равна самому определителю D(l _i)т. е. снова равна нулю, то ясно, что, заменив в системе (7) неизвестные g _k взя­тыми алгебраическими дополнениями, мы получим тождества.

Фиксируя в формулах (9) множитель A _i, мы получим определен-ное решение системы (7).

Подставляя теперь в (3) вместо lпоследовательно характе­ристи-ческие числа  l _i,а вместо g₁, g₂,..., g_n— соответствующие им решения системы (7), определяемые формулами (9) при фиксированных множителях A _i, получим п решений:

 

 

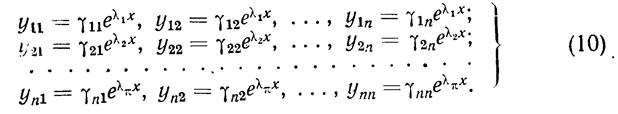
Эти решения линейно независимы в интервале .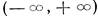

Если при этом все корни l₁, l₂,..., l_n  вещественны, то все решения (10) тоже будут вещественными.

Таким образом, в случае различных вещественных корней характеристического уравнения система (2) имеет п веществен­ных линейно независимых частных решений вида (10), так что последние образуют фундаментальную систему решений.

Поэтому, в силу теоремы о построении общего решения, формулы

 

 

Дают общее решение системы (2) в области

 

 

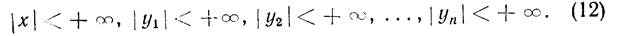
Если характеристические числа различные, но среди них есть комплексные, то последние входят сопряженными парами. Пусть       a + ib и а – ib — простые корни характеристического уравнения. Корню a+ib соответствует согласно формуле (3) решение

y₁=g₁ e ^{( a+ib)x}, y₂=g₂ e ^{( a+ib)}, …, y _n =g _ne ^{( a+ib)}.                     (13)

здесь g1,g2,...,g n – комплексные числа. Полагая

       g₁=g₁₁+ i g₂₁, g₂=g₁₂+ i g₂₂, …,g _n =g_{1 n} + i g_{2 n},

Получаем решение

y₁=(g₁₁+ i g₂₁) e ^{( a+ib)x}, y₂=(g₁₂+ i g₂₂) e ^{( a+ib)x}, …, y _n =(g_{1 n} + i g_{2 n}) e ^{( a+ib)x}.

Это решение комплексное. Отделяя в нем вещественные и мни­мые части, мы получим, согласно свойствам решений однородной системы, два вещественных решения:

 

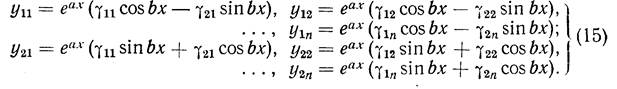
Эти решения, очевидно, линейно независимы в интервале 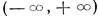. Нетрудно убедиться, что сопряженный корень а — ib не порождает новых вещественных линейно независимых частных решений.

Таким образом, если все характеристические числа — раз­личные и вещественные, то мы получаем соответствующие им вещественные линейно независимые частные решения в виде (10). Если же все характеристические числа — различные, но среди них есть комплексные, то последние обязательно входят сопряженными парами и каждой паре таких характеристиче­ских чисел соответствуют два линейно независимых частных решения вида (15). Всего мы получим п вещественных частных решений. Все эти решения линейно независимы в интервале .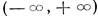

В самом деле, предположим обратное. Тогда, написав соответствующую систему соотношений между этими решениями и перейдя в ней от тригонометрических функций к 'показатель­ным, мы получили бы, что системы функций вида (10), где l ₁, l ₂, …, l _n —различные числа, оказались бы линейно зависимы­ми.

Общее решение системы (2) в области (12) представляет собою линейные комбинации построенных п вещественных ли­нейно независимых частных решений с произвольными посто­янными коэффициентами.

 

Пример 1. Найти общее решение системы:

 

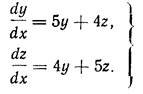
Решая характеристическое уравнение

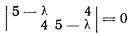         или      l²-10l+9=0;

находим: l₁=1, l₂=9, так что характеристические числа различные и ве­щественные.

Составляем систему для определения чисел g₁ и g₂соответствующих характеристическому числу l₁ = 1. Матрица коэффициентов этой системы получается из матрицы

 

5-l 4   

4 5-l      заменой l на l₁=1, так что искомая система будет иметь вид

 

                 

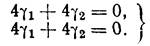
Здесь, как и следовало ожидать, второе уравнение является следствием первого (оно даже совпадает с первым уравнением) и его можно было и не выписывать. Полагая, находим g₁=1, находим g₂= −1

Таким образом, характеристическому числу Х₁=1 соответствует реше­ние:

y₁= е^х, z₁ = −e^x.                    (20)

Аналогично, решая систему, соответствующую характеристическому числу l₂=9:

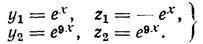                                    (21)

находим: g₁=1, g₂=1 так что этому характеристическому числу соот-ветствует решение:

y₂= e ^{9 x}, z₂=e^9x                         (22)

Мы получили фундаментальную систему решений:

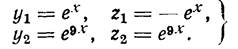(23)

 

Беря линейную комбинацию, получаем общее решение:

                     

 

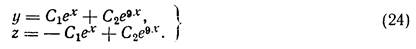
Пример 2. Рассмотрим систему:

         

 

Характеристическое уравнение

 

 

 

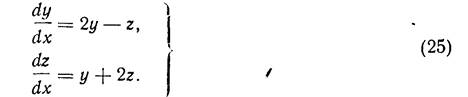
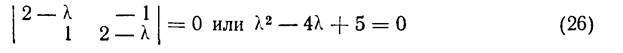
Имеет комплексные сопряженные корни λ₁ = 2 + i, λ₂ = 2 – i. Найдем решение, соответствующее λ_1. Это решение имеет вид y = γ₁e^(2+i)x,

z = γ₂e^(2+i)x. Числа γ₁ и γ₂ ищем из системы

   

 

Полагая γ₁=1, находим γ₂ = - i, так что искомым решением будет

 

 

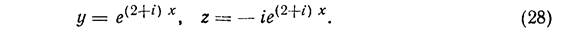
Это решение комплексное. Отделяя в нем вещественные и мнимые части, получим два вещественных решения

 

 

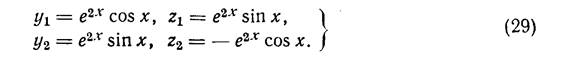
Эти решения составляют фундаментальную систему решений, так что общим решением будет

 

 

 

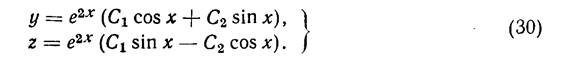
Пример 3. Найти общее решение системы:

Характеристическое уравнение

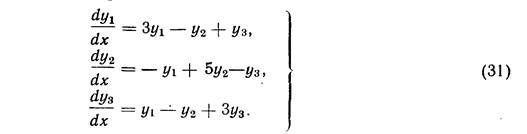
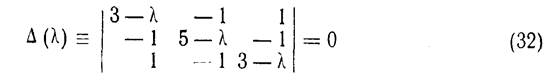
Имеет различные и притом вещественные корни λ₁ = 2, λ₂ = 3, λ₃=6, так что фундаментальная система решений имеет вид (10). Найдем сначала частное решение вида

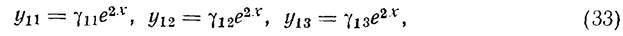
Соответствующее характеристическому числу λ₁ = 2. В качестве чисел γ_11, γ_22, …, γ_1n можно взять алгебраические дополнения элементов первой строки определителя

                        

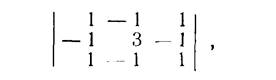
который получается из характеристического определителя Δ (λ) заменой λ на λ₁=2. Получаем

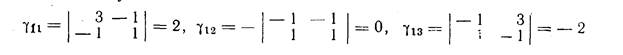
или (деля на 2)

 

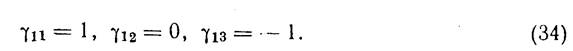
Подставляя эти значения γ_1k в (33), получим

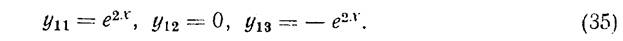
Аналогично найдем, что в качестве чисел γ_2k, γ_3k, соответствующих характеристическим числам λ₂ = 3, λ₃=6, можно взять γ₂₁ = 1, γ₂₂ = 1, γ₂₃ = 1, γ₃₁ = 1, γ₃₂ = -2, γ₃₃ = 1. Фундаментальной системой решений будет

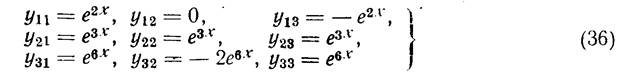
Так что общее решение имеет следующий вид

 

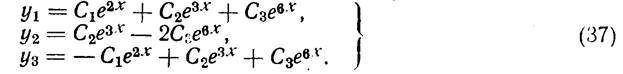
Случай наличия кратных корней характеристического уравнения.

  Если среди корней характеристического уравнения имеются кратные корни, то изложенный выше способ построе­ния фундаментальной системы решений, очевидно, не приме­ним.

Однако и в этом случае удается построить фундаменталь­ную систему решений в элементарных функциях.

Заметим, прежде всего, что если l₁есть простое характе­ристическое число, то независимо от того, будут среди осталь­ных характеристических чисел встречаться кратные или нет, ему всегда соответствует одно частное решение вида:

                  y₁=g₁e^l1x, y₂=g₂e^l1x, …, y_n=g_ne^l1x     (38)

где g₁, g₂, …,g_n — некоторые постоянные числа, определяемые с точностью до постоянного множителя.

Таким образом, задача сводится к тому, чтобы найти част­ные решения, соответствующие кратному корню.

При этом, так же как и для линейного однородного урав­нения n-го порядка, оказывается, что одному характеристичес­кому числу кратности k соответствует k линейно независимых частных решений.

Теорема. Если l₁ есть характеристическое число крат­ности k, то ему соответствует решение вида

y₁=P₁(x) e^l1x, y₂=P₂(x) e^l1x, …, y_n=P_n(x) e^l1x                                             (39)

где P₁(x), P₂(x), …, P_n(x) суть полиномы от х степени не вы­ше чем k−1, имеющие в совокупности k произвольных коэф­фициентов, так что среди всех коэффициентов всех этих поли­номов k коэффициентов являются произвольными, а все осталь­ные выражаются через них.

В частности может случиться, что все эти полиномы вырождаются в постоянные числа. В таком случае k-кратному харак­теристическому числу l₁ будет соответствовать решение вида

y₁=g₁e^l1x, y₂=g₂e^l1x, …, y_n=g_ne^l1x           (40)

Однако здесь k из коэффициентов g₁, g₂, …, g_n являются про­извольными, в то время как для простого характеристического числа произвольным является только один из них.

Практически при нахождении решения, соответствующего характеристическому числу l ₁ нужно искать решение в виде (39), считая P₁(х), Р₂(х),..., Р_п(х) полиномами (k−1)-й сте­пени с неопределенными коэффициентами и, подставляя (39) в (2), выразить все коэффициенты через k из них, которые оста­ются произвольными.

Полагая поочередно один из этих произвольных коэффици­ентов равным единице, а остальные равными нулю, мы построим k линейно независимых решений, соответствующих характеристическому числу l₁. Все эти частные решения будут состав­лены из произведений показательной функции e^l1x на полино­мы от х, степени которых не превышают k−1. Если же поли­номы в формулах (39) вырождаются в постоянные числа, то мы получим k линейно независимых частных решений такого же вида, как и в случае простого корня характеристического уравнения.

Если l₁ — вещественное характеристическое число, то по­строенные выше k линейно независимых решений будут веще­ственными.

Если же система (2) имеет комплексное характеристическое число a + ib кратности k, то оно имеет сопряженное характери­стическое число а — ib той же кратности.

Построив k линейно.независимых комплексных решений, со­ответствующих характеристическому числу a + ib, и отделив в них вещественные и мнимые части, мы получим 2k, веществен­ных линейно независимых частных решений.

В общем случае каждому простому вещественному характе­ристическому числу соответствует одночастное решение, каждой паре простых сопряженных комплексных характеристических чисел соответствует два вещественных линейно независимых решения, вещественному характеристическому числу кратности k соответствует k вещественных линейно независимых частных решений, а каждой паре сопряженных комплексных характе­ристических чисел кратности k соответствует 2k вещественных линейно независимых частных решений. Всего получается п вещественных решений. Все эти решения линейно независимы в интервале(-∞,+∞), так что они образуют фундаменталь­ную систему решений. Взяв линейные комбинации решений этой фундаментальной системы по столбцам с одними и теми же произвольными постоянными С₁, С₂,..., С_п, мы получим общее решение системы (2) в области (12).

 

Заметим, однако, что мы не можем,на основании указанной теоремы выяснить до конца структуру фундаментальной систе­мы решений до тех пор, тюка не построим ее фактически.

Мы выясним эту структуру в следующей главе, где будет дан другой способ построения фундаментальной системы, при­чем в отличие от настоящего пункта там строится сразу вся фундаментальная система.

Указанный выше вид фундаментальной системы решений дает возможность сделать некоторые заключения об устойчи­вости нулевого решения однородной системы (2)*.