2020-01-15
267
Обозначим через х точное (истинное) значение некоторой величины (точное число), а через а ее приближенное значение (приближенное число).
Число 
называется абсолютной погрешностью приближенного числа а.
Обычно абсолютная погрешность числа а неизвестна, так как не дано точное значение х, а известна так называемая предельная абсолютная погрешность. Число 
называется предельной абсолютной погрешностью приближенного числа а, если
Относительной погрешностью d приближенного числа а называется отношение абсолютной погрешности этого числа к абсолютной величине точного числа х:
.
Иногда в качестве относительной погрешности принимают величину 
, где - предельная абсолютная погрешность.
Если точное значение числа х неизвестно, а 
мало по сравнению с | а |, то можно считать, что
.
Относительную погрешность часто выражают в процентах, т. е.
.
Цифра данного разряда приближенного числа а называется верной, если абсолютная погрешность 
этого числа не превосходит пяти единиц следующего справа разряда. В противном случае эта цифра называется неверной.
Для всякого десятичного числа 
существует первая слева цифра, отличная от нуля. Эта цифра называется первой значащей цифрой числа а. Все цифры, начиная с первой значащей и правее, являются значащими цифрами числа а. Говорят, что приближенное число а имеет п верных значащих цифр, если его п -я и предшествующие ей значащие цифры верные, а (п + 1)-ая цифра - неверная.
В вычислительной практике также употребляют термин "число верных десятичных знаков" - под ним понимают число верных цифр в десятичной дроби после нулей, указывающих разряды. Цифры приближенного числа, не являющиеся верными, отбрасывают, а число при этом округляют.
Правило округления. Если первая из отбрасываемых цифр, считая слева направо, больше 5, то последнюю оставшуюся цифру надо увеличить на единицу.
Если отбрасывается только цифра 5, а предшествующая ей цифра четная, то последнюю оставшуюся цифру менять не следует если - нечетная, то последнюю оставшуюся цифру надо увеличить на единицу (правило четных знаков).
Пример, 
Округляя число до трех значащих цифр, получим 
, округляя его до четырех значащих цифр, получим 
, а округляя его до пяти значащих цифр, получим 
.
Окончательные результаты вычислении обычно округляют на последней верной цифре, а в промежуточных результатах удерживают одну запасную цифру, которая может оказаться и неверной.
При этом пользуются следующими правилами определения верных цифр результата:
1. При сложении (вычитании) приближенных чисел в сумме следует сохранить столько десятичных знаков, сколько их имеет слагаемое с наименьшим числом десятичных знаков;
2. При умножении приближенных чисел в произведении следует оставлять столько значащих цифр, сколько их имеет сомножитель с наименьшим числом верных значащих цифр;
3. При возведении в степень и извлечении корня число верных значащих цифр результата равно числу верных значащих цифр основания степени;
4. (Правило запасной цифры). Для того, чтобы в результате небольшого количества алгебраических действий над приближенными числами получить результат с п верными цифрами, достаточно исходные данные взять с (п + 1) верными цифрами и во всех промежуточных результатах сохранять (n +1) верных цифр, а окончательный результат округлить до п цифр.
Пример 1. Найти сумму S = 54,70 + 386,358 + 32,4357, предполагая, что все слагаемые выписаны с верными цифрами.
Последний верный разряд суммы - разряд сотых (см. первое слагаемое). Два остальных числа округляем на разряде тысячных (правило 4).
54,70 + 386,358 + 32,4357 = 473,494
Окончательный результат - 473,49 (правило 1).
Пример 2. Найти произведение 82,246 и 7,48. Второй сомножитель содержит наименьшее число верных значащих цифр (три). Поэтому первый сомножитель округляем до 82,25 (правило 4).
Производим умножение 82,25 7,48 = 615,2300. Результат округляем 615,23 (правило 2).
Применяя приведенные выше правила, следует иметь в виду, что они не дают гарантии точности последней цифры результата. При большом числе операций результат может иметь погрешность, достигающую даже нескольких единиц. Но при небольшом числе действий более вероятны малые значения этой погрешности.
Вычислительную работу по возможности следует упрощать. Для этого нужно пользоваться калькуляторами, электронными вычислительными машинами, а также математическими таблицами степеней, корней, обратных чисел (например, В. М. Брадис. Четырехзначные математические таблицы, любой год издания). Всякая вычислительная работа должна контролироваться. Простейшим методом контроля является выполнение решения заново (лучше спустя некоторое время) и сверка полученных результатов.
Основные правила приближенных вычислений будут нужны и в дальнейшем - при выполнении контрольных работ по высшей математике, теории вероятностей, математической статистике, математическому программированию и многим специальным дисциплинам.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1 "ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ"
Перед выполнением контрольной работы № 1 необходимо изучить и закрепить с помощью примеров для самостоятельной работы (см. рабочую программу) такие разделы и понятия как определители и их свойства; способы вычисления определителей второго и третьего порядков; алгебраические дополнения элемента определителя; вычисление определителей 4-го и более высоких порядков с помощь ю свойств определителя; матрицы и основные операции над ними, понятие обратной матрицы; элементарные преобразования над элементами строк (столбцов) матрицы; ранг матрицы и способы его вычисления; теорема Кронекера - Капелли; методы решения систем линейных алгебраических уравнений.
Литература: /1/ гл. 1 §1.1-1.6; гл. 2 § 2.1-2.5;
/3/ гл. 4 § 1, 2, 4-7.
ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА
Задание 1. Для данного определителя 
найти миноры и алгебраические дополнения элементов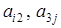 
. Вычислить определитель 
: а) разложив его по элементам i -ой строки; б) разложив его по элементам j -го столбца; в) получив предварительно нули в i -ой строки.
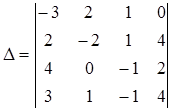i = 1, j = 2
Решение: 1. Находим миноры к элементам 
:
Алгебраические дополнения элементов 
соответственно равны:
2. а). Вычислим определитель, разложив его по элементам первой строки:
б) Вычислим определитель, разложив его по элементам второго столбца:
в) Вычисли определитель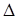 
, получив предварительно нули в первой строке. Используем свойство определителей: определитель не изменится, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на (-2) и прибавим ко второму. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом определитель по элементам первой строки и вычислим его:
В определителе третьего порядка получили нули в первом столбце по свойству тому же свойству определителей.
Задание 2. Даны две матрицы A и B. Найти: а) AB; б) BA; в) 
; г)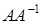 
.
Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле 
. Имеем:
б) Вычислим
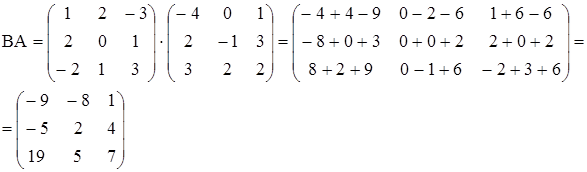
Очевидно, что 
;
в) Обратная матрица 
матрицы А имеет вид
где 
,
т.е. матрица A - невырожденная, и, значит, существует матрица . Находим:
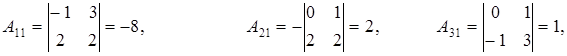
Тогда
;
г) Имеем:
;
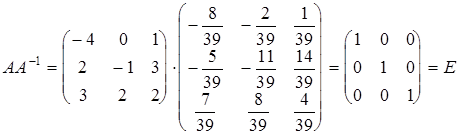Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера - Капелли. С помощью элементарных преобразований найдем ранг матрицы
данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим
.
Следовательно, 
(т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.
а) По формулам Крамера
,
где
,
,
,
,
находим: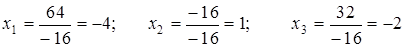 
.
б) Решим систему методом Гаусса. Исключим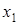 
из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:
Из полученной системы находим 
.
Задание 4. Проверить совместность линейной системы уравнений и в случае совместности решить ее: а) по формулам Крамера; б) методом Гаусса.
Решение: Проверяем совместность системы с помощью теоремы Кронекера - Капелли. В расширенной матрице
меняем третий и первый столбцы местами, умножаем первую строку на 3 и прибавляем ко второй, умножаем первую строку на 2 и прибавляем к третьей, из второй строки вычитаем третью:
.
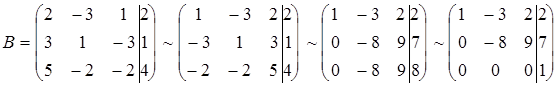Теперь ясно, что 
. Согласно теореме Кронекера - Капелли, из того, что 
следует несовместность исходной системы.
Задание 5. Решить однородную систему линейных алгебраических уравнений.
Решение: Определитель системы
,
поэтому система имеет единственное нулевое (тривиальное) решение: 
Задание 6. Решить однородную систему линейных алгебраических уравнений.
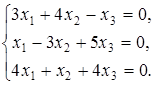
Решение: Так как определитель системы
,
то система имеет бесчисленное множество решений. Поскольку 
, 
, возьмем любые два уравнения системы (например, первое и второе) и найдем ее решение. Имеем:
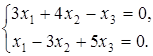
Так как определитель из коэффициентов при неизвестных 
и 
не равен нулю, то в качестве базисных неизвестных возьмем 
и (хотя можно брать и другие пары неизвестных) и переместим члены с 
в правые части уравнений:
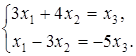
Решаем последнюю систему по формулам Крамера:
где
,
,
.
Отсюда находим, что 
Полагая 
, где k— произвольный коэффициент пропорциональности (произвольная постоянная), получаем решение исходной системы: 
.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 2 "ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ. ВЕКТОРЫ"
Перед выполнением контрольной работы № 2 необходимо изучить такие разделы и понятия высшей математики как прямоугольная декартова система координат, полярная система координат, векторы, линейные операции над векторами, проекция вектора на ось, деление отрезка в заданном отношении, скалярное, векторное и смешанное произведение векторов, прямая на плоскости и в пространстве, плоскость в пространстве, понятие линии на плоскости и в пространстве, кривые второго порядка, понятие поверхности в пространстве, поверхности второго порядка, линии, заданные уравнениями в полярной системе координат и параметрически.
Литература: /1/ гл. 3 §3.1-3.4, 3.6, 3.7; гл. 4 § 4.1-4.5, 4.7;
/2/ § 3-5;
/3/ гл. 1 § 1-3.
ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА
Задание 1. Даны векторы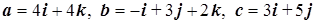 
.
Необходимо: а) вычислить смешанное произведение трех векторов a, b, 5 c; б) найти модуль векторного произведения векторов 3 c, b; в) вычислить скалярное произведение двух векторов a, 3 b; г) проверить, будут ли коллинеарными или ортогональными два вектора a, b; д) проверить, будут ли компланарны три вектора a, b, c.
Решение:
а) Так как 
, то
б) Поскольку 
, то
.
в) Находим: 
г) Так как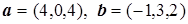 
и 
, то векторы 
и 
не коллинеарны. Поскольку 
, то векторы 
и не ортогональны;
д) векторы a, b, c компланарны, если их смешанное произведение равно нулю, т.е.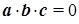 
. Вычисляем
,
т. е. векторы a, b, c не компланарны.
Задание 2. Даны вершины треугольника 
. Найти:
а) уравнение стороны АВ;
б) уравнение высоты СН;
в) уравнение медианы АМ;
г) точку N пересечения медианы AM и высоты СН;
д) уравнение прямой, проходящей через вершину C параллельно стороне AB;
е) расстояние от точки C до прямой AB.
Решение:
а) Воспользовавшись уравнением прямой, проходящей через две точки
,
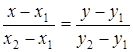получим уравнение стороны АВ:
.
откуда
или 
.
б) Используя уравнение прямой
найдем угловой коэффициент прямой АВ
Тогда 
. С учетом условия перпендикулярности прямых АВ и СН (
) угловой коэффициент высоты СН: 
.
Используя уравнение прямой проходящее через точку с угловым коэффициентом
составим уравнение высоты СН. По точке С (2, 7) и угловому коэффициенту составляем уравнение высоты СН:
или 
.
в) По формулам координат середины отрезка
находим координаты х, у середины М отрезка ВС:
.
Теперь по двум известным точкам A и М составляем уравнение медианы AM:
или 
.
г) Для нахождения координат точки N пересечения медианы AM и высоты СН составляем систему уравнений
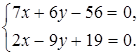
Решая ее, получаем 
;
д) Так как прямая, проходящая через вершину С, параллельна стороне АВ, то их угловые коэффициенты равны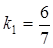 
. Тогда, согласно уравнению
,
по точке С и угловому коэффициенту 
составляем уравнение прямой CD:
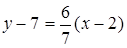или 
.
е) Расстояние от точки С до прямой АВ вычисляем по формуле:
.
Тогда
.
Построим координаты вершин треугольника, все точки и прямые найденные при решении данной задачи в прямоугольной системе координат (рис. 1).
 |
Задание 3. Составить канонические уравнения:
а) эллипса; большая полуось которого равна 3, а фокус находится в точке F (
, 0). Т.е. a = 3, F (, 0).
б) гиперболы с мнимой полуосью, равной 2, и фокусом F (- 
, 0). Т.е. b = 2, F (- 
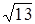, 0).
в) параболы, имеющей директрису x = - 3. Т.е. D: x = - 3.
Где F - фокус, a - большая (действительная) полуось, b - малая (мнимая) полуось, D - директриса кривой.
Решение:
а) Каноническое уравнение эллипса имеет вид
По условию задачи большая полуось 
. Для эллипса выполняется равенство 
. Подставив в него значения 
и 
, найдем 
. Тогда искомое уравнение эллипса
б) Каноническое уравнение гиперболы имеет вид
По условию мнимая полуось 
. Для гиперболы справедливо равенство 
. Поэтому 
. Записываем искомое уравнение гиперболы:
в) Каноническое уравнение параболы в данном случае должно иметь вид
,
а уравнение ее директрисы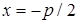 
. Но по условию задачи уравнение директрисы 
. Поэтому 
и искомое каноническое уравнение параболы имеет вид
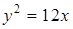
Задание 4. Записать уравнение окружности, проходящей через фокусы эллипса 
и имеющей центр в его верхней вершине.
Решение:
Для данного эллипса 
верхняя вершина 
, 
, 
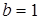. Поэтому
и фокусы находятся в точках 
. Радиус R искомой окружности вычисляем по формуле расстояния между двумя точками:
В соответствии с каноническим уравнением окружности
записываем искомое уравнение окружности:
или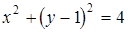 
.
Задание 5. Построить кардиоиду, заданную уравнением в полярной системе координат
Решение: Составим таблицу, в которой приведены значения полярного угла 
и соответствующие им значения полярного радиуса 
:
| j i | 0 | p/6 | p/4 | p/3 | p/2 | 2p/3 | 3p/4 | 5p/6 | p | 7p/6 |
| r i | 4 | 2 | 1,2 | 0,6 | 0 | 0,6 | 1,2 | 2 | 4 | 6 |
| j i | 5p/4 | 4p/3 | 3p/2 | 5p/3 | 7p/4 | 11p/6 |
| r i | 6,8 | 7,4 | 8 | 7,4 | 6,8 | 6 |
Построив найденные точки 
в полярной системе координат (отложив угол 
от полярной оси и вдоль полученной прямой расстояние r) и соединив их плавной линией, получим достаточно точное представление о кардиоиде (рис. 2).
 |
Рис. 2
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 3 "ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ"
Перед выполнением контрольной работы № 3 необходимо изучить следующие разделы и понятия высшей математики: числовые множества, определение и способы задания функции, пределы числовых последовательностей и функций, виды основных неопределенностей и способы их раскрытия, замечательные пределы, сравнение бесконечно малых функций, непрерывность функций, точки разрыва и их классификация.
При вычислении пределов функций или числовых последовательностей необходимо вначале определить тип неопределенности (если таковая имеется при вычислении предела), а затем в соответствии с типом неопределенности выбрать метод ее раскрытия. Выполнение контрольной работы № 3 не предусматривает использование правила Лопиталя.
Литература: /1/ гл. 5 § 5.1-5.5; гл. 6 § 6.1-6.7;
/2/ гл. 3 §2; гл. 4 § 1, 3-11;
/3/ гл. 6 § 1-6.
ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА
Задание 1. Найти предел функции 
Решение: Имеем неопределенность вида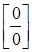 
. Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель 
, который при 
не равен нулю. В результате неопределенность будет раскрыта.
Задание 2. Найти предел функции 
Решение: Имеем неопределенность вида 
. Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
.
или
.
Задание 3. Найти предел функции 
Решение: Имеем неопределенность вида . Раскрываем ее аналогично тому как это сделано в примере 2.
Задание 4. Найти предел функции 
Решение: Имеем неопределенность вида 
. Раскрываем ее аналогично тому как это сделано в примере 2.
Задание 5. Найти предел функции 
Решение: Имеем неопределенность вида 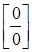. Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение стоящее в знаменателе на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель 
, который при 
не равен нулю. В результате неопределенность будет раскрыта.
Задание 6. Найти предел функции 
Решение: Имеем неопределенность вида 
. Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом 
.
Задание 7. Найти предел функции 
Решение: В данном примере при выяснении вида неопределенности видим, что таковой не имеется.
Имеем 
, тогда
Задание 8. Найти предел, используя эквивалентные бесконечно малые функции
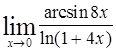
Решение: Имеем неопределенность вида 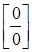. Для ее раскрытия воспользуемся теоремой о замене бесконечно малых функций эквивалентными им бесконечно малыми. Так как 
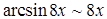и 
, то
Задание 9. Исследовать данную функцию на непрерывность и построить ее график
Решение:
Функция 
является неэлементарной, так как на разных интервалах представлена различными аналитическими выражениями. Эта функция определена на интервалах 
, где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках 
и 
.
Для точки имеем:
, 
, 
.
Так как 
, то функция 
в точке 
имеет разрыв первого рода.
Для точки 
находим:
,
,
.
Так как 
, то функция в точке 
имеет разрыв первого рода.
График данной функции изображен на рис. 3.
 |
Рис. 3.
Задание 10. Исследовать данную функцию на непрерывность в указанных точках
Решение:
Для точки 
имеем:
,
,
т.е. в точке 
функция 
имеет разрыв второго рода (терпит бесконечный разрыв).
Для точки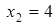 
имеем:
,
,
Следовательно, в точке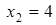 
функция непрерывна.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 4 "ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ"
Перед выполнением контрольной работы № 4 необходимо изучить следующие разделы и понятия высшей математики производная, ее геометрический и физический смысл, правила и формулы дифференцирования; логарифмическое дифференцирование; производные высших порядков; дифференциалы первого и высших порядков и их приложения; теоремы о среднем и правило Лопиталя; исследования поведения функции и их графиков; схема полного исследования функции и построение ее графика.
Литература: /1/ гл. 7 § 7.1-7.7; гл. 8 § 8.1-8.9;
/2/ гл. 5 § 1, 4-6, 8, 9, 12, 13, 15;
/3/ гл. 7 § 1, 2.
ПРИМЕР РЕШЕНИЯ ТИПОВОГО ВАРИАНТА
Задание 1. Найти производную функции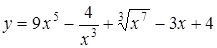 
Решение:
Задание 2. Найти производную функции 
Решение:
Задание 3. Найти производную функции 
Решение:
Задание 4. Найти производную функции 
Решение:
Задание 5. Найти производную функции 
Решение:
Задание 6. Найти производную функции 
Решение:
Задание 7. Используя метод логарифмического дифференцирования, вычислить производную функции
Решение: Применим метод логарифмического дифференцирования. Для этого предварительно прологарифмируем обе части данного выражения и используя свойства логарифма преобразуем правую часть.
.
Продифференцируем обе части равенства, учитывая, что y сложная функция
,
.
Выражая производную искомой функция, получим
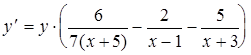
Учитывая, что 
, окончательно получим
.
Задание 8. Провести полное исследование функции и построить ее график
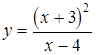
Решение:
Проведем полное исследование функции, используя следующую схему:
1. найти область определения функции;
2. исследовать на четность и нечетность функцию;
3. найти точки разрыва функции;
4. найти асимптоты (вертикальные, наклонные и горизонтальные) графика функции;
5. найти точки пересечения графика функции с координатными осями;
6. исследовать функцию на монотонность (указав интервалы возрастания и убывания) и экстремум;
7. определить интервалы выпуклости и вогнутости графика функции, точки перегиба;
8. при необходимости вычислить значения функции в дополнительных точках;
9. построить схематично график функции, используя результаты полученные в пунктах 1-8.
1. Областью определения функции является множество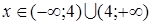 
.
2. Так как 
и 
, то функция не является ни четной, ни нечетной.
3. Функция претерпевает разрыв в точке 
.
4. Найдем асимптоты графиков функции:
а). Прямая 
является вертикальной асимптотой, т.к.
, 
б). Находим наклонные и горизонтальные асимптоты (горизонтальные асимптоты являются частным случаем наклонных асимптот) 
,
где 
;
Таким образом, прямая 
является единственной наклонной асимптотой и на 
, и на 
.
5. Найдем точки пересечения графика функции с осями координат.
а) С осью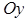 
: 
, 
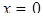, т.е. точка пересечения с осью -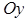 
.
б) С осью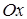 
: 
, 
, т.е. точка пересечения с осью 
- 
.
6. Исследуем функцию на возрастание, убывание и экстремум. Для этого найдем производную функции.
Из 
получаем 
, откуда 
, 
.
+ _ +
x
-3 11
Так как на интервалах 
и 
производная положительна, т.е. 
, то график функции на указанных интервалах возрастает. Так как на интервале 
производная отрицательна, т.е.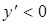 
, то на указанном интервале график функции убывает.
Так как при переходе через точки 
, производная функции меняет знаки и эти точки входят в область определения функции, то , 
- точки локального экстремума. Причем 
точка локального минимума: 
(так как при переходе через нее производная меняет знак с "+" на "-"); - точка локального максимума: 
(так как при переходе через нее производная меняет знак с "-" на "+").
7. Исследуем график функции на выпуклость, вогнутость и определим точки перегиба. Для этого найдем вторую производную функции.
Очевидно, что в интервале 
вторая производная меньше нуля, т.е. 
, и в этом интервале график функции является выпуклым вверх. В интервале 
вторая производная больше нуля, т.е. 
, и в этом интервале график функции является выпуклым вниз (вогнутым).
Несмотря на то, что при переходе через точку 
вторая производная меняет знак, она не является точкой перегиба, так как не входит в область определения функции, т.е. функция в ней не определена. Таким образом, точек перегиба у графика функции нет.
Из получаем 
, откуда 
, 
.
+ _ +
x
-3 11
Так как на интервалах и 
производная положительна, т.е. , то график функции на указанных интервалах возрастает. Так как на интервале 
производная отрицательна, т.е. 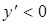, то на указанном интервале график функции убывает.
Так как при переходе через точки , производная функции меняет знаки и эти точки входят в область определения функции, то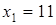 
, 
- точки локального экстремума. Причем точка локального минимума: (так как при переходе через нее производная меняет знак с "+" на "-"); 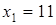- точка локального максимума: (так как при переходе через нее производная меняет знак с "-" на "+").
8. График функции изображен на рис. 4.
Рис. 4.
ЛИТЕРАТУРА
ОСНОВНАЯ ЛИТЕРАТУРА
1. Высшая математика для экономистов: Учебное пособие для вузов/Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Под ред. проф. Кремера Н.Ш. –М.: Банки и биржи, ЮНИТИ, 1997. – 439 с.
2. Шипачев В.С. Высшая математика. Учеб. Для вузов. - 3-е изд., стер. - М.: Высш.школа. 1996. - 479 с.
3. Данко П. Е., Попов А. Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.1. - М.: Высш. шк., 1986. – 304 с.
4. Бронштейн И.Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. - М.: Наука, 1986. – 544 с.
<
