Предварительные леммы

Лемма Если группа 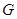 является произведением двух подгрупп  и 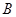 взаимно простых порядков и  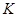--- субинвариантная в  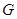подгруппа, то .

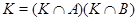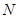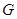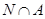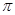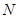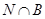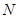Доказательство. Если  --- инвариантная в  подгруппа, то  --- -холловская в  подгруппа, где , а  --- -холловская в  подгруппа(9). Поэтому 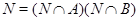. Если теперь  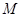--- инвариантная в  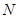подгруппа, то опять

и т. д.

Лемма Если группа 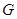 является произведением примарной подгруппы нечетного порядка и 2-разложимой подгруппы, то  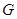разрешима.

Доказательство. Пусть 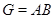,  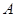--- -группа,  --- нечетное простое число, 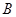 --- 2-разложимая группа. В  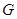существует силовская -подгруппа 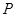 такая, что 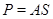, где 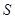 --- некоторая силовская -подгруппа из (7). Так как 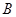 разрешима, то 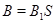, где 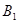 --- -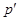холловская подгруппа из . Но теперь 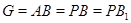. По лемме Бернсайда (5)группа  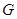непроста. Инвариантная подгруппа  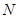в 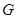 по лемме факторизуема, т. е. 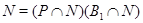, поэтому  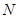разрешима по индукции. Фактор-группа  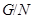также разрешима по индукции. Поэтому разрешима и .

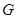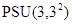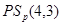Лемма Группы  и  не содержат бипримарные холловские подгруппы.

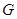Доказательство. Пусть . Тогда порядок  равен 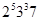 и силовская 7-подгруппа в  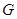самоцентрализуема. Так как порядок  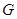больше порядка 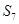, то 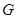 не содержит подгруппы порядка .

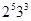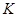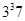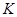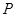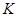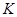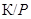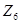Предположим, что существует подгруппа  порядка . По теореме Силова о числе силовских подгрупп подгруппа  7-замкнута, т. е. подгруппа  порядка 7 из  инвариантна в . Но теперь  изоморфна подгруппе группы всех автоморфизмов , которая изоморфна . Противоречие.

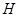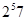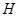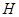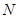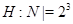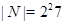Допустим, что есть подгруппа  порядка . Как и в предыдущем случае, подгруппа  не может быть 7-замкнутой. Так как индекс в  нормализатора  силовской 7-подгруппы сравним с 1 по модулю 7, то  и . Поэтому 4 должно делить порядок 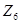, а это невозможно. Таким образом, в  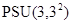нет бипримарных холловских подгрупп.

Теперь пусть 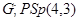. Тогда порядок  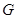равен 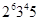, силовская 3-подгруппа  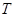из 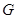 неабелева и 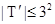. Силовская 2-подгруппа  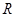также неабелева и  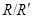имеет экспоненту 2. Нормализатор силовской 5-подгруппы  в 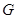 имеет порядок 20, а централизатор  в 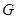 совпадает с  [??].

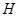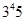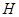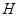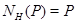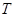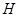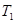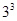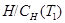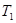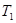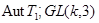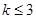Предположим, что существует подгруппа  порядка . Тогда  3-замкнута, а так как  ненильпотентна, то . Подгруппа  неабелева, поэтому минимальная инвариантная в  подгруппа  имеет порядок не более чем . Теперь  изоморфна подгруппе из группы всех авторморфизмов . Но  --- элементарная абелева, поэтому , где , и 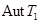 имеет порядок, не делящийся на 5. Таким образом, 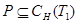, но тогда 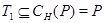. Противоречие.

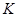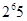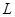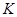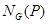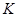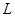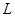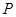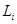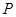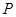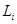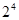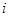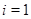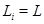Допустим, что существует подгруппа  порядка . Пусть  --- минимальная инвариантная в  подгруппа. Так как  имеет порядок 20, то  неинвариантна в  и  есть 2-группа. По теореме Машке [??] подгруппа  есть прямое произведение неприводимых -групп . Подгруппа  самоцентрализуема, поэтому  не централизуют  и по [??] порядок  равен  для всех . Следовательно,  и . Фактор-группа  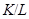имеет порядок 20, поэтому она 5-замкнута и  инвариантна в . 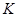Теперь 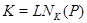. Пересечение  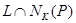инвариантно в 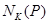, поэтому 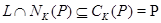. Таким образом, 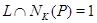, и  изоморфна циклической группе порядка 4 из 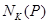. Это противоречит тому, что  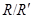имеет экспоненту 2.

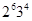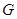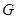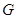Если G содержит подгруппу порядка , то индекс этой подгруппы в  будет равен 5. Поэтому  изоморфна подгруппе симметрической группы  степени 5. Но порядок  больше порядка 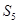. Противоречие.

Лемма Группа 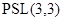 содержит подгруппу порядка  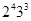и не содержит бипримарные холловские подгруппы других порядков.

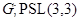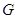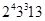Доказательство. Пусть . Тогда порядок  равен  и 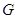 --- дважды транзитивная группа степени 13. Поэтому стабилизатор  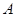одной точки будет холловской подгруппой порядка 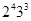. Силовская 3-подгруппа в  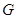неабелева. Нормализатор силовской 13-подгруппы имеет порядок 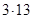, а централизатор --- 13 [??].

Пусть  --- подгруппа порядка 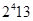. По теореме Силова  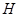--- 13-замкнута. Поэтому центр  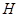неединичен. Противоречие.

Допустим, что есть подгруппа 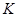 порядка . Так как 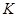 не 13-замкнута, то минимальная инвариантная в  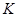подгруппа  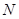есть 3-группа. Подгруппа  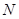абелева, поэтому 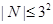. Теперь силовская 13-подгруппа централизует 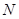. Значит, центр  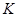отличен от 1. Противоречие.