БИПРИМАРНЫЕ ГРУППЫ
Исполнитель:
студентка группы H.01.01.01 М-33
Стародубова Н.С.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии
Монахов В. С.
Гомель 2003
Содержание
Введение
1.Основные обозначения
2. Разрешимость факторизуемой группы с разложимыми факторами
3. О произведении 2-разложимой группы и группы Шмидта
4. Произведение бипримарной и 2-разложимой групп
5. Произведение бипримарной и примарной групп
6. Доказательство теоремы (3)
Заключение
Список литературы
Введение
В данной курсовой работе приводятся свойства конечных групп, являющихся произведением двух групп, а именно являющихся произведением двух групп, одна из которых группа Шмидта, а вторая 2-разложимая, произведением бипримарной и 2-разложимой групп.
В третьем пункте данной курсовой работы доказываются следующие теоремы:
Теорема. Пусть 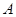 и
и 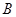 --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть  . Если подгруппы
. Если подгруппы 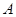 и
и 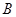
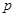 -разложимы для каждого
-разложимы для каждого 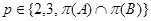 , то
, то  разрешима.
разрешима.
Теорема. Пусть 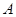 и
и 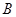 --- подгруппы конечной группы
--- подгруппы конечной группы  и пусть
и пусть  . Предположим, что
. Предположим, что 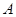 и
и 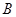 ---
--- 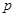 -замкнуты для каждого
-замкнуты для каждого  . Если
. Если 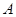 и
и 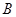
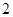 -разложимы и
-разложимы и 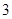 -разложимы, то
-разложимы, то  разрешима.
разрешима.
В четвертом пункте доказазываются приведенные ниже теоремы.
Теорема. Пусть 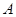 есть группа Шмидта,
есть группа Шмидта, 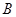 --- 2-разложимая группа, порядки
--- 2-разложимая группа, порядки 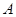 и
и 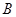 взаимно просты. Если
взаимно просты. Если 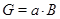 и
и  --- конечная неразрешимая группа, то
--- конечная неразрешимая группа, то 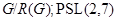 ,
,  ,
,  и
и 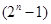 --- простое число
--- простое число 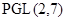 или
или 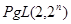 для некоторого простого
для некоторого простого 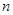 .
.
Теорема. Пусть 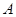 --- группа Шмидта;
--- группа Шмидта; 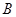 ---
--- 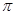 -разложимая группа, где
-разложимая группа, где  . Если
. Если 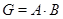 и
и  --- простая группа, то
--- простая группа, то 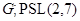 ,
,  или
или  и
и 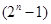 --- простое число.
--- простое число.
В пятом пункте доказываются следующие теоремы:
Теорема. Пусть конечная группа  является произведением своих подгрупп
является произведением своих подгрупп 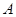 и
и 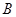 взаимно простых порядков, и пусть
взаимно простых порядков, и пусть 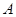 --- бипримарная группа, а
--- бипримарная группа, а 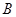 --- 2-разложимая группа четного порядка. Предположим, что в
--- 2-разложимая группа четного порядка. Предположим, что в 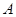 есть неединичная циклическая силовская подгруппа
есть неединичная циклическая силовская подгруппа  . Тогда, если
. Тогда, если  неразрешима, то
неразрешима, то 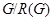 изоморфна
изоморфна 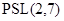 или
или 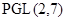 .
.
Теорема. Пусть неразрешимая группа  является произведением бипримарной подгруппы
является произведением бипримарной подгруппы 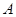 и примарной подгруппы
и примарной подгруппы 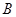 . Тогда, если среди силовских подгрупп группы
. Тогда, если среди силовских подгрупп группы  есть циклическая, то
есть циклическая, то 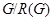 изоморфна одной из следующих групп:
изоморфна одной из следующих групп:
1) 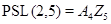 ;
;
2) 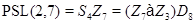 ;
;
3)  ;
;
4) 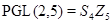 ;
;
5)  ;
;
6) 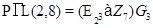 , где
, где  --- силовская 3-подгруппа;
--- силовская 3-подгруппа;
7)  , порядок
, порядок 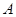 равен
равен 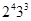 , а
, а 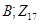 .
.
Основные обозначения

| группа |
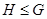
| 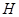 является подгруппой группы является подгруппой группы 
|
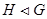
| 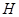 является нормальной подгруппой группы является нормальной подгруппой группы 
|
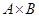
| прямое произведение подгрупп 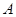 и и 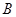
|
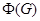
| подгруппа Фраттини группы 
|
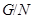
| фактор-группа группы  по по 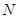
|

| множество всех простых делителей натурального числа 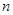
|
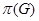
| множество всех простых делителей порядка группы 
|
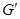
| коммутант группы 
|
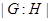
| индекс подгруппы 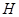 в группе в группе 
|
Разрешимость факторизуемой группы с разложимыми факторами
Конечная группа называется 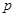 -разложимой для простого числа
-разложимой для простого числа 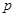 , если силовская
, если силовская 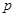 -подгруппа выделяется в ней прямым множителем. Нильпотентная группа
-подгруппа выделяется в ней прямым множителем. Нильпотентная группа 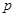 -разложима для каждого
-разложима для каждого 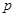 . Через
. Через 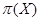 обозначается множество всех простых делителей порядка группы
обозначается множество всех простых делителей порядка группы 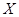 .
.
Теорема Пусть 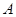 и
и 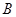 --- подгруппы конечной группы
--- подгруппы конечной группы 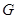 и пусть
и пусть  . Если подгруппы
. Если подгруппы 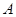 и
и 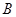
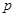 -разложимы для каждого
-разложимы для каждого 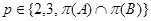 , то
, то 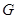 разрешима.
разрешима.
Теорема (1) обобщает известную теорему Виландта-Кегеля о разрешимости конечной группы, являющейся произведением нильпотентных подгрупп [??].
Для доказательства теоремы (2) нам потребуется следующая лемма(3), которая несколько уточняет лемму Кегеля(4). Напомним, что 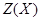 --- центр
--- центр 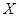 , а если
, а если 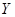 --- подгруппа группы
--- подгруппа группы 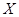 , то
, то 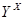 --- наименьшая нормальная в
--- наименьшая нормальная в 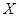 подгруппа, содержащая
подгруппа, содержащая 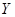 . Группа
. Группа 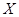 называется
называется 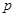 -замкнутой, если в ней силовская
-замкнутой, если в ней силовская 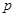 -подгруппа
-подгруппа 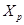 нормальна.
нормальна.
Лемма Пусть 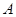 и
и 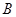 --- подгруппы конечной группы
--- подгруппы конечной группы  , обладающие следующими свойствами:
, обладающие следующими свойствами:
1) 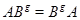 для всех
для всех 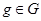 ;
;
2) 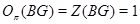 , где
, где 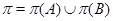 .
.
Тогда 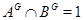 .
.
Доказательство. Воспользуемся методом доказательства леммы Кегеля. Пусть 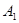 --- наибольшая
--- наибольшая  -подгруппа, содержащая
-подгруппа, содержащая  и перестановочная с каждой подгруппой, сопряженной с
и перестановочная с каждой подгруппой, сопряженной с 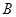 . Предположим, что
. Предположим, что 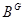 не содержится в
не содержится в 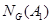 . Это означает, что существуют элементы
. Это означает, что существуют элементы 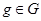 и
и 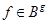 такие, что
такие, что  не принадлежит
не принадлежит 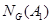 . Поэтому
. Поэтому 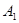 --- собственная подгруппа в
--- собственная подгруппа в 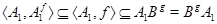 и
и  есть
есть 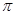 -группа. Кроме того,
-группа. Кроме того,  перестановочна с каждой сопряженной с
перестановочна с каждой сопряженной с 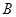 подгруппой, так как этим свойством обладает
подгруппой, так как этим свойством обладает 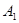 . Теперь
. Теперь 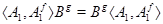 для всех
для всех 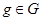 , что противоречит выбору
, что противоречит выбору 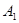 .
.
Итак, 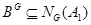 . Значит,
. Значит, 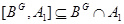 и
и 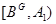 --- нормальная в
--- нормальная в 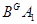
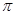 -подгруппа. Из условия 2) следует, что
-подгруппа. Из условия 2) следует, что 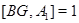 и
и  . Так как
. Так как 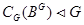 и
и 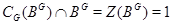 , то
, то 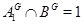 . Поэтому
. Поэтому 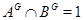 .
.
Лемма Пусть конечная группа 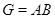 с
с 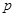 -замкнутыми подгруппами
-замкнутыми подгруппами 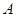 и
и 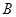 . Если
. Если 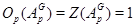 , то
, то 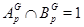 .
.
Доказательство. Так как 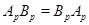 , то
, то 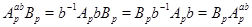 для всех
для всех 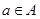 ,
, 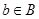 . Первое условие леммы (5) выполнено. Так как выполняется и второе, то
. Первое условие леммы (5) выполнено. Так как выполняется и второе, то  .
.
Секцией группы 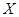 называется фактор-группа некоторой подгруппы из
называется фактор-группа некоторой подгруппы из 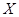 . Если
. Если 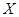 не содержит секций, изоморфных симметрической группе
не содержит секций, изоморфных симметрической группе 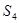 четырех символов, то
четырех символов, то 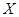 называется
называется 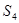 -свободной.
-свободной.
Лемма Если конечная группа 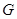 не является
не является 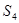 -свободной, то существуют
-свободной, то существуют 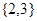 -подгруппы
-подгруппы 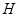 и
и 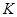 такие, что
такие, что 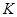 нормальна в
нормальна в 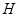 и
и 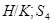 .
.
Доказательство. По условию в группе 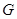 существует секция
существует секция 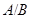 , изоморфная
, изоморфная 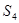 . Пусть
. Пусть  --- нормальная в
--- нормальная в 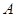 подгруппа индекса
подгруппа индекса 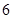 , содержащая подгруппу
, содержащая подгруппу 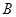 с индексом
с индексом 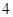 . По лемме Фраттини
. По лемме Фраттини 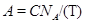 , где
, где 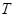 --- силовская
--- силовская 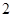 -подгруппа из
-подгруппа из 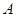 , Так как
, Так как 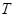 имеет индекс
имеет индекс  в силовской
в силовской  -подгруппе из
-подгруппе из 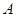 , то
, то  разрешима и содержит
разрешима и содержит 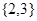 -холловскую подгруппу
-холловскую подгруппу 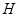 . Кроме того,
. Кроме того, 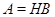 и
и 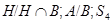 .
.
Лемма Конечная группа, содержащая нильпотентную 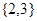 -холловскую подгруппу,
-холловскую подгруппу, 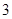 -разрешима.
-разрешима.
Доказательство. Достаточно показать непростоту группы 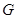 в случае, когда
в случае, когда 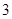 делит
делит 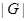 . Предположим, что
. Предположим, что 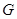 простая и
простая и 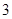 делит
делит 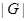 . В
. В 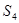 -свободных группах нет нильпотентных
-свободных группах нет нильпотентных 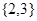 -холловских подгрупп [??], отличных от
-холловских подгрупп [??], отличных от 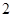 -силовской. Если
-силовской. Если 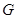 не
не 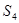 -свободна, то по лемме (??) существует ненильпотентная
-свободна, то по лемме (??) существует ненильпотентная 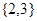 -подгруппа. Это противоречит теореме Виландта [??]. Лемма доказана.
-подгруппа. Это противоречит теореме Виландта [??]. Лемма доказана.
Через 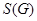 обозначим произведение всех разрешимых нормальных в
обозначим произведение всех разрешимых нормальных в 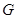 подгрупп.
подгрупп.
Лемма Пусть конечная группа 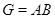 и пусть
и пусть 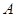 разрешима, а
разрешима, а 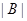 взаимно прост с
взаимно прост с  . Если в
. Если в 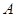 существует нилъпотентная
существует нилъпотентная 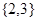 -холловская подгруппа, то
-холловская подгруппа, то 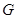 разрешима.
разрешима.
Доказательство. Если 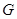 ---
--- 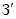 -группа, то
-группа, то 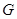 разрешима по лемме Сыскина(2). Пусть
разрешима по лемме Сыскина(2). Пусть 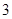 делит
делит 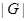 и
и 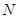 --- минимальная нормальная в
--- минимальная нормальная в 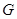 подгруппа. Если
подгруппа. Если 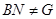 , то
, то  и
и 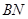 разрешима по индукции, поэтому разрешима и
разрешима по индукции, поэтому разрешима и 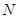 . Пусть
. Пусть 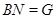 . Тогда
. Тогда 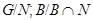 и
и  имеет порядок взаимно простой с
имеет порядок взаимно простой с  . Значит нильпотентная
. Значит нильпотентная 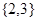 -холловская подгруппа из
-холловская подгруппа из 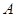 содержится в
содержится в  и
и 
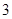 -разрешима по лемме(2). Из минимальности
-разрешима по лемме(2). Из минимальности  следует, что
следует, что  разрешима. Итак, в любом случае
разрешима. Итак, в любом случае 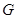 содержит разрешимую нормальную подгруппу
содержит разрешимую нормальную подгруппу  . Фактор-группа
. Фактор-группа  удовлетворяет условиям леммы и по индукции разрешима. Поэтому разрешима и
удовлетворяет условиям леммы и по индукции разрешима. Поэтому разрешима и 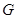 . Лемма доказана.
. Лемма доказана.
Теорема (??) вытекает из следующей более общей теоремы
Теорема Пусть 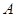 и
и 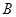 --- подгруппы конечной группы
--- подгруппы конечной группы 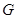 и пусть
и пусть  . Предположим, что
. Предположим, что 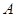 и
и 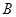 ---
--- 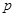 -замкнуты для каждого
-замкнуты для каждого  . Если
. Если 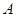 и
и 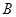
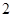 -разложимы и
-разложимы и 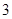 -разложимы, то
-разложимы, то 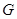 разрешима.
разрешима.
Доказательство индукцией по порядку 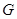 . Пусть
. Пусть 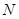 --- минимальная нормальная в
--- минимальная нормальная в 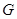 подгруппа. Фактор-группа
подгруппа. Фактор-группа  , а подгруппы
, а подгруппы 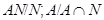 и
и 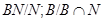 будут
будут  - и
- и 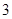 -разложимыми и
-разложимыми и 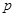 -замкнутыми для каждого
-замкнутыми для каждого  . По индукции
. По индукции  разрешима, а
разрешима, а 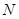 неразрешима. Поэтому
неразрешима. Поэтому 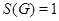 и
и 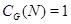 . Следовательно, в
. Следовательно, в 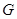 единственная минимальная нормальная подгруппа.
единственная минимальная нормальная подгруппа.
Пусть 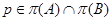 и пусть
и пусть 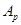 и
и 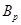 --- силовские
--- силовские 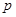 -подгруппы из
-подгруппы из 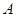 и
и 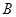 соответственно. Так как
соответственно. Так как 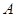 и
и 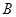 р-замкнуты и
р-замкнуты и 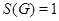 , то
, то 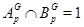 по лемме (??). Но
по лемме (??). Но  содержит точно одну минимальную нормальную подгруппу. Поэтому либо
содержит точно одну минимальную нормальную подгруппу. Поэтому либо 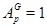 , либо
, либо  . Итак для каждого
. Итак для каждого 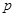 , либо
, либо 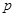 не делит
не делит 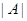 , либо
, либо 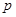 не делит
не делит 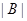 . Следовательно, порядки
. Следовательно, порядки 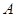 и
и 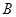 взаимно просты. Но теперь
взаимно просты. Но теперь 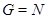 --- простая группа.
--- простая группа.
Так как группа Судзуки 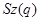 нефакторизуема(4), то по теореме Глаубермана (4)порядок
нефакторизуема(4), то по теореме Глаубермана (4)порядок  делится на
делится на 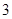 , а по теореме Фомина (2) порядок одного из факторов, пусть порядок
, а по теореме Фомина (2) порядок одного из факторов, пусть порядок 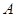 , делится на
, делится на  . Теперь в
. Теперь в  существует нильпотентная
существует нильпотентная 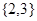 -холловская подгруппа. По лемме (3)группа
-холловская подгруппа. По лемме (3)группа  разрешима. Теорема доказана.
разрешима. Теорема доказана.
 2020-01-15
2020-01-15 104
104







