2020-01-15
94
В (1) описаны конечные неразрешимые группы, являющиеся произведением двух подгрупп взаимно простых порядков, одна из которых есть группа Шмидта, а вторая --- 2-разложимая группа (см. также(2)). Все свойства группы Шмидта хорошо известны, в частности, она бипримарна, т. е. ее порядок делится в точности на два различных простых числа, и в ней содержится неединичная циклическая силовская подгруппа.
Развивая указанный результат работы(6), мы доказываем в настоящей заметке следующую теорему.
Теорема Пусть конечная группа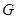 
является произведением своих подгрупп 
и 
взаимно простых порядков, и пусть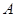 
--- бипримарная группа, а 
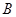--- 2-разложимая группа четного порядка. Предположим, что в есть неединичная циклическая силовская подгруппа 
. Тогда, если 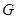неразрешима, то 
изоморфна 
или 
.
обозначает произведение всех разрешимых инвариантных в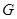 
подгрупп.
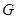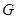Следствие Пусть группа обладает факторизацией, указанной в теореме(3). Тогда, если порядок не равен 3 или 1, то разрешима.
Доказательство теоремы 1 начинается с изучения частного случая, когда подгруппа примарная. Описанию этого случая, причем без предположения четности порядка подгруппы , посвящена
Теорема Пусть неразрешимая группа 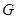является произведением бипримарной подгруппы 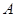и примарной подгруппы . Тогда, если среди силовских подгрупп группы 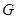есть циклическая, то 
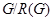изоморфна одной из следующих групп:
1) 
;
2) 
;
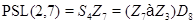3) 
;
4) 
;
5) 
;
6) 
, где 
--- силовская 3-подгруппа;
7) 
, порядок 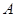равен 
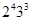, а 
.
Так как бипримарные группы разрешимы, то группа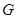 
из теоремы (7) имеет порядок, делящийся в точности на три различных простых числа. Такие простые группы к настоящему времени известны лишь в случае, когда они содержат циклическую силовскую подгруппу. Этим и вызвано требование цикличности силовской подгруппы в условии теоремы(8), а следовательно, и в условии теоремы(8).
Если будут известны все простые группы порядка 
, где 
, 
и 
--- различные простые числа, то методы доказательства теоремы (5) позволят описать неразрешимые группы с указанной в теореме (5) факторизацией без предположения цикличности подгруппы .
Используются следующие обозначения: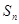 
и 
--- симметрическая и знакопеременная группы степени 
, 
, 
и 
--- циклическая, элементарная абелева и соответственно диэдральная группы порядка . Полупрямое произведение групп 
и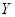 
с инвариантной подгруппой обозначается через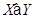 
. Примарной называется группа, порядок которой есть степень простого числа.
