Допустим, что теорема неверна и группа 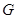 --- контрпример минимального порядка. Пусть
--- контрпример минимального порядка. Пусть 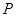 --- циклическая силовская
--- циклическая силовская 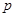 -подгруппа в
-подгруппа в 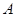 , а
, а 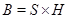 , где
, где 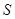 --- силовская 2-подгруппа в
--- силовская 2-подгруппа в 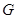 ,
, 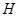 --- ее инвариантное дополнение в
--- ее инвариантное дополнение в 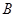 . В силу леммы (??) условие теоремы выполняется для
. В силу леммы (??) условие теоремы выполняется для 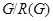 , поэтому мы можем считать, что
, поэтому мы можем считать, что 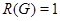 .
.
Пусть 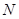 --- минимальная инвариантная в
--- минимальная инвариантная в 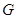 подгруппа. Тогда
подгруппа. Тогда 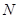 неразрешима,
неразрешима, 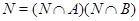 и по лемме (??) порядок
и по лемме (??) порядок 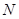 делится на
делится на 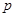 . Силовская
. Силовская 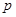 -подгруппа
-подгруппа 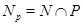 циклическая, поэтому
циклическая, поэтому 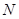 --- простая группа. Теперь, если
--- простая группа. Теперь, если 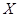 --- другая инвариантная в
--- другая инвариантная в 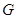 подгруппа, то силовская
подгруппа, то силовская 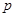 -подгруппа
-подгруппа 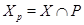 пересекается с
пересекается с 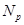 не по единице. Из минимальности
не по единице. Из минимальности 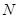 следует, что
следует, что 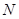 содержится в
содержится в 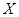 . Таким образом,
. Таким образом, 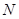 --- единственная минимальная инвариантная в
--- единственная минимальная инвариантная в 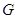 подгруппа. Так как централизатор
подгруппа. Так как централизатор 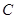 подгруппы
подгруппы 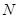 инвариантен в
инвариантен в 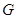 и пересекается с
и пересекается с 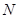 по единице, то и
по единице, то и 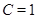 . Следовательно,
. Следовательно, 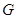 изоморфна подгруппе группы автоморфизмов группы
изоморфна подгруппе группы автоморфизмов группы 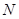 .
.
Если 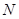 --- собственная в
--- собственная в 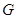 подгруппа, то по индукции
подгруппа, то по индукции 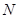 изоморфна
изоморфна 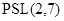 . Но тогда
. Но тогда 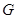 изоморфна
изоморфна 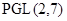 , противоречие.
, противоречие.
Таким образом, 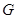 --- простая группа. В силу теоремы (??) подгруппа
--- простая группа. В силу теоремы (??) подгруппа 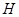 неединична.
неединична.
Введем следующие обозначения: 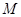 --- минимальная инвариантная в
--- минимальная инвариантная в 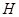 подгруппа,
подгруппа, 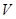 --- силовская подгруппа из
--- силовская подгруппа из 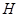 , содержащая
, содержащая 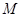 ,
, 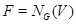 . Так как
. Так как 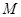 инвариантна в
инвариантна в 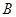 , то
, то 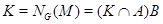 .
.
Допустим, что 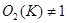 . Напомним, что
. Напомним, что 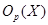 --- наибольшая инвариантная в группе
--- наибольшая инвариантная в группе 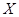
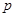 -подгруппа. Так как
-подгруппа. Так как 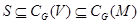 и
и 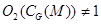 , то и
, то и 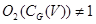 . Поэтому
. Поэтому 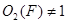 . Пусть
. Пусть 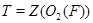 . Покажем, что
. Покажем, что 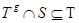 для всех
для всех 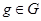 . Возьмем произвольный элемент
. Возьмем произвольный элемент 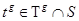 ,
, 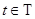 . Тогда
. Тогда 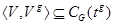 , поэтому
, поэтому 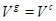 для некоторого
для некоторого 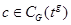 . Теперь
. Теперь 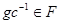 . Так как
. Так как 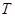 инвариантна в
инвариантна в 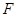 , то
, то 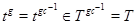 . По теореме Гольдшмидта получаем, что либо
. По теореме Гольдшмидта получаем, что либо  абелева, либо
абелева, либо  изоморфна
изоморфна 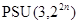 или
или 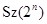 . Если
. Если 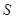 абелева, то группа
абелева, то группа 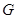 разрешима, противоречие. Так как
разрешима, противоречие. Так как 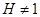 , то изоморфизм
, то изоморфизм 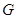 с группами
с группами 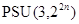 и
и 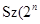 ) невозможен.
) невозможен.
Таким образом, 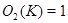 . Группа
. Группа 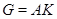 , и
, и 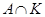 не содержит подгрупп, инвариантных в
не содержит подгрупп, инвариантных в 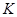 . По лемме 1 из [??] группа
. По лемме 1 из [??] группа 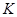 неразрешима. Значит,
неразрешима. Значит, 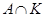 бипримарна, и
бипримарна, и 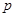 делит порядок
делит порядок 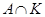 . По индукции
. По индукции 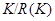 изоморфна
изоморфна 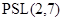 или
или 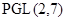 .
.
Допустим, что 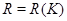 имеет четный порядок. Подгруппа
имеет четный порядок. Подгруппа 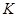 факторизуема, a
факторизуема, a 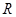 инвариантна в
инвариантна в 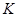 , значит, и
, значит, и 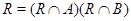 . Если
. Если 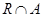 содержит неединичную подгруппу, инвариантную в
содержит неединичную подгруппу, инвариантную в 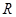 , то и
, то и 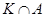 содержит подгруппу, инвариантную в
содержит подгруппу, инвариантную в 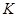 , противоречие. По лемме 1 из [??] подгруппа
, противоречие. По лемме 1 из [??] подгруппа 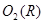 неединична, противоречие. Следовательно, порядок
неединична, противоречие. Следовательно, порядок 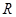 нечетен.
нечетен.
Теперь силовская 2-подгруппа 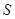 из
из 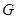 изоморфна силовской 2-подгруппе из группы
изоморфна силовской 2-подгруппе из группы 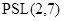 или
или 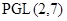 , т. е.
, т. е. 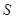 --- диэдральная группа порядка 8 или 16. Поэтому и изоморфна
--- диэдральная группа порядка 8 или 16. Поэтому и изоморфна 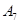 или
или 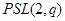 ,
, 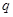 нечетное. Но этот изоморфизм ввиду
нечетное. Но этот изоморфизм ввиду 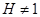 невозможен. Теорема доказана.
невозможен. Теорема доказана.
Доказательство следствия теоремы. Пусть утверждение неверно и группа 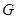 --- контрпример минимального порядка. Фактор-группа
--- контрпример минимального порядка. Фактор-группа 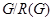 неразрешима и по теореме она изоморфна
неразрешима и по теореме она изоморфна 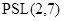 или
или 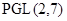 . Поэтому порядок
. Поэтому порядок 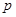 -группы
-группы 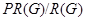 равен 3 или 7. Значит,
равен 3 или 7. Значит, 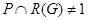 . Теперь, повторяя дословно второй и третий абзацы доказательства следствия теоремы, мы приходим к противоречию.
. Теперь, повторяя дословно второй и третий абзацы доказательства следствия теоремы, мы приходим к противоречию.
Заключение
Итак, в данной курсовой работе приводятся свойства конечных групп, являющихся произведением двух групп, одна из которых группа Шмидта, а вторая 2-разложимая, произведением бипримарной и 2-разложимой групп. Доказываются следующие теоремы:
Теорема. Пусть 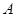 и
и 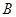 --- подгруппы конечной группы
--- подгруппы конечной группы 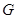 и пусть
и пусть 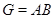 . Если подгруппы
. Если подгруппы 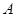 и
и 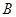
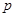 -разложимы для каждого
-разложимы для каждого 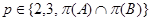 , то
, то 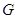 разрешима.
разрешима.
Теорема. Пусть 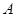 и
и 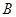 --- подгруппы конечной группы
--- подгруппы конечной группы 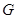 и пусть
и пусть 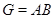 . Предположим, что
. Предположим, что 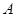 и
и 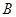 ---
--- 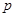 -замкнуты для каждого
-замкнуты для каждого 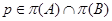 . Если
. Если 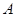 и
и 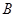
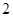 -разложимы и
-разложимы и 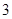 -разложимы, то
-разложимы, то 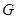 разрешима.
разрешима.
Теорема. Пусть 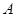 есть группа Шмидта,
есть группа Шмидта, 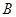 --- 2-разложимая группа, порядки
--- 2-разложимая группа, порядки 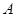 и
и 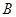 взаимно просты. Если
взаимно просты. Если 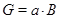 и
и 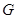 --- конечная неразрешимая группа, то
--- конечная неразрешимая группа, то 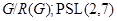 ,
, 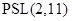 ,
, 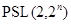 и
и 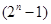 --- простое число
--- простое число 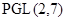 или
или 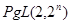 для некоторого простого
для некоторого простого 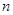 .
.
Теорема. Пусть 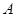 --- группа Шмидта;
--- группа Шмидта; 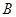 ---
--- 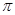 -разложимая группа, где
-разложимая группа, где 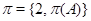 . Если
. Если 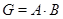 и
и 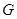 --- простая группа, то
--- простая группа, то 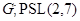 ,
, 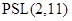 или
или 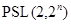 и
и 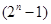 --- простое число.
--- простое число.
Теорема. Пусть конечная группа 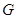 является произведением своих подгрупп
является произведением своих подгрупп 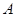 и
и 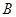 взаимно простых порядков, и пусть
взаимно простых порядков, и пусть 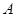 --- бипримарная группа, а
--- бипримарная группа, а 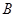 --- 2-разложимая группа четного порядка. Предположим, что в
--- 2-разложимая группа четного порядка. Предположим, что в 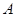 есть неединичная циклическая силовская подгруппа
есть неединичная циклическая силовская подгруппа 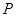 . Тогда, если
. Тогда, если 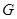 неразрешима, то
неразрешима, то 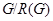 изоморфна
изоморфна 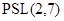 или
или 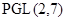 .
.
Теорема. Пусть неразрешимая группа 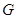 является произведением бипримарной подгруппы
является произведением бипримарной подгруппы 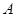 и примарной подгруппы
и примарной подгруппы 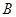 . Тогда, если среди силовских подгрупп группы
. Тогда, если среди силовских подгрупп группы 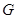 есть циклическая, то
есть циклическая, то 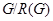 изоморфна одной из следующих групп:
изоморфна одной из следующих групп:
1) 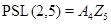 ;
;
2) 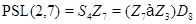 ;
;
3) 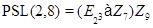 ;
;
4) 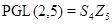 ;
;
5) 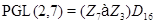 ;
;
6) 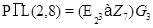 , где
, где 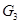 --- силовская 3-подгруппа;
--- силовская 3-подгруппа;
7) 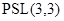 , порядок
, порядок 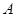 равен
равен 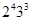 , а
, а 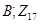 .
.
Список литературы
[1] Huppert B., Endliche Gruppen. I, Berlin--Heidelberg --- N. Y., Springer--Verlag, 1967.
[2] Glauberman G., Factorizations in local subgroups of finite groups, Reg. Con. Ser. Math., № 33, (1977), 77.
[3] Сыскин С. А., Об одном вопросе Р. Бэра, Сиб. матем. ж. 20, № 3 (1979), 679-681.
[4] Монахов В. С., Произведение сверхразрешимой и циклической или примерной групп, Сб., Конечные группы (Тр. Гомельского семинара), Минск, "Наука и техника", 1978, 50-63
[5] Фомин А. Н., Одно замечание о факторизуемых группах, Алгебра и логика, 11, № 5 (1972), 608-611.
[6] В. Huppert, Math. Zeit., 64, 138, 1956.
[7] В. А. Ведерников, Матем. зам., 3, 201, 1968.
[8] И. П. Докторов, ДАН БССР, 13, 101, 1969.
[9] П. И. Трофимов, ДАН СССР, 167, 523, 1966.
[10] В. С. Монахов, ДАН БССР, 18, № 7, 584, 1974.
[11] С. А. Чунихин, Л. А. Шеметков, сб. Итоги науки. Алгебра. Топология. Геометрия. 1969, М., 7, 1971.
[12] О. Ю. Шмидт, Матем. сб., 31, 366, 1924.
[13] L. Redei, Publ. Math. Debrecen,4, 303, 1956.
[14] В. Д. Мазуров, С. А. Сыскин, Матем. заметки, 14, 217,1973.
[15] D. Gодdsсhmidt, Not. Amer. Math. Soc., 20, № 1, 1973.
[16] Я. Г. Бeркович, ДАН СССР, 171, 770, 1966.
[17] В. С. Монахов, ДАН БССР, 15, 877, 1971.
[18] Z. Jankо, J. Algebra, 3, 147. 1966.
[19] Н. Ward, Trans. Amer. Math. Soc., 121, 62, 1966.
[20] B. Huppert, Endliche Gruppen I, Berlin, 1967.
[21] D. Wales, Algebra, 20, 124, 1972.
[22] С. А. Чyнихин, Труды семинара по теории групп, М.-Л., 1938.
[23] С. А. Чунихин, Подгруппы конечных групп, Минск, 1964.
[24] В. Huppert, N. Itо, Math. Z., 61, 94, 1954.
[25] J. Walter, Annals Math., 89, 405, 1969.
[26] N. Ito, Acta scient. math., 15, 77, 1953.
[27] В. С. Монахов, Матем. зам., 16, 285, 1974.
[28] Монахов В. С., О произведении 2-разложимой группы и группы Шмидта, Докл. АН БССР, 18, № 10 (1974), 871-874.
[29] Конечные группы, Тр. Гомельского семинара, Минск, Наука и техника, 1975.
[30] Huppert В., Endliche Gruppen, Bd. I, Berlin, Springer- Verlag, 1967.
[31] Leon J., Wales D., Simple groups of order 2aZbpc with cyclic Sylow 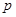 -groups, J. Algebra, 29 № 2 (1974), 246-254.
-groups, J. Algebra, 29 № 2 (1974), 246-254.
[32] Докторов И. П., Об одном классе факторизуемых групп, Докл. АН БССР, 13, № 2 (1969), 101-102.
[33] Goldschmidt D., 2-fusion in finite groups, Ann. Math., 99, № 1 (1974), 70-117.
[34] Монахов B.C., К двум теоремам Ведерникова, Докл. АН БССР, 15, № 10 (1971), 877-880.
[35] Gоrеnstein D., Walter J., The characterization of finite groups with dihedral Sylow 2-subgroups, J. Algebra, 2 (1965), 85-151, 218-270, 334-397.
 2020-01-15
2020-01-15 107
107







