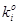2020-01-15
201
1. Найдем энтропию источника.
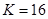- алфавит из 16 символов.
Найдем избыточность источника.
Найдем производительность источника.
.
2. Найдем минимально необходимое число разрядов кодового слова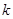 
,при условии, что производится примитивное кодирование.
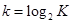
Найдем среднее количество двоичных символов, приходящееся на один символ источника. В случае примитивного кодирования:
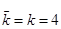
3. Построим кодовое дерево для кода Шеннона-Фано, при условии, что производится экономное кодирование. Запишем кодовые комбинации для представления всех 16 символов источника, найдем число разрядов каждой полученной комбинации.
| 
| 
|
| 
|
|
| 
| 
| ||||
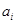
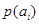
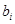
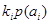
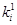
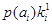
| а | 0,31 | 00 | 2 | 0,62 | 2 | 0,62 | 0 | 0 | ||||
| р | 0,2 | 01 | 2 | 0,4 | 1 | 0,2 | 1 | 0,2 | ||||
| м | 0,166 | 100 | 3 | 0,498 | 2 | 0,332 | 1 | 0,166 | ||||
| и | 0,135 | 101 | 3 | 0,405 | 1 | 0,135 | 2 | 0,27 | ||||
| в | 0,057 | 1100 | 4 | 0,228 | 2 | 0,114 | 2 | 0,114 | ||||
| л | 0,04 | 1101 | 4 | 0,16 | 1 | 0,04 | 3 | 0,12 | ||||
| д | 0,02 | 11100 | 5 | 0,1 | 2 | 0,04 | 3 | 0,06 | ||||
| е | 0,02 | 11101 | 5 | 0,1 | 1 | 0,02 | 4 | 0,08 | ||||
| н | 0,012 | 111100 | 6 | 0,072 | 2 | 0,024 | 4 | 0,048 | ||||
| б | 0,01 | 1111010 | 7 | 0,07 | 2 | 0,02 | 5 | 0,05 | ||||
| г | 0,0081 | 1111011 | 7 | 0,0567 | 1 | 0,0081 | 6 | 0,0486 | ||||
| к | 0,008 | 1111100 | 7 | 0,056 | 2 | 0,016 | 5 | 0,040 | ||||
| п | 0,006 | 1111101 | 7 | 0,042 | 1 | 0,006 | 6 | 0,036 | ||||
| о | 0,004 | 1111110 | 7 | 0,028 | 1 | 0,004 | 6 | 0,024 | ||||
| з | 0,002 | 11111110 | 8 | 0,016 | 1 | 0,002 | 7 | 0,014 | ||||
| с | 0,0019 | 11111111 | 8 | 0,0152 | 0 | 0 | 8 | 0,0152 | ||||
- число разрядов кодовой комбинации.
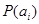-вероятность 
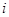-го символа.
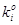и 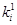- число нулей и единиц в кодовой комбинации 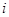-го символа.
Найдем среднее количество двоичных символов, приходящееся на один символ источника.
[бит/симв]
Избыточность на выходе кодера равна:
.
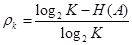Энтропия на выходе равна:
Следовательно,
Вывод: при экономном кодирования среднее число двоичных символов, приходящееся на один символ источника меньше, чем в примитивном кодировании, это доказывает эффективность экономного кодирования. Избыточность при экономном кодировании намного меньше, чем в примитивном кодировании. Примитивный равномерный код не может обеспечить эффективного согласования источника с каналом связи.
4. Рассчитаем вероятности двоичных символов на выходе кодера источника.
Рассчитаем среднюю скорость выдачи двоичных символов на выходе кодера источника.
.
