Библиографический список

 

1. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина Геометрия: учебник для 7-9 класса средней школы. - М.: Просвещение, 1990 г.

2. А.В. Погорелов Геометрия: учебник для 7-11 класса общеобразовательных учреждений. - 8-е издание - М.: Просвещение, 1998 г.

3. А.П. Киселёв, Н.А. Рыбкин Геометрия: учебник - задачник для 7-9 класса. - М. изд-во "Дрофа", 1995 г.

4. И.Ф. Шарыгин Геометрия: учебник для 7-9 класса. - 2-е издание - М. изд-во "Дрофа", 1998 г.

5. Уроки итогового повторения 7-11 классы общеобразовательной школы \ Н. Гришкова, А. Илюхина \\ "Математика" приложение к газете "1 сентября" №13, 1999 г.

6. Л. Басова Признаки равенства треугольников \\ "Математика" приложение к газете "1 сентября" №34, 2000 г.

7. И. Смирнова, В. Смирнов Самостоятельные работы по геометрии 7 класс \\ "Математика" приложение к газете "1 сентября" №33, 2001 г.

8. В. Рыжик Тесты на экзамене. Геометрия 8-11 класс \\"Математика" приложение к газете "1 сентября" №1, 2002 г.

9. Л. Птичкина Тесты повторения по геометрии 7 класс \\"Математика" приложение к газете "1 сентября" №11, 2000 г.

10. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Позняк, И.И. Юдина О конкурсном учебнике геометрии для 7-9 классов \\ Математика в школе №1, 1989 г.

11. А.В. Гладкий О некоторых определениях в учебном пособии А.В. Погорелова \\ Математика в школе №6, 1990 г.

12. В.А. Смирнов О доказательствах признаков подобия треугольников \\ Математика в школе №6, 1990 г.

13. А.Н. Колмогоров Об учебном пособии Геометрия 6-10 А.В. Погорелова \\ Математика в школе №2, 1983 г.

14. А.С. Мищенко, А.С. Понтрягин О пробном учебнике Геометрия 6-8 \\ Математика в школе №2, 1983 г.

15. А.И. Медяник Научно - методические достоинства учебного пособия по геометрии А.В. Погорелова \\ Математика в школе №2, 1983 г.

16. В.В. Пикан О практической направленности пробного учебника Геометрия 6-8 \\ Математика в школе №2, 1983 г.

Приложение

Лист 1.

.

 

Лист 2.

Докажите, что треугольники равны.

Докажите, что равны те элементы треугольников, которые отмечены знаком "?".

Лист 3,Тест

1.

 

В

ВС=10 см.

ВС=5 см.

ВС=15 см.

2.

L

K

 

3.

 

М

 

а) АС=10 м.

б) АС=20 м.

в) АС=5 м

 

 

а)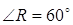

б)

в)

5. Доказать, что

 

 

а) 1) Рассмотрим Δ АВО и Δ ОСD;

2) АВ=ВО (дано);

3) DO=DC (дано);

4) AO=AB=BO (см. рисунок);

5) OD=DC=OC (см. рисунок);

6) из 2) - 5) следует, что Δ АВО и Δ ОCD равносторонние;

7) из 6)

8)  (вертикальные углы);

9) из 7) и 8)

б) 1) Рассмотрим треугольники АВО и ОСD;

2) АВ=ВО (дано);

3) DO=DC (дано);

4) из 2) и 3) Δ АВО и Δ OCD - равнобедренные;

5) из 4) следует 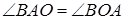 и

6)  (вертикальные углы)

7) из 5) и 6) .

Лист 4

 

Дано: Δ АВС=Δ А1В1С1; ÐА=ÐА1, ÐВ=ÐВ1. Доказать, что Δ АВС~Δ А1В1С1. Доказательство. По теореме о сумме углов треугольника… Аналогично используя равенство ÐА=ÐА1, ÐВ=ÐВ1, получаем . Итак, сходственные стороны треугольников АВС и А1В1С1 пропорциональные. Ч. т.д.

Дано: Δ KLM=Δ K1L1M1; ÐK=ÐK1; 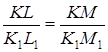. Доказать, что ΔPQR~ΔP1Q1R1. Доказательство. Учитывая первый признак достаточно доказать ÐМ=ÐМ1. Рассмотрим Δ КLM2… Отсюда следует, что ÐМ=Ð2,а т.к Ð2=ÐМ1, то ÐМ=ÐМ1. Воспользуемся первым признаком Δ КLM~Δ K1L1M1. Ч. т.д.

Дано: Δ PQR и Δ P1Q1R1; ; Доказать, что Δ PQR~Δ P1Q1R1. Доказательство. Для этого, учитывая второй признак подобия треугольников достаточно доказать, что ÐP=ÐP1. Рассмотрим треугольник PQR2… Отсюда следует ÐP=Ð1, т.к Ð1=ÐP1, то ÐP=ÐP1 Ч. т.д.

Дано: Δ АВС~Δ А1В1С1; к - коэффициент подобия; S и S1 - площади треугольников АВС и А1В1С1 соответственно. Доказать, что . Доказательство. Воспользуемся теоремой об отношении площадей треугольников имеющих по равному углу… Ч. т.д.