Признаки сходимости несобственных интегралов

 

Как было показано, несобственные интегралы сходятся не всегда. Следовательно, если их вычисление громоздко, то желательно заранее выяснить их существование. Кроме того, бывают случаи, когда несобственный интеграл вообще нет необходимости вычислять, а требуется лишь знать, сходится он или нет. В этом случае используются теоремы о сходимости несобственных интегралов, основанные на сравнении исследуемого несобственного интеграла с известными.

Теорема 1. Пусть функци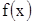и  и 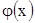 непрерывны на промежутке  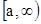и удовлетворяют неравенствам 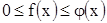. Тогда,

1) если интеграл 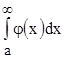 сходится, то сходится и интеграл ;

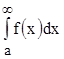2) если интеграл 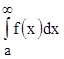 расходится, то расходится и интеграл .

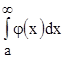Доказываем первую часть. Из неравенств 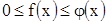, основываясь на свойствах неопределенных интегралов (свойство 5, п. 2), следует, что

 

,

 

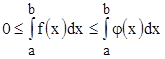где 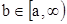. При увеличении верхнего предела интегрирования значения обоих интегралов будут непрерывно расти, так как подынтегральные функции по условию теоремы положительны. Следовательно, величины обоих интегралов будут функциями верхних пределов интегрирования. Перейдем к пределу в неравенствах, когда 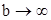. Согласно свойству 6 (п. 3.5) неравенства при этом не нарушатся:

 

.

 

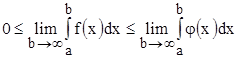По условию теоремы 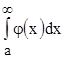 сходится, то есть 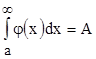. У интеграла  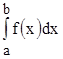величина будет монотонно расти с ростом 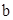. Однако эта монотонно возрастающая последовательность ограничена сверху числом 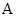. Следовательно, 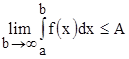, то есть несобственный интеграл  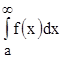сходится.

Во втором случае также из 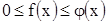 следует, что 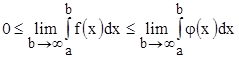. Но в этом случае  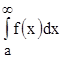по условию расходится, то есть 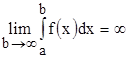. Тогда и 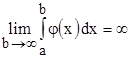, то есть несобственный интеграл  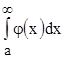расходится. Теорема доказана.

Для несобственных интегралов от разрывных функций существует аналогичная теорема.

 

Теорема 2. Пусть функци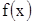и  и 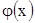 непрерывны на промежутке 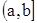, удовлетворяют неравенствам  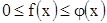и в точке  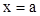одновременно терпят разрыв второго рода. Тогда,

1) если 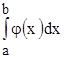 сходится, то  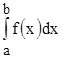сходится также;

2) если 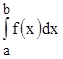 расходится, то расходится и .

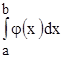Доказательство теоремы 2 проводится абсолютно так же, как и теоремы 1. Ниже соответствующие теоремы сходимости для несобственных интегралов от разрывных функций формулироваться не будут.

 

Теорема 3. Если на промежутке 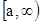 функция  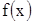меняет свой знак, то если  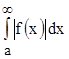сходится, то сходится и 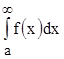, при этом второй интеграл называется абсолютно сходящимся.

Доказательство. Рассмотрим вспомогательную функцию 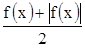. Очевидно, что она удовлетворяет неравенствам 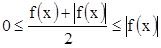. Согласно теореме 1 из сходимости  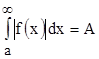следует сходимость 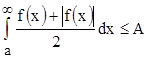. Но тогда  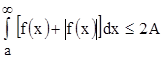и 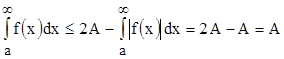. Следовательно, несобственный интеграл  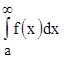сходится, что и требовалось доказать.

Аналогичная теорема имеет место и для несобственных интегралов от разрывных функций.

Теорема 4. Если положительные функци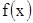и  и 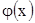 непрерывны на промежутке  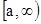и при этом 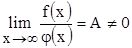, то оба несобственных интеграла  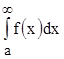и 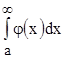 ведут себя одинаково.

Данную теорему доказывать не будем. Аналогичная теорема существует и для несобственных интегралов от разрывных функций, но при вычислении предела переменная 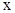 стремится к точке разрыва.

В заключение отметим, что в качестве известных или эталонных функций, упоминаемых в теоремах, часто используются функци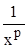и  и 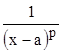 проинтегрированные в примерах параграфов 15 и 1

 

Литература

 

1. Бугров Я.С., Никольский С.М. ВЫСШАЯ МАТЕМАТИКА В 3-х томах Т. 1 Элементы линейной алгебры и аналитической геометрии 8-е изд. Изд-во: ДРОФА, 2006. – 284 с.

2. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М., «Наука», 1986.

3. Лобоцкая Н.Л. Основы высшей математики. Минск, «Высшая школа», 1973.

4. Минорский В.П. Сборник задач по высшей математики.

5. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109 с.

6. Никольский С.М., Бугров Я.С. ВЫСШАЯ МАТЕМАТИКА В 3-Х ТОМАХ Т. 2 Дифференциальное и интегральное исчисление 8-е изд. Изд-во: ДРОФА, 2007. – 509 с.

7. Олейник С.Н. Математический анализ в задачах и упражнениях. Несобственные интегралы и ряды Фурье. Изд-во: Факториал Пресс, 1998. – 488c.

8. Черненко В.Д. Высшая математика в примерах и задачах. В трех томах. ПОЛИТЕХНИКА, 2003.