Интегралом от функции комплексного переменного называется предел последовательности интегральных сумм; функция при этом определена на некоторой кривой l, кривая предполагается гладкой или кусочно-гладкой:
 , где
, где 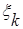 - точка, произвольно выбранная на дуге
- точка, произвольно выбранная на дуге  разбиения кривой,
разбиения кривой,  - приращение аргумента функции на этом участке разбиения,
- приращение аргумента функции на этом участке разбиения,  - шаг разбиения,
- шаг разбиения, 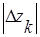 - длина хорды, соединяющей концы дуги
- длина хорды, соединяющей концы дуги  , кривая l разбивается произвольным образом на n частей
, кривая l разбивается произвольным образом на n частей  , k=1,2…n.
, k=1,2…n.
В случае замкнутой кривой l=C:

Интегрирование происходит в положительном направлении, т.е. в направлении обхода, оставляющем слева конечную область, ограниченную контуром C.
Существует несколько способов вычисления интегралов в комплексной области.
Способ 1. Интеграл вычисляется сведением к криволинейному интегралу от функции действительных переменных, применяются формулы:
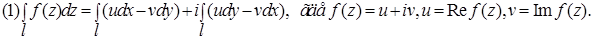 Пример 1. Вычислить интеграл
Пример 1. Вычислить интеграл 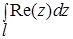 , где:
, где:
а). l – прямая, соединяющая точки 
б). l – ломаная ОВА, О(0,0), В(1,0), А(1,1).
Решение:
а). Путь интегрирования l – прямая, соединяющая точки 
Применяем к вычислению интеграла формулу (1). Подинтегральное выражение имеет вид 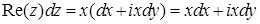 .
.
Поэтому:  .
.
Уравнение отрезка прямой, соединяющей точки  имеет вид
имеет вид 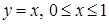 .
.
Получаем: 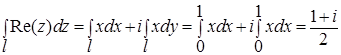 .
.
б). Путь интегрирования l – ломаная ОВА, О(0,0), В(1,0), А(1,1).
Так как путь интегрирования состоит из 2 отрезков, то:
 .
.
Каждый из этих двух интегралов вычисляем для ОВ ( ), и для ВА (
), и для ВА ( ).
).
Тогда  .
.
В пакете Mathematica (см. рисунок 3.6):

Рисунок 3.6 – Пример вычисления интеграла
Способ 2. Интеграл вычисляется приведением к определенному интегралу (путь интегрирования f задается в параметрической форме z=z(t)) – применяется формула:
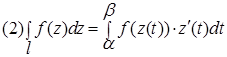 .
.
Пример 2. Вычислить интеграл  , l –верхняя полуокружность
, l –верхняя полуокружность  , обход l против часовой стрелки. Подинтегральная функция здесь непрерывная, но не аналитическая. Применим формулу (2), поскольку кривая l имеет простое параметрическое представление:
, обход l против часовой стрелки. Подинтегральная функция здесь непрерывная, но не аналитическая. Применим формулу (2), поскольку кривая l имеет простое параметрическое представление: 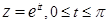 . Тогда
. Тогда  .
.
Подставляем в подинтегральное выражение:
 .
.
В пакете Mathematica (см. рисунок 3.7):

Рисунок 3.7 – Пример вычисления интеграла
Способ 3. Вычисление интегралов от аналитических функций в односвязных областях – применяется формула:
 , где F(z) первообразная для f(z).
, где F(z) первообразная для f(z).
Пример 3. Вычислить интеграл от аналитической функции  .
.
Применяем формулу (3), находим первообразную, используя методы интегрирования действительного анализа:
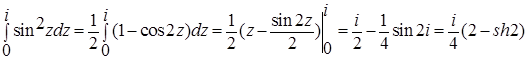 .
.
В пакете Mathematica (см. рисунок 3.8):

Рисунок 3.8 – Пример вычисления интеграла
 2020-01-14
2020-01-14 204
204








