Вычисление интеграла с помощью теоремы о вычетах

Теорема (основная теорема о вычетах):

Если функция f(z) – аналитична в 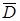 за исключением конечного числа особых точек  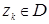,то справедливо равенство:

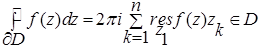, где D – односвязная область в комплексной плоскости,  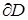- граница D,  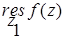- вычет функции f(z) в точке .

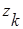Пример 1. Вычислить интеграл .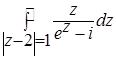

Особыми точками подинтегральной функции являются нули знаменателя – корни уравнения exp(z) – i =0, т.е. точки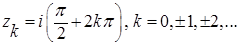

Кругу 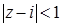 принадлежит только одна из этих точек, точка .

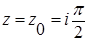Эта точка - простой полюс функции 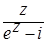, т.к. она является простым нулем знаменателя. Вычислим вычет в простом полюсе f(z):

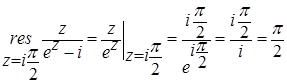. Тогда .

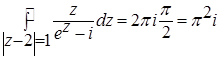В пакете Mathematica (см. рисунок 3.9):

Рисунок 3.9 – Пример вычисления интеграла

Пример 2. Вычислить интеграл .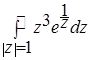

Единственная особая точка подинтегральной функции – существенно особая точка z=0. Она принадлежит области, ограниченной контуром интегрирования.

Вычислим вычет в существенно особой точке функции f(z): 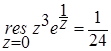, поскольку 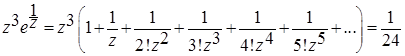. Тогда .

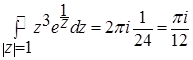В пакете Mathematica (см. рисунок 3.10):

Рисунок 3.10 – Пример вычисления интеграла

Пример 3. Вычислить интеграл .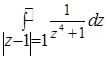

Особыми точками подинтегральной функции являются нули знаменателя – корни уравнения 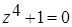, т.е. точки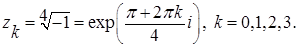

Все эти точки – простые полюсы подинтегральной функции, кругу 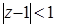 принадлежит только две из них: .

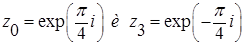Вычислим вычеты в этих точках:

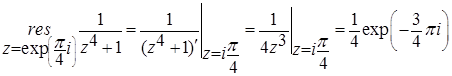
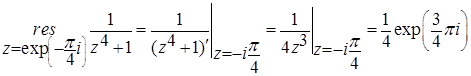
Тогда:

.

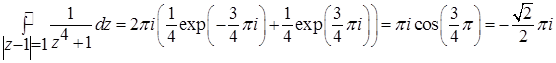В пакете Mathematica (см. пример 3.11):

Рисунок 3.11 – Пример вычисления интеграла