Полосовой фильтр Баттеруорта /12/

Как известно, полосовой фильтр можно получить непосредственной комбинацией низкочастотного и высокочастотного фильтра при перекрытии полосы пропускания фильтров. Аналогичный эффект достигается и частотным преобразованием ФНЧ, которое в этом случае имеет вид:

                                                   p = s+1/s.                                             (6.3.1)

Подставив в (6.3.1) значения p = jW и s = jw, получим:

W = [w²-1]/w,

                                                           w²-Ww-1 = 0.                                         (6.3.2)

Корни уравнения (6.3.2):

                                              (w)_1,2 = W/2 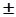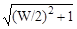.                              (6.3.3)

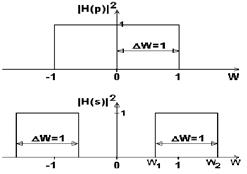
Расщепление спектра. При W=0 имеем w = 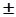1, т.е. центр полосы пропускания ФНЧ (от -W_с до +W_с) расщепляется на два (как и положено, для полосовых фильтров) и смещается в точки w = 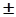1. Подставив в (6.3.3) граничную частоту W_с=1 нормированного ФНЧ, определяем граничные частоты нормированного полосового фильтра в виде пары сопряженных частот:

w₁ = 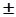0.618, w₂ = 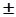1.618

Рис. 6.3.1. Расщепление полосы.

Сущность произведенного преобразования наглядно видна на рис. 6.3.1. Ширина полосы пропускания нормированного ПФ равна 1.

Полученное преобразование можно распространить на полосовой фильтр с ненормированными частотами w_н и w_в.

Введем понятие геометрической средней частоты фильтра w_о:

             w_о= 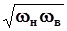.         (6.3.4)

Ширина полосы пропускания ПФ связана (см. рис.6.3.1) с граничной частотой ФНЧ соотношением:

Dw = w_в-w_н = w_с = w_н.

В долях средней геометрической частоты:

                                                      W_н = (w_в-w_н)/w_о = W_с.                                 (6.3.5)

Заменяя в (6.3.4-6.3.5) значение w_в на произвольную частоту w и подставляя в (6.3.5) значение ω_н = ω·ω_о²  из (6.3.4), получаем произвольную частоту W:

                                          W = (w-w_н)/w_о = w/w_o-w_o/w.                             (6.3.6)

Отсюда, в выражении (6.1.1) вместо нормированной частоты W = w/w_с можно применить функцию частоты полосового фильтра w(w):

w(w) = (w²-w_о²)/[w(w_в-w_н)],

или, подставляя (6.3.4) вместо ω_о:

    w(w) = (w²-w_нw_в)/[w(w_в-w_н)].                             (6.3.7)

Тем самым передаточная функция ФНЧ выражается в единицах, которые позволяют после применения преобразования (6.3.1) использовать для задания необходимые граничные частоты w_н и w_в полосового фильтра.

Пример расчета полосового фильтра Баттеруорта.

Техническое задание: 

- Шаг дискретизации данных Dt = 0.0005 сек.

Частота Найквиста f_N =  1/2Dt = 1000 Гц, ω_N = 6.283·10³ рад.

- Нижняя граничная частота полосы пропускания: f_н = 340 Гц, w_н = 2.136·10³ рад.

- Верхняя граничная частота полосы пропускания: f_в = 470 Гц, w_в = 2.953·10³ рад.

- Крутизна срезов в децибелах на октаву: К_р = 45.

Расчет параметров:

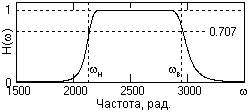
Рис. 6.3.2.

1. Порядок фильтра по формуле (6.1.6'): 

N = К_р/6 = 45/6 = 7.5.

Для расчетов принимаем N=8.

2. Строим график функции H(w) = 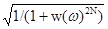 с использованием выражения (6.3.7). Передаточная характеристика фильтра приведена на рис. 6.3.2.

3. Деформированные частоты по формуле (6.1.4):

w_dн = 2.366·10³ рад. w_dв = 3.64·10³ рад. w_do = 2.934·10³.

Полосовой фильтр на s-плоскости. С учетом деформации частот, принимаем p = jw = j(w²-w_dнw_dв)/[w(w_dв-w_dн)], s= jω и заменяем ω = s/j в выражении р:

р = (s²+w_dнw_dв)/[s(w_dв-w_dн)],

                                          s²-p(w_dв-w_dн)s+w_dнw_dв = 0.                          (6.3.8)

Koрни уравнения (6.3.8) определяют местоположение полюсов ПФ:

                s = s* = p(w_dв-w_dн)/2 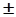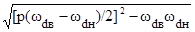.          (6.3.9)

Уравнение (6.3.9) показывает расщепление каждого p-полюса, определяемых выражением (6.1.14), на два комплексно сопряженных полюса s-плоскости, произведение которых будет давать вещественные биквадратные блоки в s-плоскости. При этом следует учесть то обстоятельство, что устойчивому рекурсивному фильтру на z-плоскости должны соответствовать полюса только одной (левой) половины p,s - плоскостей.

Передаточная функция. При применении преобразования (6.3.1) к передаточной функции в полиномиальной форме (6.1.11), получаем:

                              H(p) = G 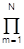1/(p-p_m) ó G 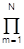s/(s²-p_m s+1) =  H(s),          (6.3.10)

       Выражение (6.3.10) не требует нахождения полюсов, т.к. они уже известны и определяются выражением (6.3.9). С учетом этого функция H(s) может быть записана с объединением в биквадратные блоки комплексно сопряженных полюсов с вещественными коэффициентами:

H(s) = G 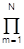s/[(s-s_m)(s-s*_m)] = G 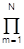s/(s²+a_m s+g_m),             (6.3.11)

где значения а_m и g_m могут быть определены непосредственно по полюсам (6.3.9):

a_m = -2 Re s_m,  g_m = (Re s_m)² + (Im s_m)² = |s_m|².         (6.3.12)

Продолжение расчета фильтра Баттеруорта.

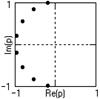
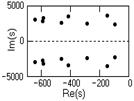
Рис. 6.3.3.                 Рис. 6.3.4.

4. Полюса фильтра на единичной окружности

в р-плоскости:

p_n = j·exp[j·p(2n-1)/2N], n = 1,2,…,N.

Положение полюсов приведено на рис. 6.3.3.

5. Полюса в левой половине s-плоскости, n = 1,2,…,2N

(приведены на рис. 6.3.4):

.

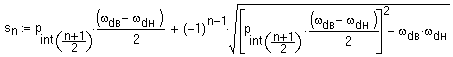6. По полученным значениям полюсов вычисляем коэффициенты a_m и g_m (6.3.12), m = n.

a_m = 196.8, 300.4, 581.2, 834.5, 930.5, 1188, 1196, 1304.

g_m = 5.64·10⁶, 1.314·10⁷, 5.997·10⁶, 1.236·10⁷, 6.742·10⁶, 1.1·10⁷, 7.895·10⁶, 9.39·10⁶. 

По приведенному примеру можно заметить, что при использовании ненормированных частот w, достаточно существенных по своей величине, значения s-полюсов и, соответственно, величины коэффициентов а_m и g_m имеют большие порядки, что нежелательно для дальнейших расчетов и может приводить к появлению погрешностей при ограничении разрядности. Для исключения этого фактора значения полюсов s_n рекомендуется пронормировать на среднюю геометрическую частоту:

s_n = s_n/w_o.

Продолжение расчета фильтра Баттеруорта.

6'. Значения коэффициентов a_m и g_m (6.3.12), вычисленные по нормированным значениям s_n.

a_m = 0.067, 0.102, 0.198, 0.284, 0.317, 0.405, 0.407, 0.444.

g_m = 0.655, 1.527, 0.697, 1.436, 0.783, 1.277, 0.917, 1.091. 

Коэффициент g билинейного преобразования для ненормированных значений w и полюсов s_n имеет классическую форму: g = 2/Dt. Соответственно, для нормированных значений: g = 2/(Dt·w_o). После билинейного z-преобразования выражения (6.3.11), получаем:

                              H(z) = G 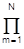G_m (1-z²)/(1-b_m z+c_m z²).                           (6.3.13)

G_m = 1/(g+a_m+g_mg^-1.                                       (6.3.14)

                                     b_m = 2G_m(g-g_mg^-1).                                          (6.3.15)

                                     c_m = G_m(g-a_m+g_mg^-1.                                       (6.3.16)

Продолжение расчета фильтра Баттеруорта (по нормированным полюсам s_n).

7. Значения коэффициента g: g = 1.363.

8. Значения коэффициентов G_m по (6.3.14):

G_m = 0.523, 0.387, 0.483, 0.37, 0.444, 0.37, 0.409, 0.384.

9. Значения коэффициентов b_m по (6.3.15):

b_m = 0.924, 0.188, 0.823, 0.23, 0.7, 0.315, 0.565, 0.432.

10. Значения коэффициентов c_m по (6.3.16):

c_m = 0.93, 0.921, 0.809, 0.789, 0.719, 0.701, 0.666, 0.659.

11. Общий нормировочный множитель G: G = 1.264·10^-3.

12. Заключительная передаточная функция:

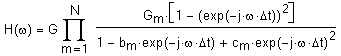
  При построении графика данной функции можно убедиться, что она полностью соответствует рисунку 6.3.2.

13. Уравнение одной секции фильтра:

y_m,k = G_m·(y_m-1,k - y_m-1,k-2) + b_m y_m,k-1 – c_m y_m,k-2 .

Разные значения множителей G_m в секциях фильтра обычно опускаются и нормировкой H(z) к 1 на геометрической средней частоте фильтра определяют общий множитель G, что ускоряет вычисления:

G = 1/H(exp(-jDtw_o)).                                     (6.3.17)

При очень малой величине порядка значения G для исключения и накопления аппаратных ошибок вычислений можно применять и другой метод: устанавливать для всех секций постоянное значение G_m = const, такое, при котором G = 1.

Если применить обратное частотное преобразование p = s(w_в-w_н)/(s²+w_в w_н), то в результате будет получен полосовой заградительный фильтр.