Структура оптимального решающего правила

Рассмотрим структуру правила, оптимального по весовому критерию (под структурой решающего правила понимается последовательность математических и логических операций, которые необходимо выполнить над выборочными значениями , чтобы вынести требуемое решение).

В соответствии с весовым критерием мы должны найти правило, обеспечивающее выполнение условия , где  - весовой множитель.

Запишем вероятности  и  в виде

; .

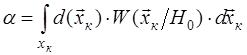Здесь  - многомерные плотности вероятности (функции правдоподобия) выборки  при наличии и отсутствии сигнала (обратите внимание на различие в обозначениях дифференциала  и решающего правила ).

Весовой критерий при этом может быть представлен в виде , где  - отношение правдоподобия выборки . Чтобы выполнить условие максимума интеграла, достаточно за счет соответствующего выбора решающей функции  добиться для каждого из возможных значений  наибольшего значения подынтегральное выражения. Эта функция в нашем случае принимает только два значения: 0 и 1, так что подынтегральное выражение либо обращается в нуль, либо умножается на единицу. Следовательно, максимум интеграла достигается, если для положительных значений подынтегрального выражения принимать , а для отрицательных  - т.е.

Таким образом, оптимальный в смысле весового критерия обнаружитель представляет устройство вычисления отношения правдоподобия наблюдаемой выборки и сравнения его с фиксированным порогом .

Отношение правдоподобияя, т.е. отношение функций правдоподобия , показывающее, какую из двух взаимоисключающих гипотез (ситуаций) -  или  следует считать более вероятной, играет фундаментальную роль в теории различения статистических гипотез, поскольку представляет важнейший случай решающей статистики.

Решающей статистикой (не путать со статистикой, как областью математической и экономической наук) называют функцию выборочных значений, размерность которой меньше, чем у исходной выборки. Очевидно, что чем меньше размерность решающей статистики, тем проще ее использовать для построения решающего правила. Наилучшей с этой точки зрения является одномерная статистика, например, выборочное среднее  или выборочные моменты более высоких порядков. Однако сокращение размерности (редукция) выборочных данных не должно приводить к потере содержащейся в выборке полезной информации, на основании которой решается задача различения статистических гипотез. Статистика, обладающая таким свойством, называется достаточной; среди достаточных статистик наибольший интерес представляет минимальная достаточная статистика, т.е. статистика минимальной размерности, при которой свойство достаточности еще сохраняется. Доказано, что в том случае, когда элементы выборки  как при гипотезе, так и при альтернативе статически независимы, отношение правдоподобия является минимальной достаточной статистикой при различении простых гипотез. (Напомним, что необходимым и достаточным условием независимости выборочных значений является факторизация функций правдоподобия, т.е. возможность их представления в виде ).

В более общем случае это свойство отношения правдоподобия может нарушаться, однако и в этом случае квазиоптимальные алгоритмы часто используют статистику отношения правдоподобия.

Можно также показать, что в случае различения простых гипотез полученная структура обнаружителя – “вычислитель отношения правдоподобия + постоянный порог” - является оптимальной не только весового критерия, но и для других, рассмотренных нами: Неймана-Пирсона, максимума апостериорной вероятности, максимального правдоподобия, минимаксного. Различие этих критериев выражается только в величине порога .

Очевидно, что для рассмотренной структуры решающего правила его оптимальность не нарушится, если отношение правдоподобия заменить любой монотонной однозначной функцией от него (при условии соответствующего пересчета значения решающего порога). Часто в качестве такой функции используют логарифм отношения правдоподобия . Переход к этой статистике удобен при независимых выборках, когда функции правдоподобия факторизуется. При этом , соответственно , т.е. при вычислении решающей статистики операция умножения заменяется существенно более простой операцией суммирования.

Самостоятельную роль в теории принятия статистических решений играет математическое ожидание логарифма отношения правдоподобия  (информация Кульбака-Леблера). Величина  может служить количественной мерой статистического “расстояния” между различаемыми распределениями. Смысл этой величины достаточно нагляден: чем больше площадь перекрытия одномерных функций правдоподобия  и , тем ближе к нулю (в среднем) логарифм отношения правдоподобия и наоборот, чем меньше площадь перекрытия кривых , тем большую модуль информация Кульбака-Леблера. Величина  может интерпретироваться как среднее приращение статистики  на один элемент выборки (шаг наблюдения) в процессе ее накопления, поэтому средний объем выборки, необходимый для вынесения решения с заданными вероятностями ошибок a и b, обратно пропорционален этой величине (подробнее см. следующие разделы).

Необходимо подчеркнуть. Что операция расчета логарифма отношения правдоподобия может реализовываться с помощью устройств согласованной фильтрации (известно, что выходной эффект фильтра, согласованного с наблюдаемой выборкой, пропорционален логарифму отношения правдоподобия этой выборки). На практике оптимальная обработка выборки обычно разделяется на два этапа: согласованную фильтрацию одиночногосигнала и расчет отношения правдоподобия для последовательностиотсчетов, наблюдаемых на выходе согласованного фильтра. Поэтому мы под формированием решающей статистики будем понимать расчет отношения правдоподобия (или его логарифма) для выборки, наблюдаемой навыходефильтра (коррелятора) согласованного с одиночным сигналом.