Проведем расчет отношения правдоподобия при простых гипотезах, когда соответствующие функции правдоподобия 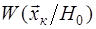 ;
; 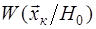 не содержат неизвестных параметров. Рассмотрим случай обнаружения сигнала с известной амплитудой
не содержат неизвестных параметров. Рассмотрим случай обнаружения сигнала с известной амплитудой 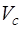 и начальной фазой
и начальной фазой 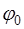 . (Для радиолокации этот случай является идеализированным, т.к. соответствует обнаружению цели с известной ЭПР, находящейся на известной дальности и обладающей известной радиальной скоростью. Однако такая модель сигнала наиболее наглядна, а также служит исходной для других, более сложных моделей, рассматриваемых ниже.)
. (Для радиолокации этот случай является идеализированным, т.к. соответствует обнаружению цели с известной ЭПР, находящейся на известной дальности и обладающей известной радиальной скоростью. Однако такая модель сигнала наиболее наглядна, а также служит исходной для других, более сложных моделей, рассматриваемых ниже.)
В качестве помехи, присутствующей на выходе оптимального приемника будем рассматривать узкополосный гауссовский шум, среднеквадратическое отклонение которого s также считается известным. Для удобства будем рассматривать амплитуды принятого и расчетного сигналов, нормированные относительно с.к.о. шума: 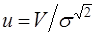 ;
; 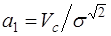 .
.
Известно, что оптимальный фильтр такого сигнала представляет собой коррелятор, на опорный вход которого подается полная (с точностью до начальной фазы 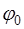 ) копия ожидаемого сигнала. Напряжение на выходе коррелятора описывается совокупностью отсчетов его огибающей
) копия ожидаемого сигнала. Напряжение на выходе коррелятора описывается совокупностью отсчетов его огибающей 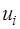 и фазы
и фазы 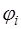 относительно опорного гармонического колебания, синфазного с сигналом.
относительно опорного гармонического колебания, синфазного с сигналом.
Соответствующие гипотезам 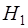 и
и 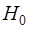 совместные плотности распределения отсчетов огибающей и фазы для выборки, содержащей
совместные плотности распределения отсчетов огибающей и фазы для выборки, содержащей 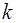 пар отсчетов, можно записать в виде:
пар отсчетов, можно записать в виде:
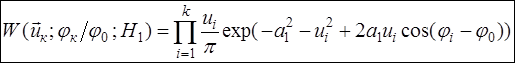 (2.1)
(2.1)
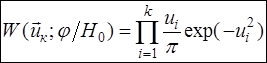 (2.2).
(2.2).
Соответственно, отношение правдоподобия и его логарифм
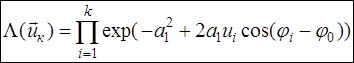 ,
, 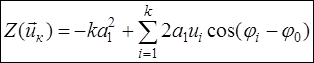 .
.
Последнее выражение определяет функциональное преобразование, которому должны подвергаться отсчеты амплитуды и фазы на выходе согласованного фильтра при расчете логарифма отношения правдоподобия выборки (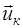 ).
).
На практике для удобства в качестве выходного эффекта оптимального фильтра обычно рассматривают напряжение на выходе амплитудно-фазовогодетектора 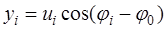 .
.
Очевидно, что в этом случае 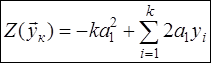 . (3.3)
. (3.3)
Рассчитаем математическое ожидание статистики (2.3), т.е. ее среднее приращение (информацию Кульбака-Леблера), приходящееся на один отсчет 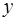 .
.
Используя известную формулу плотности вероятности произведения двух случайных величин, нетрудно убедиться, что при наличии сигнала величина 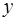 имеет нормальное распределение:
имеет нормальное распределение:
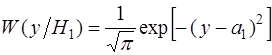 (2.4)
(2.4)
мат. ожидание которого 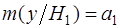 , а дисперсия
, а дисперсия 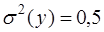 . При нулевой гипотезе (
. При нулевой гипотезе (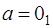 ) мат. ожидание
) мат. ожидание 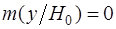 , дисперсия не меняется. Поскольку преобразование (2.3) линейно относительно
, дисперсия не меняется. Поскольку преобразование (2.3) линейно относительно 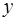 можно утверждать, что распределение решающей статистики
можно утверждать, что распределение решающей статистики 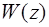 также нормально с параметрами:
также нормально с параметрами:
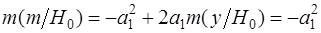 ;
; 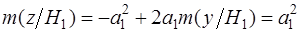 ;
; 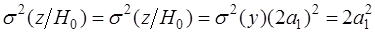 (2.5)
(2.5)
Таким образом, для полностью известного сигнала абсолютная величина информации Кульбака-Леблера при гипотезе и альтернативе одинакова и равна квадрату эффективного значения 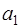 .
.
 2020-01-14
2020-01-14 155
155







