Основные теоремы теории вероятности

Содержание

Основные понятия теории вероятности

Случайная величина

Основные теоремы теории вероятности

Случайные величины и их законы распределения

Библиографический список

Основные понятия теории вероятности

Полная группа событий: несколько событий образуют полную группу, если в результате опыта непременно должно появиться хотя бы одно из них.

Несовместные события: несколько событий являются несовместными в данном опыте, если никакие два из них не могут появиться вместе.

Равновозможные события: несколько событий называются равновозможными, если есть основание считать, что ни одно из них не является предпочтительным по сравнению с другими.

Частота события: если производится серия из N опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частотой события А в данной серии опытов называется отношение числа опытов, в которых появилось событие А, к общему числу произведенных опытов.

Частоту события часто называют статистической вероятностью и вычисляют на основании результатов опыта по формуле , где m – число появлений события А.

При небольшом числе опытов N частота может меняться от одной серии опытов к другой из-за случайности событий. Однако при большом числе опытов она носит устойчивый характер и стремится к значению, которое называется вероятностью события.

 

Случайная величина

Случайной величиной (СВ) называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

Примеры: число попаданий в мишень при ограниченном числе выстрелов; число вызовов по телефону в единицу времени; количество некондиционных транзисторов в партии выпускаемых изделий и т.д.

Случайные величины, принимающие только отдельные значения, которые можно пересчитать, называются дискретными случайными величинами.

Существуют СВ другого типа: значения шумового давления, измеренного в различные моменты времени; вес булки хлеба, продаваемого в магазине и т.д. Называют их непрерывными случайными величинами.

 

Основные теоремы теории вероятности

Сумма и произведение событий. Суммой двух событий А и Б называется событие С, состоящее в выполнении события А, или события Б, или обоих вместе.

Например, если событие А – попадание в мишень при первом выстреле, событие Б – попадание в мишень при втором выстреле, то событие С = А + Б есть попадание в мишень вообще безразлично при каком выстреле – при первом, при втором или при обоих вместе.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Произведением двух событий А и Б называется событие С, состоящее в совместном выполнении события А и события Б.

Если производится два выстрела по мишени и если событие А есть попадание при первом выстреле, а событие Б – попадание при втором выстреле, то С = А∙Б есть попадание при обоих выстрелах.

Произведением нескольких событий называется событие, состоящее в совместном появлении всех этих событий.

2. Теорема сложения вероятностей. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

 

.

Пусть возможные исходы опыта сводятся к совокупности случаев, которые для наглядности представлены на рис. 1 в виде N символов.

 

Рис. 1

 

Предположим, что из этих случаев m благоприятны событию А, а k – событию Б. Тогда

 

.

 

Так как события А и Б несовместны, то нет случаев, которые благоприятны событиям А и Б вместе. Следовательно, событию А + Б благоприятны m + k случаев и

 

.

 

Подставляя полученные выражения в формулу для вероятности суммы двух событий, получим тождество.

Следствие Если события А ₁, А ₂, …, А_N образуют полную группу событий, то сумма их вероятностей равна единице.

Следствие 2. Сумма вероятностей противоположных событий равна единице.

3. Теорема умножения вероятностей. Необходимо ввести понятия независимых и зависимых событий.

Событие А называется независимым от события Б, если вероятность события А не зависит от того, произошло событие Б или нет.

Событие А называется зависимым от события Б, если вероятность события А меняется от того, произошло событие Б или нет.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается P (А / В).

Теорема умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:

 

.

 

Пусть возможные исходы опыта сводятся к N случаям, которые для наглядности даны в виде символов на рис. 2.

 

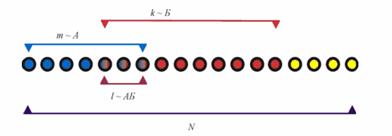
Рис. 2

 

Предположим, что событию А благоприятны m случаев, а событию Б – k случаев. Так как не предполагались события А и Б совместными, то существуют случаи, благоприятные и событию А, и событию Б одновременно. Пусть число таких случаев l. Тогда P (АБ) = l / N; P (A) = m / N. Вычислим P (Б / А), т.е. условную вероятность события Б в предположении, что А имело место. Если известно, что событие А произошло, то из произошедших N случаев остаются возможными только те из m, которые благоприятствовали событию А. Из них l случаев благоприятны событию Б. Следовательно, P (Б / А) = l / m. Подставляя выражения P (АБ), P (A) и P (Б / А) в формулу вероятности произведения двух событий, получим тождество.

Следствие Если событие А не зависит от события Б, то и событие Б не зависит от события А.

Следствие 2. Вероятность произведения двух независимых событий равна произведению этих событий.

4. Формула полной вероятности. Формула полной вероятности является следствием обеих теорем – теоремы сложения вероятностей и теоремы умножения вероятностей.

Пусть требуется определить вероятность некоторого события А, которое может произойти вместе с одним из событий H ₁, H ₂,…, H_N, образующих полную группу несовместных событий. Будем эти события называть гипотезами. Тогда

 

,

 

т.е. вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Эта формула носит название формулы полной вероятности.

Так как гипотезы H ₁, H ₂,…, H_N образуют полную группу событий, то событие А может появиться только в комбинации с какой-либо из этих гипотез: А = H ₁ А + H ₂ А + …+ H_NА. Так как гипотезы H ₁, H ₂,…, H_N несовместны, то и комбинации H ₁ А, H ₂ А, … H_NА также несовместны. Применяя к ним теорему сложения, получим:

 

.

 

Применяя к событию H_iА теорему сложения, получим искомую формулу.

5. Теорема гипотез (формула Байеса). Имеется полная группа несовместных гипотез H ₁, H ₂,…, H_N. Вероятности этих гипотез до опыта известны и равны соответственно P (H ₁), P (H ₂), …, P (H_N). Произведем опыт, в результате которого будет наблюдаться появление некоторого события А. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события?

Здесь, по существу, идет речь о том, как найти условную вероятность  для каждой гипотезы после проведения эксперимента.

Из теоремы умножения имеем:

 

, (i = 1, 2, …, N).

 

Или, отбрасывая левую часть, получим

 

, (i = 1, 2, …, N),

 

откуда

 

, (i = 1, 2, …, N).

 

Выражая P (А) с помощью формулы полной вероятности, имеем:

 

, (i = 1, 2, …, N).

 

Эта формула и носит название формулы Байеса или теоремы гипотез. Используется она в теории проверки статистических гипотез (в частности, в теории обнаружения сигналов на фоне помех).