2020-01-14
179
Неравенства вида (или меньше) при а (х) >0 и решаются на основании свойств показательной функции: для 0 < а (х) < 1 при сравнении f (x) и g (x) знак неравенства меняется, а при а (х) > 1 - сохраняется. Самый сложный случай при а (х) < 0. Здесь можно дать только общее указание: определить, при каких значениях х показатели f (x) и g (x) будут целыми числами, и выбрать из них те, которые удовлетворяют условию. Наконец, если исходное неравенство будет выполняться при а (х) = 0 или а (х) = 1 (например, когда неравенства нестрогие), то нужно рассмотреть и эти случаи.
Логарифмы и их свойства
Логарифм числа b по основанию a (от греч. λόγος - "слово", "отношение" и ἀριθμός - "число" [1] ) определяется как показатель степени, в которую надо возвести основание a, чтобы получить число b. Обозначение: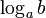 
. Из определения следует, что записи 
и 
равносильны. Пример: 
, потому что 
. Свойства
Основное логарифмическое тождество: 
Логарифмическая функция, её свойства и графики.
|
|
|
Логарифмической функцией называется функция вида f (x) = log ax, определённая при 
Область определения: 
Область значения: 
График любой логарифмической функции проходит через точку (1; 0)
Производная логарифмической функции равна:
