· Вчитель ставить перед класом питання: ”Як можна визначити положення точки на площині?”. Бесіду потрібно побудувати так, щоб учні назвали якомога більше прикладів: гра „Морський бій”, шахова дошка, розміщення місць у кінотеатрі, знаходження об’єкта на географічній карті тощо. Підсумком такої бесіди повинна бути відповідь на питання: „Скільки потрібно координат, щоб визначити чи задати положення точки на площині?”.
· Вчитель повідомляє тему і мету уроку.
· Перегляд слайдів. Під час перегляду кожен слайд супроводжується відповідними коментарями з боку вчителя. Учні, переглядаючи слайди, записують в робочі зошити повідомлення із позначкою „ !: ” та будують систему координат, в якій позначають координатні чверті, а також запропоновані точки.
 | |||||||||||
|
| ||||||||||
 | |||||||||||
|
| ||||||||||
 | |||||||||||
| |||||||||||
| |||||||||||
 | |||||||||||
 | |||||||||||
|
| ||||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||
| |||||||||||
 |  |
· Після перегляду слайду №8 необхідно зробити паузу і виконати кілька вправ для очей. Наприклад: сконцентрувати погляд на будь-якому далекому предметі за вікном, а потім на предметі, що знаходиться у класі, і так кілька разів.
· Після фізпаузи для очей учням пропонується коротеньке повідомлення про життя та наукову діяльність великого французького математика Рене Декарта.
IV. Осмислення нового матеріалу.
· Усне розв’язування вправ №699-701.
· Колективне розв’язування вправ №702, №708.
V. Домашнє завдання
№707, №710, №716
Додаток 3
Алгебра 7
Брейн-ринг
Тема: Розкладання многочленів на множники.
Мета: Узагальнити навчальний матеріал по темі „Розкладання многочленів на множники”, підготувати учнів до тематичної контрольної роботи.
Обладнання: комп’ютерний клас, пристрій для засвічування ліхтарів, набір питань оформлених у вигляді web-сторінки.
Хід уроку
Організаційна частина.
1. Поділ на команди
2. Призначення капітанів команд
3. Ознайомлення із правилами проведення гри
4. Розміщення команд за схемою
|
|
|
|
|
|
 (мал. 1).
(мал. 1).
|
Змагання.
|
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 |
Мал. 2
Питання 1 Питання 2
 |
Питання 3 Питання 4
 |  | ||
Питання 5 Питання 6
 | |||
 | |||
Питання 7
 | |||
 | |||
Питання 8
 |
Питання 9
 |
Питання 10
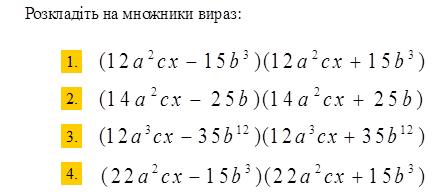 |
Питання 11 Питання 12

 |
Питання 13 Питання 14
 | |||
| |||
Питання 15 Питання 16
 | 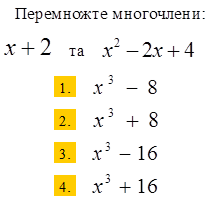 | ||
Питання 17 Питання 18
 | |||
 | |||
Питання 18 Питання 19
 | |||
| |||
Питання 20 Питання 21
 |  | ||
Питання 22 Питання 23
 | |||
 | |||
Питання 24 Питання 25
 | |||
 | |||
Підсумки змагань.
| №№ | № правильної відповіді | Відповіді до запитань брейн-рингу |
| 1 | 3 | 
|
| 2 | 3 | 
|
| 3 | 4 | 0;3 |
| 4 | 1 | 
|
| 5 | 2 | Немає розв’язків |
| 6 | - | Такої формули не існує |
| 7 | 4 | 
|
| 8 | - | Спосіб групування |
| 9 | 3 | 
|
| 10 | 1 | 
|
| 11 | 3 | 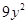
|
| 12 | 4 | 
|
| 13 | - | Бевз Григорій Петрович |
| 14 | 1 | 
|
| 15 | - | ...добутку суми і різниці цих виразів |
| 16 | 2 | 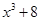
|
| 17 | 2 | 
|
| 18 | 3 | 
|
| 19 | - | §16 |
| 20 | 3 | 
|
| 21 | 4 | -4;0;4 |
| 22 | 1 | 
|
| 23 | 1 | так |
| 24 | 2 | ні |
| 25 | 3 | 
|
 2020-01-14
2020-01-14 111
111








