Точечна оцінка параметрів розподілу
Є два підходи до оцінювання невідомих параметрів розподілів по спостереженнях: точечний і інтервальний. Точечний вказує лише точку, біля якої знаходиться оцінюваний параметр; при інтервальному знаходять інтервал, що з деякою великою ймовірністю, що задається дослідником, накриває невідоме числове значення параметра. У главі розглядаються методи точечного оцінювання параметрів; будуються інтервальні оцінки параметрів нормального розподілу, обговорюється загальний підхід до інтервального оцінювання параметрів розподілу, відмінних від нормального.
Метод моментів
Метод моментів є одним із методів точечного оцінювання параметрів розподілу.
Нехай закон розподілу випадкової величини X відомий із точністю до числових значень його параметрів 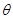 1,
1, 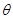 2,…,
2,…, 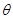 k. Це означає, що відомий вид функції щільності fx(х,
k. Це означає, що відомий вид функції щільності fx(х, 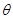 ), де
), де 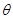 = (
= (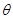 1,
1, 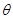 2,…,
2,…, 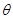 k ), якщо X безперервна (відомий вид функції ймовірності Р (X = х,
k ), якщо X безперервна (відомий вид функції ймовірності Р (X = х, 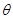 ), якщо X дискретна), але числові значення k параметрів не відомі. Знайдемо оцінку
), якщо X дискретна), але числові значення k параметрів не відомі. Знайдемо оцінку 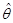 = (
= (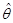 1,
1, 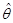 2,…,
2,…, 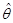 k ) параметра 0, розташовуючи вибіркою: х1, х2..., хп.
k ) параметра 0, розташовуючи вибіркою: х1, х2..., хп.
Допустимо, що існує k початкових моментів, кожний із який можна висловити через 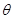 (без обмеження спільності можна розглядати тільки початкові моменти, тому що центральні моменти є функціями початкових). Нехай такими моментами будуть перший, другий,..., k-й: v1, v2,…,vk (що зовсім не обов'язково). Висловимо кожний із них через
(без обмеження спільності можна розглядати тільки початкові моменти, тому що центральні моменти є функціями початкових). Нехай такими моментами будуть перший, другий,..., k-й: v1, v2,…,vk (що зовсім не обов'язково). Висловимо кожний із них через 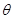 :
:
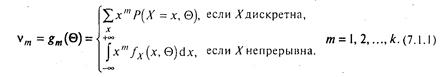 (3.1)
(3.1)
Помітимо, що в системі
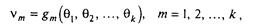 (3.2)
(3.2)
число рівнянь повинно бути рівним числу k оцінюваних параметрів. Знайдемо рішення системи (3.2). Висловивши кожний параметр q через v1, v2,…,vk, одержимо:
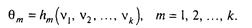 (3.3)
(3.3)
Властивість змістовності вибіркових початкових моментів є підставою для заміни в рівняннях (3.3) теоретичних моментів v1, v2,…,vk на обчислені при великому п вибіркові моменти v1, v2,…,vk.
Оцінками методу моментів параметрів 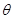 1,
1, 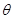 2,…,
2,…, 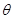 k називаються оцінки
k називаються оцінки
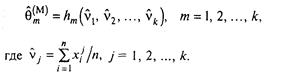 (3.4)
(3.4)
Питання про те, які початкові моменти включати в систему (3.2), варто вирішувати, керуючись конкретними цілями дослідження і порівняльної простоти форм залежностей моментів від параметрів. У статистичній практиці справа рідко доходить навіть до четвертих моментів.
Приклад 3.1.1 Випадковий розмір Х~ N (а, σ), при цьому числові значення параметрів а і σ 2 не відомі. Знайдемо оцінки методу моментів для цих параметрів.
Використовуючи формулу (3.1), висловимо моменти v1 і v2 через а й σ 2:
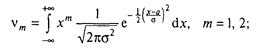
(v1 =a)∩(v2 = а2 + σ 2)- такий вид системи (3.2) у даному прикладі. Вирішивши її щодо а й σ 2, одержимо: а = v1 σ 2 = v2 - v1 2. Звідси оцінки методу моментів:
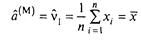
це оцінка математичного чекання а;
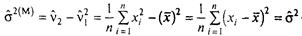
це оцінка дисперсії σ 2.
Відзначена раніше деяка невизначеність вибору початкових моментів може привести до одержання різних оцінок того самого параметра.
Приклад 3.1.2 Випадковий розмір X має розподіл Пуассона:
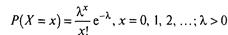
Знайдемо оцінку параметра X для двох
варіантів:
а) у якості початкового моменту візьмемо v1, одержимо:
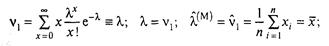
б) у якості початкового моменту візьмемо v2; одержимо:
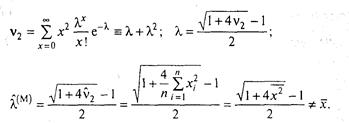
Оцінки - різні. Звичайно, краще перша: А, = х як більш проста і відповідному змісту параметра пуассонівського розподілу:
l = MX, тому за А, природно прийняти х - гарну точечну оцінку математичного чекання.
Однак не всі одержувані методом моментів оцінки мають властивості «гарної оцінки». Так, отримана в прикладі 3.1.1 оцінка
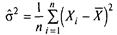
дисперсії σ 2 не має властивість незміщеності а є асимптотично незміщеною оцінкою: lim 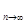 мd
мd 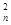 = lim
= lim 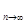 n-1/n*
n-1/n* 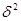
 =
= 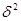 , тобто при великих п можна вважати, що
, тобто при великих п можна вважати, що 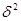 не зміщена щодо
не зміщена щодо 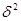 .
.
Приведемо без доказу теорему про функції від моментів, із якої випливають визначені властивості оцінок методу моментів.
Припустимо, що 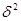 є функцією двох вибіркових моментів vk і vm:
є функцією двох вибіркових моментів vk і vm: 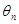 =h(v
=h(v 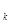 ,vm), що не містить явно п. Позначимо
,vm), що не містить явно п. Позначимо 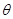 = h(v
= h(v 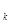 ,vm), де vk =Mvk, a vm = M/vm (останні дві рівності вірні в силу властивості незміщенності вибіркових початкових моментів),
,vm), де vk =Mvk, a vm = M/vm (останні дві рівності вірні в силу властивості незміщенності вибіркових початкових моментів),
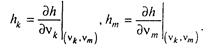


Теорема стверджує: якщо в деякій околиці точки (v 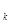 ,vm), функція h безперервна зі своїми першими і другими похідними, то при великих п розподіл випадкового розміру
,vm), функція h безперервна зі своїми першими і другими похідними, то при великих п розподіл випадкового розміру 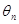 =h(v
=h(v 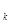 ,vm) близько до нормального (
,vm) близько до нормального (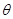 n має асимптотично нормальний розподіл) із математичним чеканням, рівним В, і дисперсією, рівної
n має асимптотично нормальний розподіл) із математичним чеканням, рівним В, і дисперсією, рівної
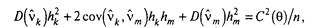 (3.5)
(3.5)
де С2(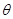 ) — деяка постійна, що залежить від
) — деяка постійна, що залежить від 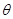 . (Теорему можна поширити на будь-яку кількість моментів — аргументів функції h)
. (Теорему можна поширити на будь-яку кількість моментів — аргументів функції h)
З теореми випливає, що при виконанні досить загальних умов оцінка методу моментів 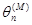 ), при великих п задовольняє наступним співвідношенням:
), при великих п задовольняє наступним співвідношенням:
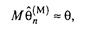 (3.6)
(3.6)
тобто оцінка методу моментів є асимптотично незміщенною,
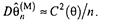 (3.7)
(3.7)
Переконаємося в тому, що 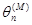 має властивість забезпеченості. Дійсно, нерівність Чебішева для розміру
має властивість забезпеченості. Дійсно, нерівність Чебішева для розміру 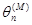 при великих п, прийме вид:
при великих п, прийме вид:
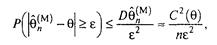
звідси одержимо, що при п - 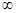 P(/
P(/ 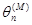 -
- 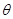 /<
/< 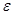 )
) 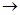 1.
1.
Уведемо поняття ефективності й асимптотичної ефективності незміщеної оцінки скалярного параметра 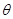 .
.
Ефективністю е(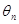 ) незміщеної оцінки
) незміщеної оцінки 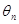 параметра
параметра 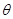 називають відношення min DQn(
називають відношення min DQn( 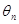 є s)— мінімально можливого значення дисперсії оцінки в класі S всіх незміщених оцінок параметра
є s)— мінімально можливого значення дисперсії оцінки в класі S всіх незміщених оцінок параметра 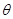 до дисперсії D
до дисперсії D 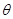 n розглянутої оцінки. При виконанні функцією щільно сті fх(х, 0) [функцією імовірності Р(Х =х,
n розглянутої оцінки. При виконанні функцією щільно сті fх(х, 0) [функцією імовірності Р(Х =х, 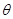 )] досить загальних умов регулярності: дифференційованих по
)] досить загальних умов регулярності: дифференційованих по 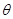 , незалежності області визначення від
, незалежності області визначення від 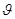 і т. д. — має місце нерівність Рао—Крамера—Фреше:
і т. д. — має місце нерівність Рао—Крамера—Фреше:
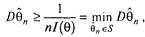 (3.8)
(3.8)
де i(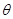 ) — кількість інформації про параметр
) — кількість інформації про параметр 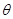 , що міститься в одиничному спостереженні, визначається співвідношенням
, що міститься в одиничному спостереженні, визначається співвідношенням
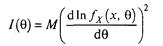 (3.9)
(3.9)
(i(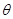 ) — деяка постійна, що залежить від
) — деяка постійна, що залежить від 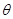 ). Тому
). Тому
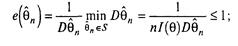 (3.10)
(3.10)
якщо е(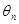 ) = 1, то
) = 1, то 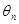 — ефективна оцінка параметра
— ефективна оцінка параметра 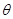 у класі S усіх
у класі S усіх
його незміщенних оцінок.
Асимптотичної ефективністю оцінки 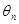 називають розмір
називають розмір
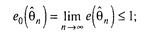 (3.11)
(3.11)
якщо 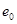 (
(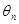 ) = 1 то
) = 1 то 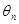 — асимптотична ефективна оцінка (очевидно, що ефективна оцінка буде й асимптотично ефективною). Знайдемо вираження для асимптотичної ефективності оцінки
— асимптотична ефективна оцінка (очевидно, що ефективна оцінка буде й асимптотично ефективною). Знайдемо вираження для асимптотичної ефективності оцінки
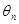
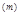 . Тому що при великих п оцінку
. Тому що при великих п оцінку 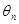
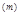 можна вважати незміщеною, то з урахуванням формул (3.11,3.10,3.7) одержимо
можна вважати незміщеною, то з урахуванням формул (3.11,3.10,3.7) одержимо
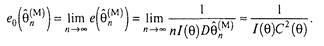
Приклад 3.1.3 Переконаємося в тому, що знайдена методом моментів по випадковій вибірці з генеральної сукупності X ~ N (а, а) оцінка X параметра а є ефективної в класі не зміщених оцінок, а оцінка 
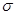
 2 параметра
2 параметра 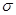 2 є, після виключення зміщення, асимптотично ефективною.
2 є, після виключення зміщення, асимптотично ефективною.
Оцінка X - незміщена, і DX = 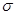 2 /п. Припустивши, що
2 /п. Припустивши, що 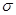 2 відома, і використовуючи формулу (3.10), у якій, з обліком нормальності розподілу,
2 відома, і використовуючи формулу (3.10), у якій, з обліком нормальності розподілу,
1(а) = М(dln f 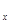 (x,a)/da)
(x,a)/da) 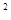 = 1/
= 1/ 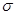 2 одержимо, що е(
2 одержимо, що е(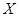 ) = 1. Звідси X - ефективна оцінка.
) = 1. Звідси X - ефективна оцінка.
Оцінка 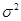 - зміщена; виключивши зміщення, одержимо оцінку
- зміщена; виключивши зміщення, одержимо оцінку
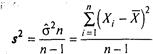

дисперсія котрої Ds 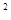 =2
=2 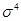 /n-1.
/n-1.
Припустивши, що а відомо, і використовуючи вираження (3.10), у котрому, с обліком нормальності розподілу,
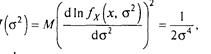
одержимо, що ефективність е(s2) =(n – 1/n)<1, а асимптотична эффективність e0(s2) = lim 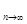 e(s2) = 1. Отже, s2 – асимптотична эффективна оцінка.
e(s2) = 1. Отже, s2 – асимптотична эффективна оцінка.
Зауваження.
Незміщеною і ефективною оцінкою дисперсії є використовувана при відомому значенні параметра а оцінка s 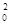 =
= 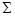
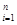 (Xі -a)
(Xі -a) 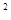 / п, тому що Мs
/ п, тому що Мs 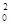 =
= 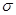 2, Ds
2, Ds 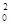 = 2
= 2 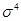 /n и е(s
/n и е(s 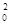 ) = 1.
) = 1.
При виконанні досить загальних умов усі три оцінки: 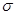 2,s2 і s
2,s2 і s 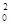
 забеспечені.
забеспечені.
У приведеному прикладі оцінки методу моментів X і 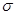 2 є відповідно ефективної й асимптотично ефективної. Однак подібні приклади швидке виключення: набагато частіше оцінки методу моментів із погляду ефективності не є найкращими з можливих навіть при великих п. Р. Фишер показав, що асимптотична ефективність цих оцінок часто значно менше одиниці. Асимптотично ефективні оцінки можуть бути отримані методом максимальної правдоподібності.
2 є відповідно ефективної й асимптотично ефективної. Однак подібні приклади швидке виключення: набагато частіше оцінки методу моментів із погляду ефективності не є найкращими з можливих навіть при великих п. Р. Фишер показав, що асимптотична ефективність цих оцінок часто значно менше одиниці. Асимптотично ефективні оцінки можуть бути отримані методом максимальної правдоподібності.
 2020-01-14
2020-01-14 161
161








