Метод максимальної правдоподібності

В основі методу максимальної правдоподібності лежить поняття функції правдоподібності. Нехай Х= (Х , Х₂,..., Х_п) — випадкова, а х = (х ,х 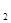,..., х_п) — конкретна вибірки з генеральної сукупності X. Нагадаємо, випадкової називають вибірку, що задовольняє наступним умовам:

випадкові розміри Х , Х₂,,.., Х_п незалежні, тобто

 

                 (3.12)

 

     (3.13)

розподіл кожною з розмірів Х   збігається з розподілом розміру X, тобто при і= 1, 2,..., n.

 

                  (3.14)

Функція правдоподібності — це функція L (х, 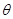), значення якої в точці х визначається співвідношенням:

 

 

З визначення випливає: чим ймовірніше при фіксованому 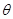 набір х, тим більше значення функції правдоподібності L (x, 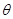), звідси і її назва.

Отже,

 

        (3.15)

 

Відповідно до методу максимальної правдоподібності оцінка максимальної правдоподібності  ^(п) = ( ^п), ,..., ) параметра  = (, ,..., ), при заданому наборі х визначається з умови:

 

                             (3.16)

 

де { } - область припустимих значень для .

Природність такого підходу до визначення оцінки  випливає зі змісту функції L: при фіксованому  функція L (х, 0) — міра правдоподібності набору х; тому, змінюючи , можна простежити, при яких його значеннях набір є більш правдоподібним, а при яких - менше, і вибрати таке значення , при якому наявний набір х буде найбільш правдоподібним.

У ряді випадків   зручніше визначати з умови:

 

In £(х, ) =  In L(x, )                         (3.17)

 

ідентичного умові (3.16): якщо замість функції L узяти In L, крапка максимуму не зміниться. Функцію In L (х, 0) називають логарифмічною функцією правдоподібності.

Відповідно до формули (3.17), для знаходження ^(П) випливає: знайти вирішення системи рівнянь максимальної правдоподібності

 

                                (3.18)

 

при цьому вирішенням вважається лише такий набір * = ( *, *,..., *), що задовольняє (3.18), у якому кожне * дійсно залежить від х;

серед вирішень, що лежать усередині області { }, виділити крапки максимуму;

якщо система (3.18) не визначена, не розв'язна або якщо серед її вирішень немає крапки максимуму усередині { }, то крапку максимуму варто шукати на границі області { }.

Приклад 3.2.1 Знайдемо методом максимальної правдоподібності оцінки параметрів а і b = σ ² нормального розподілу.

Відповідно до формули (3.15), функція правдоподібності

 

логарифмічна функція правдоподібності

 

 

Приватні похідні:

 

 

 

 

Перевіримо достатні умови максимуму функції In L у точці (а*, b* ).

Знайдемо:

 

тому що ∆ >0, А<0, то крапка (а * = ,b *=  ] є крапкою максимуму функції In L. Тому оцінки максимальної правдоподібності =х, = . Оцінки збіглися з оцінками методу моментів.

Приклад 3.2.2 Знайдемо методом максимальної правдоподібності оцінки параметрів а і bрівномірного на відрізку [а,b] розподіли. Відповідно до формули (3.15), функція правдоподібності

 

 

При першій умові система (3.18) не розв'язна, при другому - не визначена. Оцінки  і  варто шукати на границі області припустимих значень для а і b:

 

 

де а . Тоді умова (3.16) прийме вид:

 

 

Тому що функція L(a,b) =1/(b - а)" убуває при зростанні bи убуванні а, то її максимум на області { } досягається в точці .

Приклад 3.2.4 Випадковий розмір Х- число успіхів в одиничному випробуванні: Р(Х = х) = р^х(1 – р) ^1-х, х = 0,1; р - імовірність успіху в одиничному випробуванні. Знайдемо оцінку максимальної правдоподібності   розташовуючи вибіркою х₁, х₂..., х_п, де х _і - число успіхів у і -м випробуванні.

 

де т - число успіхів у л випробуваннях Бернуллі (таку ж оцінку можна одержати і методом моментів). Ця оцінка заможна, незміщена і, у чому неважко переконатися, ефективна.

Відзначена вище природність визначення оцінок максимальної правдоподібності з умови (3.16) підкріплюється їхніми гарними властивостями. Якщо функція щільності fx (х, 9) (функція імовірності Р(Х = х, 9), якщо-дискретна) задовольняє досить загальним умовам регулярності, оцінка максимальної правдоподібності  має при великих я розподіл, близький до нормального з математичним чеканням, рівним , і дисперсією, рівної 1/[ пІ ()], де І() визначається співвідношенням (3.9), є заможної, асимптично несумісної і асимптично ефективної; більш того, якщо існує ефективна оцінка параметра, вона буде єдиним вирішенням рівняння максимальної правдоподібності.

Крім описаних методів оцінювання параметрів існує ряд інших, наприклад метод найменших квадратів, відповідно до котрого

оцінка  параметра  знаходиться з умови:

 

                                (3.19)

 

Звернемо увагу на те, що математичного чекання нормального розподілу з відомим значенням дисперсії умова (3.19) ідентично умові методу максимальної правдоподібності (3.16).

В останні роки розвиваються так називані робастні, або стійкі, методи оцінювання, що дозволяють знаходити оцінки, хоча і є не найкращими в рамках передбачуваного закону розподілу, але має досить стійкі властивості при відхиленні реального закону від передбачуваного.