2020-01-14
172
Сущность метода экстраполяции, т.е. предсказания, заключается в получении упрежденных значений параметра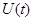 
на основе предшествующих данных. Если текущее значение параметра отличается от предшествующего не больше, чем на величину заданного допуска, то оно отбрасывается. Для предсказания (
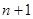)-го отсчета, если известны 
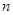предыдущих отсчетов используется формула:
. 
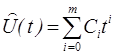(7)
В зависимости от степени полинома различают предсказатели нулевого, первого и т.д. порядка. Рассмотрим предсказатель нулевого порядка (рисунок 7). В этом случае степень полинома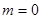 
, а предсказанное значение 
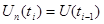. Таким образом, если имеется отсчет 
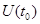, то предполагается, что последующие отсчеты 
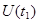и т.д. равны .
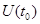Относительно величины отсчета 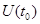устанавливается зона 
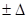. Эта зона называется зоной сравнения или апертурой. Для каждого 
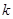-го отсчета, следующего за 
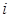-ым существенным отсчетом, вычисляется разность:
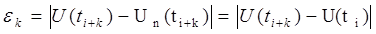. (8)
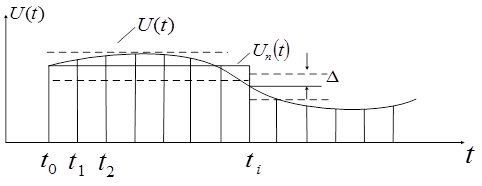
Рисунок 7
Отсчет считается существенным, если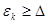 
.
Сжатие с помощью полинома нулевого порядка требует запоминание последнего существенного отсчета.
|
|
|
Блок - схема алгоритма данного метода показана на рисунке 8.
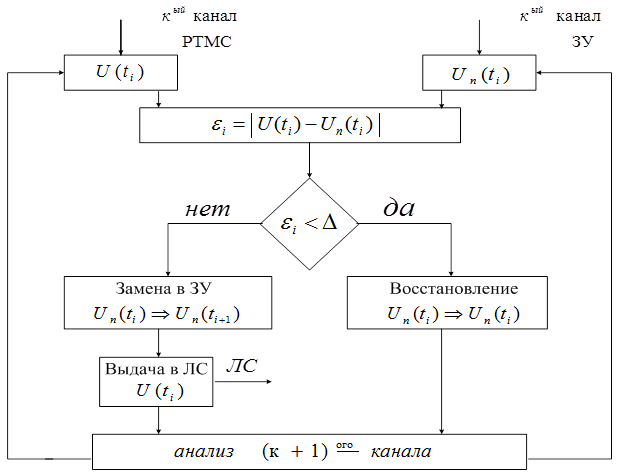
Рисунок 8
Рассмотрим теперь предсказатель первого порядка. Степень полинома в этом случае m=1. Для построения полинома требуется два предшествующих отсчета, через которые проводится прямая линия. Предсказанное значение для последующих отсчетов лежит на этой линии (рисунок 9).
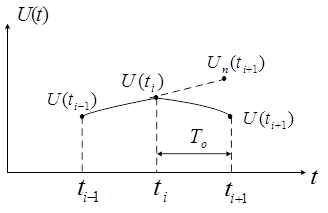
Рисунок 9
Предсказанное для момента времени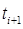 
значение параметра рассчитывается по формуле:
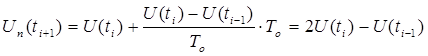. (9)
Если ошибка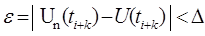 
, то отсчет исключается. В этом случае для расчета предсказанного значения в точке 
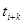используется формула:
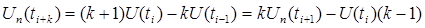. (10)
Сжатие с помощью предсказателя первого порядка требует запоминание последнего существенного отсчета и предсказанного значения отсчета (рисунок 10).
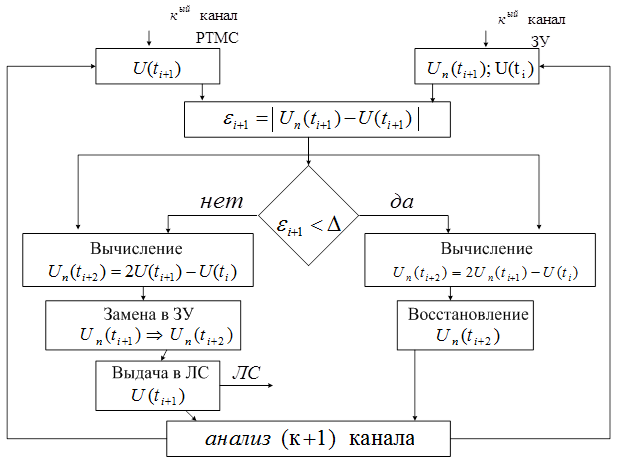
Рисунок 10
Согласно экспериментальным данным при сжатии медленно меняющихся параметров предсказатель нулевого порядка дает коэффициент сжатия около 50, а предсказатель первого порядка – 70. Использование полиномов более высокого порядка даёт небольшое приращение коэффициента сжатие, но приводит к увеличению вычислений и усложнению экстраполятора. Наиболее помехоустойчивы экстраполяторы низких порядков, поэтому обычно используются экстраполяторы нулевого и первого порядка.
