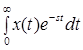Преобразование Лапласа

Системная функция T(s) в общем случае является функцией комплексного переменного [2]. Поэтому для исследования системных функций используется алгебра комплексных чисел, где  .

По определению системная функция есть отношение выходной величины к входной величине. Поэтому, если известно возмущение на входе вида и системная функция T(s), то выходная величина будет равна

.

При анализе системных функций как функций комплексной переменной очень удобно пользоваться односторонним преобразованием Лапласа. Одностороннее преобразование Лапласа представляет собой оператор, отображающий функцию времени в функцию комплексной переменной  в соответствии с формулой:

	X(s) = L [ x(t) ] =

Данный интеграл отображает функцию x(t) в функцию переменной s, причем нас интересуют значения X(s) не в одной точке, а в некоторой области комплексной s –плоскости. Поскольку при задании X(s) в некоторой области s –плоскости можно однозначно восстановить x(t) для t>0, преобразование Лапласа обеспечивает взаимно однозначное соответствие. Именно это свойство взаимной однозначности обуславливает полезность преобразование Лапласа. Предположим нам необходимо описать оператор , характеризующий некоторую систему. Вместо прямого

решения этой задачи проще и нагляднее описывать оператор , связывающий преобразования Лапласа для входного и выходного сигналов. В силу взаимной однозначности это эквивалентно искомому описанию. S- называется комплексной частотой, а оператор  характеризует систему в частотной области, тогда как  характеризует ее во временной области.

Преобразование Лапласа в качестве математического инструмента для вычисления отклика на конкретные воздействия полезно главным образом для сосредоточенных линейных инвариантных [ЛИВ] во времени цепей. В случае нелинейных или изменяемых во времени систем описание или оценка F[s] обычно ничуть не легче, чем f[t]. Для простейших ЛИВ систем с простыми входными воздействиями наиболее эффективны прямые методы. Очень большие системы во всех случаях требуют технических вспомогательных средств. Методы преобразования Лапласа сопряжены с обработкой матриц, содержащих алгебраические элементы (функции s), и включают нахождение корней полиномов высокого порядка. Однако внутри своей области преобразование Лапласа является эффективным средством для решения задач теории цепей.