Заданный ток в элементе электрической цепи может рассматриваться как некоторое возмущение. Ответом на это возмущение (реакция) будет напряжение на зажимах элемента. Для большей общности анализа электрических цепей желательно найти такой вид возмущения, который объединял бы все или большинство видов возмущений. Этому свойству отвечает экспоненциальное возмущение:
 или
или 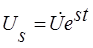
где  и
и  - обобщенные комплексные амплитуды, а s – комплексная частота. При таком воздействии на линейные цепи значения токов и напряжений на любых участках представляют собой тоже экспоненциальные функции. При этом соотношения между амплитудами токов и напряжений подчиняются закону Ома и законам Кирхгофа аналогично соотношениям в цепи постоянного тока. Основное отличие от цепей постоянного тока заключается в том, что при экспоненциальном воздействии, кроме омического сопротивления, необходимо учитывать индуктивные и емкостные сопротивления, а также сопротивления взаимной индукции. Величины этих сопротивлений зависят от показателя степени
- обобщенные комплексные амплитуды, а s – комплексная частота. При таком воздействии на линейные цепи значения токов и напряжений на любых участках представляют собой тоже экспоненциальные функции. При этом соотношения между амплитудами токов и напряжений подчиняются закону Ома и законам Кирхгофа аналогично соотношениям в цепи постоянного тока. Основное отличие от цепей постоянного тока заключается в том, что при экспоненциальном воздействии, кроме омического сопротивления, необходимо учитывать индуктивные и емкостные сопротивления, а также сопротивления взаимной индукции. Величины этих сопротивлений зависят от показателя степени  и определяются соотношениями:
и определяются соотношениями:
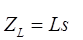 для индуктивности и
для индуктивности и  для емкости.
для емкости.
Математические методы анализа цепей и переходных процессов в них
Системная функция
Для анализа электрических цепей очень удобно использовать понятие контурных токов [1]. Написав для каждого контура свое уравнение, мы получаем некую матрицу уравнений. Решение этой матрицы обычно приводит к нахождению токов в каждом контуре цепи. Точно такую операцию можно произвести и для узловых напряжений.
В случае, если цепь пассивна и имеется один вход, к зажимам которого подключается внешний источник напряжения 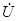 , контурные токи определяются из системы уравнений:
, контурные токи определяются из системы уравнений:
 ,
,
 ,
,
………..
 ,
,
где 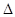 - определитель матрицы контурных сопротивлений;
- определитель матрицы контурных сопротивлений;
 - алгебраическое дополнение элемента 1k этого определителя.
- алгебраическое дополнение элемента 1k этого определителя.
Анализируя зависимость, например, контурного тока в контуре lm от входного напряжения 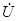 получаем функцию:
получаем функцию:
 ,
,
что является системной функцией проводимости, а отношение напряжения в ветви lm к напряжению на входе 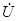

представляет собой системную передаточную функцию напряжения от ветви 1 к ветви lm.
Определяя таким образом системные функции для всех ветвей, можно, очевидно, рассмотреть множество этих функций. Все они обладают следующей особенностью:
так как 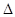 и
и  - соответственно полиномы от контурных сопротивлений Z, а сопротивление Z в свою очередь является полиномом s, то любая системная функция должна иметь вид рациональной дроби переменной s:
- соответственно полиномы от контурных сопротивлений Z, а сопротивление Z в свою очередь является полиномом s, то любая системная функция должна иметь вид рациональной дроби переменной s:
 ,
,
где P(s) и Q(s) – полиномы.
Если найти корни полиномов P(s) и Q(s) путем решения уравнений:
 (корни: s1 , s1 ,…. sm)
(корни: s1 , s1 ,…. sm)
и
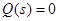 (корни: sa, sb,…. sn),
(корни: sa, sb,…. sn),
то системную функцию можно представить в виде:
 .
.
Корни s1 , s2 ,…. sm называются нулями системной функции, а корни sa, sb,…. sn – полюсами системной функции. При равенстве s одному из нулей s1 , s2 ,…. sm системная функция обращается в ноль, а равенстве одному из полюсов sa, sb,…. sn – в бесконечность.
 2020-01-14
2020-01-14 146
146








