Понятие о площади. Свойства площади

Обычно говорят, что площадь  фигуры  есть число, показывающее, из скольких единиц площади составляется фигура. Однако это не определение, а только описание того, что такое площадь. Легко понять, что прямоугольник со сторонами 3 и 5 см «составляется» из 15 квадратных сантиметров (его легко разрезать на 15 квадратов со стороной 1 см; рис. 1.3,а)

 

Рис. 1.3,а

 

 

Но сколько подобных квадратов нужно, чтобы «составить» круг радиуса 2 см (рис. 1.3, б), совершенно неясно.

 

Рис.1.3,б

 

Строгое математическое определение площади можно получить с помощью палетки – прозрачной пластинки с нанесенной на нее сеткой из равных квадратов. Представим, что такая палетка лежит на плоскости. Иначе говоря, плоскость разбита на квадраты со стороной, равной 1. Если фигура  полностью помещается в фигуре, составленной, например, из81 квадрата палетки, и содержит фигуру из 43 квадратов (рис. 1.4), то .

 

Рис. 1.4

 

Для большей точности измерения можно каждый квадрат палетки разбить на сто квадратов (стороны которых в 10 раз меньше, чем у квадратов первой палетки, а площадь равна 1/100). Новая, более мелкая палетка даст и более тесные границы, в которых заключена площадь фигуры , скажем, . Если каждый квадрат второй палетки снова разбить на 100 квадратов, точность измерения ещё увеличится – например, получатся границы . Так, используя набор палеток со всё более мелкой сеткой, мы будем приближаться к пределу – площади  фигуры .

Но здесь есть одна тонкость. Вначале мы получили отрезок , где 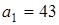, , в котором содержится искомое число . Затем этот отрезок уменьшили до , где 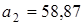, . Потом уменьшили ещё – до 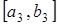, где , , и т. д. Но пересечение системы вложенных отрезков

числовой прямой есть либо одна точка (в том случае, когда имеется только одно число , принадлежащее все рассматриваемым отрезкам (рис. 1.5), фигуру  называют квадрируемой (по Жордану), а число  - площадью фигуры .

 

Рис. 1.5

 

Второй случай, когда пересечение всех отрезков представляет собой отрезок, а не одну точку, на первый взгляд кажется просто невозможным. Ведь всякая фигура имеет какую-нибудь площадь S (F). Число S (F) и должно быть единственной общей точкой рассматриваемых отрезков. Но на самом деле это не так. Следующий пример подтверждает это.

Возьмём квадрат Q ₁ со стороной 1. Выбросим из него крестообразную фигуру площадью , как показано на рис. 1.6.

 

рис. 1.6

 

Остаётся фигура Q ₂ из четырёх равных квадратов, примыкающих к вершинам Q ₁. (Сторона каждого из них составляет ). Теперь в каждом из квадратов фигуры Q ₂ вновь построим, а затем удалим крестообразную фигуру. Её размер определим из условия, что сумма площадей четырёх таких фигур была равна  .  Получим фигуру Q ₃ из 16 квадратов. Из каждого из них опять выбросим крестообразную фигуру так, чтобы сумма площадей всех 16 таких «крестов» была равна 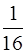. Получим фигуру Q ₄ из 64 квадратов и т. д.

Обозначим через F пересечение всех фигур Q ₁, Q ₂, Q ₃, Q ₄, … Другими словами, F получается, если из квадрата Q ₁ выбросить по очереди все «кресты». Общая площадь фигур, выбрасываемых из Q ₁, равна 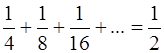. Значит, на долю множества F остаётся площадь . Это кажется невероятным: ясно, что в фигуре F нет ни одного, пусть самого маленького, целого квадратика, и тем не менее она имеет площадь, равную .

Попробуем теперь измерить площадь фигуры F по Жордану (т. е. с помощью палеток). Какую бы мелкую палетку мы не взяли, площадь фигуры, составленной из квадратов палетки и включающей в себя F, равна нулю (поскольку в F нет ни одного целого квадрата. Таким образом, каждый из получающихся отрезков

 

 

(а потому и пересечение всех этих отрезков) содержит отрезок , т. е. их пересечение не состоит из одной точки. Значит, фигура F неквадрируема.

Способ измерения площадей с помощью палеток был предложен в XIX веке французским математиком Камилем Жорданом. Другой французский математик – Анри Лебег предложил более общее определение площади. Построенная выше фигура F неквадрируема по Жордану, но имеет площадь (равную ), по определению Лебега, или, как говорят, измерима по Лебегу. Если же фигура квадрируема по Жордану, то она обязательно измерима и по Лебегу (и имеет ту же площадь).

А какие плоские фигуры квадрируемы? Прежде всего многоугольники. Для других фигур применяют следующую теорему:

Плоская фигура F (рис. 1.7) в том и только в том случае квадрируема, если для любого положительного числа  найдутся два таких многоугольника M и N, что М содержится в F, а N содержит F, и при этом

 

.

 

Рис 1.7

 

Другими словами, квадрируемы фигуры, которые можно сколь угодно точно приблизить многоугольниками. Например, площадь круга находят как предел площади вписанного в него или описанного около него правильного n-угольника при .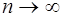

Поскольку обе площади имеют общий предел, их разность стремится к нулю, значит, круг – квадрируемая фигура. Вообще, любая плоская выпуклая фигура квадрируема. Квадрируема и криволинейная трапеция под графиком непрерывной функции , заданной на отрезке .

Кроме приведённого выше определения площади с помощью палеток имеется ещё одно, аксиоматическое определение. Прежде чем его сформулировать рассмотрим некоторые свойства площади (будем иметь в виду только площадь по Жордану).

Обозначим через Q множество всех квадрируемых плоских фигур, тогда площадь S (F) есть числовая функция, определённая на данном множестве. Перечислим свойства, которыми она обладает.

А. Неотрицательность. Площадь любой квадрируемой фигуры F неотрицательна: . Не исключается нулевое значение площади, поскольку, например, любой отрезок представляет собой квадрируемую фигуру нулевой площади.

В. Аддитивность. Пусть F ₁ и F ₂ – две квадрируемые фигуры, у которых нет общих внутренних точек. Обозначим через F объединение этих фигур. Тогда фигура F  квадрируема и справедливо равенство . То же имеет место при объединении не двух, а большего числа фигур, попарно не имеющих общих внутренних точек.

С. Инвариантность. Если две квадрируемые фигуры F ₁ и F ₂ равны, т. е. одна получается из другой с помощью движения, то площади таких фигур равны: . Иначе говоря, площадь не изменяется при движениях.

D. Нормируемость. При определении площади фигуры задаётся некоторая единица площади – квадрат К, сторона которого равна динице длины: .

Очевидно, что площадь , определяемая с помощью палеток, действительно удовлетворяет свойствам А и D. Проверить два других свойства сложнее. Например, если фигура F ₁ переходит в F ₂ при повороте, то эти две фигуры будут по-разному расположены относительно палеток и доказательство равенства их площадей (свойство С) требует некоторых усилий. Тем не менее можно утверждать:

На множестве Q всех квадрируемых фигур существует одна и только одна функция, которая обладает свойствами A, B, C, D.

То есть всякая функция на множестве Q, удовлетворяющая всем четырём свойствам, совпадает с .

Стало быть, свойства A, B, C, D можно принять за аксиомы площади, т. е. определить площадь как функцию на множестве квадрируемых фигур Q, удовлетворяющую данным аксиомам. Это и есть аксиоматическое определение площади. Все остальные её свойства можно вывести из перечисленных аксиом. Например, формулы для вычисления площадей многоугольников вытекают именно из аксиом A, B, C, D точно так же, как формулы площади круга, эллипса и других фигур.

Заметим, что и в геометрии Лобачевского, и в сферической геометрии площадь определяется теми же аксиомами. Однако палетками пользоваться уже не приходится; за эталон площади принимают не квадрат, а иную фигуру – квадратов на плоскости Лобачевского и сфере просто нет. Интересно, что в обеих геометриях площадь многоугольника пропорциональна разности между суммой его углов и суммой углов плоского многоугольника с тем же числом сторон.