Урок 1
Тема: «Решение задач с использованием свойств площадей»
Цель: Освоение различных путей поиска решения задач с использованием свойств площадей.
Оборудование: Таблица «Свойства площадей».

С – 1 С – 2

С – 3 С – 4
С – 5 С – 6

С - 7 С – 8
Рис. 2.1
Ход урока
Сегодня мы на уроке будем решать задачи с использованием свойств площадей.
Двух учеников приглашают к доске.
I. Запишите на доске все формулы площади треугольника.
II. Запишите на доске формулы площади трапеции.
Ответы
I. 1).  2)
2) 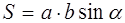 3)
3)  ,
где ,
где  4)
4)  5)
5)  ,
r – радиус вписанной в треугольник окружности
6) ,
r – радиус вписанной в треугольник окружности
6) 
| II. 1).  2)
2)  , где MN – средняя линия трапеции
3) , где MN – средняя линия трапеции
3)  ,
где d 1, d 2 – диагонали трапеции, α – угол между ними
4) ,
где d 1, d 2 – диагонали трапеции, α – угол между ними
4)  ,
где с – боковая сторона трапеции, h –перпендикуляр из середины другой боковой стороны на первую или её продолжение ,
где с – боковая сторона трапеции, h –перпендикуляр из середины другой боковой стороны на первую или её продолжение
|
Пока ученики записывают формулы, спросить учеников с мест правила «Свойства площадей».
Ответ
1). Каждая фигура имеет положительную площадь.
2). Площадь квадрата со стороной равной единице длины равна единице площади.
3). Если фигура разбивается на две части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.
Рассмотрите площади треугольника, написанные на доске.
Вопрос. Какая из формул является основной?
Ответ.  .
.
Назовите следствия из этой формулы, используя таблицу «Свойства площадей».
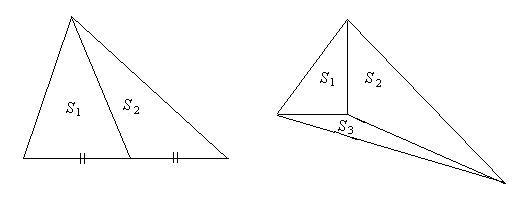
С–1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не изменится.
С–2. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).
С–3. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.
С–4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
С–5. Медиана треугольника делит его на 2 равновеликие части.
С–6. Медианы треугольника делят его на три равновеликие части.
С–7. Медианы треугольника делят его на 6 равновеликих частей.
С–8. Средняя линия треугольника площади  отсекает от него треугольник площади
отсекает от него треугольник площади  .
.
Решение задач
Задача 1. Дано  - трапеция,
- трапеция,  и
и  - диагонали. Пересекающиеся диагонали разбивают трапецию на 4 треугольника с вершиной в точке О.
- диагонали. Пересекающиеся диагонали разбивают трапецию на 4 треугольника с вершиной в точке О. 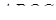 и
и 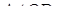 - треугольники, которые прилегают к основаниям и треугольники
- треугольники, которые прилегают к основаниям и треугольники  и
и  - треугольники, которые прилегают к боковым сторонам. Обозначим
- треугольники, которые прилегают к боковым сторонам. Обозначим  ,
,  ,
,  ,
,  ,
,  .
.
Найдите связь между площадями треугольника.

Рис. 2.2
Выразите площадь трапеции через  и
и 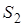 , т. е. через площади треугольников, прилегающих к основаниям трапеции.
, т. е. через площади треугольников, прилегающих к основаниям трапеции.
Так как  , то надо выразить
, то надо выразить  и
и  через
через  и
и 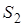 .
.
Вопрос. Что можно сказать про площади  и
и  ?
?
Ответ.  =
=  , т. к. треугольники
, т. к. треугольники  и
и  имеют одинаковые площади, а если от равных отнять площадь
имеют одинаковые площади, а если от равных отнять площадь  , то получим равные площади
, то получим равные площади  и
и  .
.
Выразите  через
через  и
и 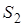 .
. 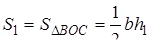 ,
,  .
.
Докажите, что  и
и 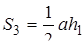 .
.

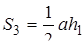 (2.1)
(2.1)

 (2.2)
(2.2)
Перемножив (2.1) и (2.2), получим
 .
.
 .
.
Вопрос. Как сформулировать правило, которое мы вывели?
Ответ. Площадь треугольника, прилегающего к боковой стороне трапеции есть среднее геометрическое между площадями треугольников, прилегающих к основаниям трапеции.
Вопрос. Как вывести соотношение  , используя свойства площадей?
, используя свойства площадей?
Ответ.  .
.
Вопрос. Какое свойство площадей здесь использовались?
Ответ. С – 3, С – 2 (ученики отвечают устно).
Вопрос. Как можно ещё вывести соотношения  ?
?
Ответ.  .
.

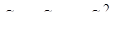 ;
;  .
.
Найдите площадь трапеции (рис. 2.3)

Рис. 2.3

 или
или  .
.
Таким соотношением связана площадь трапеции с площадями треугольников, прилегающих к её основаниям. Итак, для трапеции
 .
.
Вопрос. Справедливо ли это соотношение для любого четырёхугольника?
Ответ. Нет, т. к.  .
.
Основания у треугольников  и
и  одинаковые (рис. 2.4), но их вершины не на параллельных прямых.
одинаковые (рис. 2.4), но их вершины не на параллельных прямых.

Рис. 2.4
Вопрос. А какое соотношение между  можно вывести для четырёхугольника (рис. 2.4)?
можно вывести для четырёхугольника (рис. 2.4)?
Ответ.  ,
,
т. е. произведения площадей треугольников, прилегающих к противоположным сторонам четырёхугольника равны.
Задача 2. (обратная).
Дано: выпуклый четырёхугольник 
Докажите, что этот четырёхугольник есть трапеция.
Доказательство.
 С другой стороны,
С другой стороны,  (рис. 2.4).
(рис. 2.4).  , следовательно
, следовательно  , но
, но  , (рис. 2.4), следовательно
, (рис. 2.4), следовательно  , следовательно
, следовательно  , следовательно
, следовательно 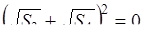 , следовательно
, следовательно  и
и  , т. е.
, т. е.  , а это означает, что
, а это означает, что  , т. е. четырёхугольник
, т. е. четырёхугольник  - трапеция.
- трапеция.
Задача 3. Через некоторую точку, взятую внутри треугольника проведены 3 прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют треугольник на 6 частей, из которых три треугольника с площадями 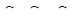 . Найдите площадь треугольника.
. Найдите площадь треугольника.

Рис. 2.5
Дано:  .
.  .
.  .
.  .
.  ,
,  ,
,  .
.
Найдите  .
.
Решение.
1)  ~
~ 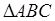 , следовательно
, следовательно  9площади подобных треугольников относятся как квадрат коэффициента подобия).
9площади подобных треугольников относятся как квадрат коэффициента подобия).
2)  ;
; 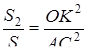 ;
;  ;
;  .
.
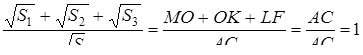 .
.
 , отсюда
, отсюда  .
.
Итог урока
Повесить таблицу «Итог урока» (сделать из достаточно плотной бумаги, с магнитами на обратной стороне, прикрепляется мгновенно на обратную доску).
Вопрос. Мысленно вернитесь ко всем задачам, которые были рассмотрены на уроке. Попытайтесь вспомнить из всех свойств площадей, какие свойства мы применяли на уроке.
Ответ. 1) Равные фигуры имеют одинаковые площади.
2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.
3) Если от равных отнять равные, то получим равные.
Вопрос. Какие следствия из формулы  мы применяли?
мы применяли?
Ответ. С – 1, С – 2, С – 3, С – 4, С – 5 все следствия ученики рассказывают.
Вопрос. Из множества формул для нахождения площади простых фигур какие бы вы использовали?
Ответ.  ;
;  ;
;  ;
;  .
.
Задание на дом
1. Диагонали делят трапецию на 4 треугольника. Площади двух из них равны 1 см2 и 2 см2. Какой может быть площадь трапеции?
2. Точки  - середины сторон выпуклых четырёхугольников
- середины сторон выпуклых четырёхугольников  и
и 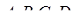 . Докажите, что
. Докажите, что  .
.
3. Дано: 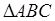 ;
;  - середины сторон
- середины сторон  соответственно.
соответственно.  пересекает
пересекает  в точке
в точке  . Докажите, что
. Докажите, что  (задача автора).
(задача автора).
4. В параллелограмме  точки
точки 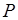 и
и  делят диагональ
делят диагональ  на три равные части. Точки
на три равные части. Точки  и
и  - середины сторон
- середины сторон  и
и  . Найдите отношение площади четырёхугольника
. Найдите отношение площади четырёхугольника  к площади параллелограмма
к площади параллелограмма  (задача автора).
(задача автора).
5. На одной стороне угла с вершиной  отложены равные отрезки
отложены равные отрезки  ,
,  и
и  . На другой стороне – равные отрезки
. На другой стороне – равные отрезки 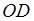 ,
, 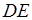 и
и  . Докажите, что
. Докажите, что  и
и  равновелики.
равновелики.
Домашнее задание выдаётся каждому ученику на листке.
Урок 2
 2020-01-14
2020-01-14 179
179








