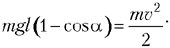2020-01-14
88
Решения заданий С 1– С 5 части 3 (с развёрнутым ответом) оцениваются экспертной комиссией. На основе критериев, представленных в приведённых ниже таблицах, за выполнение каждого задания в зависимости от полноты и правильности данного учащимся ответа выставляется от 0 до 4 баллов.
C 1. Образец возможного решения
| Элементы ответа: 1. Указано, что в опыте наблюдается явление интерференции света. Приведено объяснение образования интерференционного максимума: максимум образуется в тех местах плёнки, где разность хода волны, отражённой от двух поверхностей плёнки, и волны, прошедшей плёнку без отражений, достигает чётного числа полуволн. (Либо это объяснение приведено в виде рисунка и соответствующей формулы.) 2. Указано, что толщина плёнки увеличивается книзу. Поэтому условие интерференционного максимума в нижней части цветных полос будет выполняться для видимого света с максимальной длиной волны, т.е. красного. | |
| Критерии оценки выполнения задания | Баллы |
| Приведены оба элемента правильного ответа | 2 |
| Приведены оба элемента правильного ответа, но допущено не более одной ошибки, ИЛИ приведён только один элемент правильного ответа | 1 |
| Приведён только один элемент правильного ответа, но в нём допущена ошибка | 0 |
| Максимальный балл | 2 |
C 2. Образец возможного решения
| На основании второго закона Ньютона ускорение, вызванное суммой действующих на груз сил тяжести и натяжения нити, при прохождении положения равновесия равно центростремительному ускорению: По закону сохранения механической энергии, для груза маятника (за начало отсчёта потенциальной энергии выбрано нижнее положение груза):
Ответ в общем виде и в численной форме:
| |
| Критерии оценки выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: 1) верно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом (в данном решении – второй закон Ньютона, формула для центростремительного ускорения, закон сохранения механической энергии); 2) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу, и представлен ответ. При этом допускается решение «по частям» (с промежуточными вычислениями). | 3 |
| – Представлено правильное решение только в общем виде, без какихлибо числовых расчётов. ИЛИ – Правильно записаны необходимые формулы, записан правильный ответ, но не представлены преобразования, приводящие к ответу. ИЛИ – В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу. | 2 |
| – В решении содержится ошибка в необходимых математических преобразованиях и отсутствуют какиелибо числовые расчёты. ИЛИ – Записаны и использованы не все исходные формулы, необходимые для решения задачи, или в ОДНОЙ из них допущена ошибка. | 1 |
| Все случаи решения, которые не соответствуют указанным выше критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т.п.). | 0 |
C 3. Образец возможного решения
Внутренняя энергия одноатомного идеального газа пропорциональна его температуре и числу молей газа: U = (3/2) 
RT. Запишем уравнение Клапейрона–Менделеева: pV = RT (p – давление газа, V – объём сосуда, R – газовая постоянная, T – температура газа, – число молей газа). Из него видно, что произведение T пропорционально произведению pV. Значит, согласно условию задачи, внутренняя энергия газа (как и произведение pV) уменьшилась в 6 раз.
Ответ. U уменьшилась в 6 раз.
C 4. Образец возможного решения
Количество теплоты, согласно закону Джоуля–Ленца:
Q = (U 2/ R) • t. (1)
Это количество теплоты затратится на нагревание проводника:
Q = cm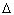 
T, (2)
где масса проводника
m =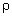 
lS, (3)
S – площадь поперечного сечения проводника.
Сопротивление проводника:
R = (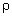 эл l)/ S. (4)
Из (1)–(4), получаем: 
C 5. Образец возможного решения
Ядро атома первоначально покоится, поэтому суммарный импульс продуктов реакции будет равен нулю. По условию задачи, суммарная кинетическая энергия продуктов реакции равна 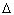Е. Поэтому законы сохранения энергии и импульса для  -распада ядра покоящегося нейтрального атома:
В магнитном поле под действием силы Лоренца ион начинает двигаться по дуге окружности. Уравнение движения тяжёлого иона с зарядом q = –2 e в магнитном поле: 
|
| Решая систему трёх уравнений, получаем:
| |
| Критерии оценки выполнения задания | Баллы |
| Приведено полное правильное решение, включающее следующие элементы: 1) приведены комментарии к использованию законов сохранения энергии и импульса, движения частицы в магнитном поле, верно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом (в данном решении – законы сохранения энергии и импульса, второй закон Ньютона и формулы расчёта центростремительного ускорения и силы Лоренца); 2) проведены необходимые математические преобразования и расчёты, приводящие к правильному ответу, и представлен ответ. | 4 |
| – Представлено правильное решение, но не приведены комментарии к использованию законов. ИЛИ – Представлено правильное решение только в общем виде, без какихлибо числовых расчётов. | 3 |
| – Правильно записаны необходимые формулы, записан правильный ответ, но не представлены комментарии к использованию законов и преобразования, приводящие к ответу. ИЛИ – В математических преобразованиях или вычислениях допущена ошибка, которая привела к неверному ответу, и не представлены комментарии к использованию законов. | 2 |
| – В решении содержится ошибка в необходимых математических преобразованиях, отсутствуют комментарии к использованию законов и какиелибо числовые расчёты. ИЛИ – Записаны и использованы не все исходные формулы, необходимые для решения задачи, или в ОДНОЙ из них допущена ошибка. | 1 |
| Все случаи решения, которые не соответствуют указанным выше критериям выставления оценок в 1, 2, 3 балла (использование неприменимого закона, отсутствие более одного исходного уравнения, разрозненные записи и т.п.). | 0 |
