Теорема 2.3.1. Если  , то
, то  – поле тогда и только тогда, когда Q +(-a2) – поле.
– поле тогда и только тогда, когда Q +(-a2) – поле.
Доказательство. По теореме 2.1.1 Q +(ai) – поле равносильно существованию
f ¹0, f (ai)=0.
Так как все степени aiÎ Q +(ai). Рассмотрим некоторый многочлен
 .
.
Равенство выполняется тогда и только тогда, когда действительная и мнимая часть равны нулю.
То есть,

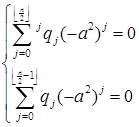
Это верно тогда и только тогда, когда Q +(- a2) – поле.
Получили, что Q +(ai) – поле тогда и только тогда, когда Q +(-a 2) – поле. ■
Как следствие получаем более ценные утверждения.
Следствие 1. Если  , то Q +(ai) – полуполе тогда и только тогда, когда Q +(-a2) – полуполе.
, то Q +(ai) – полуполе тогда и только тогда, когда Q +(-a2) – полуполе.
Следствие 2. Если  и Q +(-b2) – полуполе, aÎ Q +(-b2), то Q +(a + bi) – полуполе.
и Q +(-b2) – полуполе, aÎ Q +(-b2), то Q +(a + bi) – полуполе.
Теорема 2.3.2. Пусть 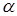 – комплексный корень квадратного трехчлена f(x) неприводимого над Q. Тогда
– комплексный корень квадратного трехчлена f(x) неприводимого над Q. Тогда  – полуполе в том и только том случае, когда f(x) имеет положительный действительный корень.
– полуполе в том и только том случае, когда f(x) имеет положительный действительный корень.
Доказательство. Пусть  удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней. Тогда
удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней. Тогда  , где D – дискриминант минимального соотношения.
, где D – дискриминант минимального соотношения.
Рассмотрим минимальный многочлен, соответствующий данному минимальному значению. Он имеет вид  . Если b, c ≥ 0, то имеем многочлен из
. Если b, c ≥ 0, то имеем многочлен из  . Пусть многочлен имеет два отрицательных корня, тогда
. Пусть многочлен имеет два отрицательных корня, тогда  ,
,  . То есть
. То есть  . Если многочлен не имеет действительных корней,
. Если многочлен не имеет действительных корней,  то
то
 (*)
(*)
То есть,  .
.
Рассмотрим  .
.
При 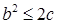 получаем многочлен из Q +[ x ]. Пусть
получаем многочлен из Q +[ x ]. Пусть  . Введем обозначения:
. Введем обозначения:
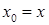 ,
,  ,
,  ,
,

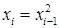 ,
,  ,
,  .
.
Тогда многочлен примет вид  . Умножим его на
. Умножим его на  , получим многочлен
, получим многочлен  . Если
. Если  , то это искомый многочлен иначе умножим его на
, то это искомый многочлен иначе умножим его на  .
.
Докажем, что, проделав такую операцию достаточно большое количество раз, мы получим многочлен из Q +. Докажем, что найдется такие k, что  . При этом
. При этом  . Для начала найдем дискриминант уравнения
. Для начала найдем дискриминант уравнения  .
.

То есть, дискриминант Dl+1 имеет тот же знак, что и Dl. Так как D0 <0, то пользуясь методом математической индукции заключаем, что любой дискриминант Dl <0.
Рассмотрим неравенство  , подставим
, подставим  ,
, 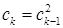 . Получим
. Получим
 .
.
То есть,
 .
.
Зная, что  заметим
заметим
 .
.
Итак, для доказательства нам достаточно установить, что
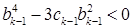 .
.
То есть,
 .
.
Пусть аналогичными рассуждениями мы установили, что нам достаточно доказать неравенство
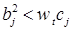 .
.
Тогда
 .
.
Раскрывая скобки и приводя подобные слагаемые, получим, что
 .
.
Используя оценку  и деля на положительный элемент
и деля на положительный элемент  , получаем
, получаем
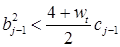 .
.
Обозначим  . Рассмотрим отображение
. Рассмотрим отображение  , заданное по правилу
, заданное по правилу  . При
. При  ,
,  . Отображение является сжимающим. Оно имеет единственную неподвижную точку. Найдем ее:
. Отображение является сжимающим. Оно имеет единственную неподвижную точку. Найдем ее:  . Откуда
. Откуда  . Заметим, что
. Заметим, что 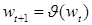 . Последовательность
. Последовательность  стремится к 4. То есть, нам достаточно установить, что
стремится к 4. То есть, нам достаточно установить, что  , а это следует из (*). Итак, мы доказали, что
, а это следует из (*). Итак, мы доказали, что  . То есть, мы нашли такой многочлен,
. То есть, мы нашли такой многочлен,  , что
, что  . Итак, мы доказали, что если
. Итак, мы доказали, что если  удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней, то
удовлетворяет минимальному соотношению, являющемуся квадратным уравнением без положительных корней, то 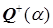 – поле. ■
– поле. ■
Следствие 1. Если 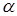 – мнимый корень квадратного трехчлена, то
– мнимый корень квадратного трехчлена, то 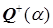 ‑ поле.
‑ поле.
Следствие 2. Любое простое расширение  является полем
является полем  , порожденным минимальным соотношением 2 степени.
, порожденным минимальным соотношением 2 степени.
Доказательство.
Заметим, что  . Покажем, что для любого a Î Q найдется такой квадратный многочлен
. Покажем, что для любого a Î Q найдется такой квадратный многочлен  , что
, что  - его корень многочлена. Для этого достаточно представить
- его корень многочлена. Для этого достаточно представить  . Возьмем такой
. Возьмем такой  , что
, что  , тогда
, тогда 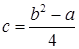 . Очевидно,
. Очевидно,  . Таким образом, нам удалось найти многочлен из
. Таким образом, нам удалось найти многочлен из  . То есть,
. То есть,  - поле. ■
- поле. ■
Рассмотрим последовательность действительных чисел 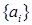 :
:
 (**)
(**)
Будем говорить, что последовательность  задается числами p и q.
задается числами p и q.
Лемма 2.3.3. Существует n, что  .
.
Доказательство. Пусть  . Покажем, что последовательность
. Покажем, что последовательность  убывающая.
убывающая.
 ,
,
то есть  .
.
Пусть  , тогда
, тогда

Так как  ,
,  то
то 
Пользуясь методом математической индукции, заключаем, что  , то есть
, то есть  - убывающая.
- убывающая.
Так как  - монотонно убывающая и ограничена снизу 0, то существует
- монотонно убывающая и ограничена снизу 0, то существует 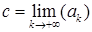 . Тогда
. Тогда  .
.
То есть,  . Но тогда
. Но тогда
 ,
,
 ,
,
что невозможно для 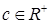 . То есть,
. То есть,  . ■
. ■
Лемма 2.3.4. Если  , то существует
, то существует  , что
, что  .
.
Доказательство. Запишем а и b в виде десятичных дробей:
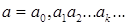 ,
,  Так как
Так как 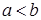 , то существует k, что
, то существует k, что  и
и  .
.
Тогда  . Рассмотрим число
. Рассмотрим число  .
.
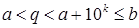
То есть,  . ■
. ■
Теорема 2.3.5. Если 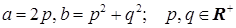 и
и  , то
, то
 .
.
Доказательство. По лемме 2.3.3,  . Пусть
. Пусть  .
.
Если n=1, то  . Рассмотрим
. Рассмотрим  .
.

То есть,
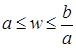 .
.
Так как  . По лемме 2.3.4
. По лемме 2.3.4 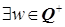 . Тогда
. Тогда
 .
.
Рассмотрим n > 1.
Пусть  .
.
Покажем, что 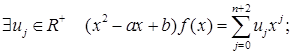
Раскроем скобки и сгруппируем члены при xj.

То есть,
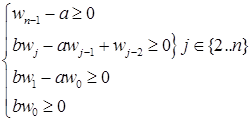
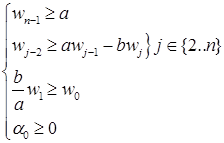
Заметим, что  . Для существования
. Для существования  , по лемме 2.3.4, достаточно выполнения условий
, по лемме 2.3.4, достаточно выполнения условий 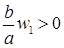 и
и  , то есть,
, то есть,  . Обозначим
. Обозначим  . Так как
. Так как  , то
, то 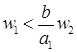 и
и  . Для существования
. Для существования  достаточно доказать существование
достаточно доказать существование  и
и 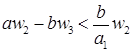 . То есть,
. То есть,  . Обозначим
. Обозначим  . Повторим эту операцию n-2 раза. Получим, что
. Повторим эту операцию n-2 раза. Получим, что  . По лемме 2.3.4,
. По лемме 2.3.4,  существует, если
существует, если  и
и  . Эти условия следуют из того, что
. Эти условия следуют из того, что  и
и  .
.
Таким образом, доказано существование 
■
Теорема 2.3.6. Если минимальный многочлен f-g порождает полуполе то, он либо имеет положительный действительный корень, либо корень  , такой что
, такой что  и последовательность (**), заданная числами p и q, не содержит отрицательных элементов.
и последовательность (**), заданная числами p и q, не содержит отрицательных элементов.
Доказательство. Пусть многочлен f-g не имеет положительных действительных корней, и для всех корней вида  , где
, где  , последовательность (**), заданная числами p и q, содержит отрицательный элемент. Тогда, по теореме 2.3.5, для каждого множителя вида
, последовательность (**), заданная числами p и q, содержит отрицательный элемент. Тогда, по теореме 2.3.5, для каждого множителя вида 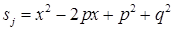 существует многочлен
существует многочлен  , что
, что  . Рассмотрим многочлен
. Рассмотрим многочлен 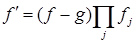 .
.  так как
так как  и
и  . Кроме того
. Кроме того  , а остальные множители многочлена
, а остальные множители многочлена  имеют вид
имеют вид  или
или  . То есть,
. То есть,  . Таким образом
. Таким образом  . По теореме 2.1.1, минимальный многочлен
. По теореме 2.1.1, минимальный многочлен  порождает поле. ■
порождает поле. ■
Теорема 2.3.7. Для комплексных чисел  расширение
расширение  , минимальное соотношение которого имеет положительный корень, является полуполем.
, минимальное соотношение которого имеет положительный корень, является полуполем.
Доказательство. Пусть a' – положительный корень минимального соотношения. Предположим, что 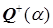 – поле. Тогда существует многочлен f с положительными коэффициентами, делящийся на минимальный многочлен. Значит f (a')=0. Но
– поле. Тогда существует многочлен f с положительными коэффициентами, делящийся на минимальный многочлен. Значит f (a')=0. Но 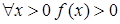 . Значит a' – не является корнем многочлена f. То есть
. Значит a' – не является корнем многочлена f. То есть  – полуполе. ■
– полуполе. ■
Примеры
1. Рассмотрим  . Оно удовлетворяет минимальному соотношению
. Оно удовлетворяет минимальному соотношению  . По теореме 2.3.7,
. По теореме 2.3.7,  - полуполе. Аналогично доказывается, что
- полуполе. Аналогично доказывается, что  – полуполе.
– полуполе.
2.  – полуполе. Для доказательства нужно воспользоваться теоремой 2.3.1.
– полуполе. Для доказательства нужно воспользоваться теоремой 2.3.1.
3. Покажем, что  – полуполе. Во-первых, заметим, что
– полуполе. Во-первых, заметим, что  . Рассмотрим
. Рассмотрим  . По теореме 2.3.7,
. По теореме 2.3.7,  ‑ полуполе. Тогда, по теореме 2.3.1,
‑ полуполе. Тогда, по теореме 2.3.1,  – полуполе.
– полуполе. 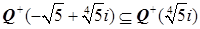 . То есть,
. То есть,  – полуполе.
– полуполе.
4.  , минимальное соотношение которого имеет вид
, минимальное соотношение которого имеет вид  , есть полуполе. Действительно, многочлен
, есть полуполе. Действительно, многочлен  имеет положительный корень, а значит
имеет положительный корень, а значит  - полуполе.
- полуполе.
Теперь приведем примеры полей.
5.  является полем, потому что его минимальный многочлен имеет вид
является полем, потому что его минимальный многочлен имеет вид  .
.
6. Пусть  удовлетворяет минимальному соотношению
удовлетворяет минимальному соотношению  . Его минимальный многочлен
. Его минимальный многочлен  делит
делит  . То есть,
. То есть,  – поле. Несложно видеть, что
– поле. Несложно видеть, что  . Итак,
. Итак,  .
.
7. Пусть  удовлетворяет минимальному соотношению
удовлетворяет минимальному соотношению  . Тогда
. Тогда 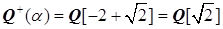 – поле.
– поле.
8. Пусть  , если
, если  , то
, то  – поле. Так как
– поле. Так как  , то
, то  Если
Если  , то
, то  . Рассмотрим последовательность (**), порожденную p и q.
. Рассмотрим последовательность (**), порожденную p и q.  . По теореме 2.3.7,
. По теореме 2.3.7,  – поле.
– поле.
Литература
1. Вечтомов Е.М. Введение в полукольца. – Киров: Изд-во Вятского гос. пед. ун-та, 2000
2. Вечтомов Е.М. О свойствах полутел // Матем. вестник педвузов Волго-Вятского региона. – 2001, вып. 3. – Киров: Изд-во Вят. гос. пед. ун-та. – С. 11-20.
3. Ряттель А.В. Однопорожденные полукольца с делением // Матем. вестник педвузов Волго-Вятского региона. – 2002, вып. 4.– Киров: Изд-во Вятского госпедуниверситета. – С. 39-45.
 2020-01-14
2020-01-14 86
86