Расширения полуполя неотрицательных действительных чисел комплексным числом

Теорема 2.2.1. Любое расширение , где , является полем С.

Доказательство. Пусть ,  и при a > 0. Тогда  находится строго в первой или четвертой четверти комплексной плоскости.

Очевидно, существует натуральное n, что 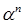 лежит строго во второй или третьей четверти. То есть, , где c < 0, . Значит,  и 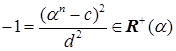. По теореме 2.1.1,  – поле. Очевидно, что . То есть,  является полем С.

Аналогично рассматривается случай                                                ■