Линейные системы с постоянными коэффициентами

 

Пусть А – постоянная квадратная матрица порядка n и рассмотрим соответствующую однородную систему

 

.                                                                                      (4.1)

 

Если n = 1, то (4.1) имеет очевидное решение е^tА_, и решение, которое при t = τ равно ξ, имеет вид е^(t-τ)Аξ. Оказывается, что решение имеет эту форму и в том случае, когда х, ξ являются векторами произвольной конечной размерности и А – квадратная матрица порядка n.

Теорема 4.1. Фундаментальная матрица Ф системы (4.1) дается формулой

 

Ф(t) = е^tА (|t| < 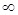),                                                                     (4.2)

 

и решение φ системы (4.1), удовлетворяющее условию

 

 φ(τ) = ξ (|τ | < , | ξ | < ),

 

имеет вид

 

 φ(t) = е^(t-τ)Аξ (|t| < 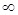).                                                               (4.3)

 

Доказательство. Так как е^(t-Δt)А = е^tА е^ΔtА, то из определения производной легко получаем, что

 

 

Поэтому Ф(t) = е^tА есть решение системы (4.1). Так как Ф(0) = Е, то из (1.8) следует, что det Ф(t) = е^tspА. Итак, Ф – фундаментальная матрица. Теперь формула (4.3) очевидна.

Замечание. Заметим, что выражение  не обязано быть решением системы 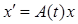, если матрицы А(t) и не коммутируют. Они коммутируют, когда матрица А(t) либо постоянная, либо диагональная.

Интересно исследовать структуру фундаментальной матрицы (4.2). пусть J – каноническая форма матрицы А, указанная в теореме 1.1, и предположим, что Р – неособая постоянная матрица, такая, что АР = PJ.

Тогда

 

                                                             (4.4)

 

и J имеет вид

 

                                                         (4.5)

 

где J₀ – диагональная матрица с элементами λ₁, λ₂,…, λ_q и

 (i = 1, …, s).            (4.6)

 

Далее,

 

                                                  (4.7)

 

и легкое вычисление показывает, что

 

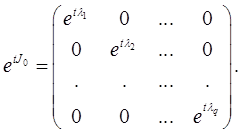                                                 (4.8)

 

Так как , то . Таким образом,

 

                                 (4.9)

где  - квадратная матрица порядка r_i (n = q + r₁ + … + r_s). Поэтому, если известна каноническая форма (4.5), (4.6) матрицы А, то фундаментальная матрица е^tА системы (4.1) дается в явном виде формулой (4.4), в которой е^tJ может быть вычислена из (4.7), (4.8), (4.9).

Другая фундаментальная матрица системы (4.1) такова:

 

 Ψ(t) = е^tАP = P е^tJ.                                                                     (4.10)

 

Пусть матрица Р имеет своими столбцами векторы р₁, …, р_n. Столбцы матрицы Ψ. Которые мы обозначаем через ψ₁, ψ ₂, …, ψ _n, образуют совокупность n линейно независимых решений системы (4.1) и из (4.10) и вида матрицы J получаем

 

, , …, ,

,

,

,

,

.

 

Так как АР = PJ, то векторы р₁, …, р_n удовлетворяют соотношениям

 

Ар₁ = λ₁р₁,…, Ар_q = λ_qр_q,

Ар_q+1 = λ _q+1р_q+1,

Ар_q+2 = р_q+1 + λ _q+1р_q+2,

Ар_n-rs+1 = λ _q+sр _n-rs+1,

Ар_n-rs+2 = р _n-rs+1+λ _q+sр _n-rs+2,

Ар_n = р _n-1+λ _q+sр _n.

 

Решения ψ_j выражаются посредством независимых векторов р₁, …, р_n из предыдущей последовательности уравнений.

Формула вариации постоянных (3.1) в применении к неоднородной системе

 

+b(t) ,                                                                  (4.11)

 

где А – постоянная матрица, дает для решения φ системы (4.11), удовлетворяющего условию φ(τ) = 0, 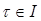, выражение

 

.

 

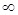Решение φ системы (4.11), удовлетворяющее условию φ(τ) = ξ, где , | ξ |< , имеет вид

 

.