Линейные уравнения с аналитическими коэффициентами

Предположим, что А – квадратная матрица порядка n и b – n-мерный вектор, определенные и аналитические в односвязной области D z-плоскости, и пусть 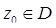. Используя метод последовательных приближений, нетрудно показать, что линейная система

                                                                      (7.1)

при условии

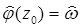
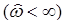
имеет в D единственное аналитическое решение .

В самом деле, пусть  и пусть С – дуга длины L, лежащая в D, соединяющая точки z₀ и z₁ и имеющая непрерывно вращающуюся касательную. Обозначим через s длину дуги вдоль С, начиная от точки z₀. Выберем постоянную К настолько большой, чтобы было | A(z) | < K и | | < K для 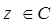. Пусть  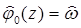и

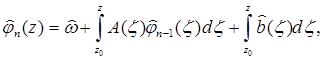
причем интеграл берется вдоль С, так что приближения  определены на С. Нетрудно получить оценки

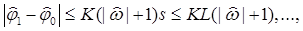
Очевидно, эти оценки справедливы для всех точек z в D, достижимых из z₀ другой длины L, на которой |A(z)| и | | ограничены постоянной K. Отсюда следует, что эти оценки справедливы в каждом фиксированном множестве R, содержащемся в D. Так как каждая функция 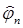 аналитична в R, то из равномерной сходимости  следует, что предельная функция  также аналитична в R. Далее,

Это доказывает утверждение для R и, следовательно, для D.

Кроме того, все теоремы, доказанные в пп. 1.2 и 1.3, будучи существенно алгебраической природы, справедливы для системы (7.1).

Соответственно этому, если n+1 функций а₁, …, а_n, b аналитичны в D, то линейное уравнение порядка n

                                        (7.2)

имеет в D единственное решение, удовлетворяющее условиям

, , …, ,

где w₁, …, w_n – n данных комплексных чисел. Наконец, все результаты п. 2.1 распространяются очевидным образом на случай (7.2).