Линейные системы с периодическими коэффициентами

 

Рассмотрим линейную однородную систему

 

,                                                          (5.1)

 

где А – матрица элементами которой служат непрерывные комплексные функции, и

 

                                                                          (5.2)

 

для некоторой постоянной ω 0. В этом случае (5.1) называется периодической системой с ω-периодом А. Основной результат для таких систем состоит в том, что фундаментальную матрицу можно представить как произведение периодической матрицы с тем же периодом ω и матрицы-решения для системы с периодическими коэффициентами.

Теорема 5.1. Если Ф – фундаментальная матрица для системы (5.1), то тем же свойством обладает матрица

 

Ψ(t) = Ф(t+ω) .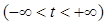

 

Каждой такой матрице Ф соответствует периодическая неособая матрица Р с периодом ω и постоянная матрица R, такие, что

 

 Ф(t) = P(t)e^tR.                                                                            (5.3)

 

Доказательство. Так как

 

,

 

то в силу (5.2)

 

.

 

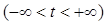Поэтому Ψ есть матрица-решение системы (5.1), и эта матрица фундаментальная, так как det Ψ(t) = det Ф(t+ω) 0 для .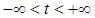

Следовательно, существует постоянная матрица С, такая что

 

 Ф(t+ω) = Ф(t)С,                                                                        (5.4)

 

и, сверх этого, существует постоянная матрица R, такая что

 

 С = е^ωR.                                                                                     (5.5)

 

Из (5.4) и (5.5) получаем

 

 Ф(t+ω) = Ф(t) е^ωR.                                                                    (5.6)

 

Определим матрицу Р по формуле

 

Р(t) = Ф(t) е^-tR.                                                                           (5.7)

 

Тогда, используя (5.6), получаем

 

Р(t+ω) = Ф(t+ω) е^-(t+ω)R = Ф(t) е^ωR е^-(t+ω)R = Ф(t) е^-tR = Р(t).

 

Так как матрицы Ф(t) и е^-tR для 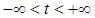 неособые, то Р(t) такая же, и это завершает доказательство.

Значение теоремы 5.1 состоит в том, что значение фундаментальной матрицы Ф на интервале длины ω, например , дает возможность определить Ф на всей числовой прямой. В самом деле, матрица С в (5.5) определяется как формула Ф^-1(0)Ф(ω), а отсюда R определяется как (lnC)/ω. Теперь матрица Р(t) определена на интервале (0,ω) по формуле (5.7), а так как Р(t) имеет период ω, то она определяется на интервале . Теперь матрица Ф определена на интервале 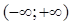 по формуле (5.3).

Если Ф₁ – некоторая другая фундаментальная матрица системы (5.1), для которой выполняется (5.2), то

 

Ф = Ф₁Т,

 

где Т – некоторая постоянная неособая матрица. Из (5.6) следует, что

 

 Ф₁(t+ω)Т = Ф₁(t)Те^ωR,

 

или

 

 Ф₁(t+ω) = Ф₁(t)(Те^ωRТ^-1).                                                          (5.8)

 

Таким образом, в силу (5.8) каждая фундаментальна матрица Ф₁ определяет матрицу Те^ωRТ^-1, подобную е^ωR. Наоборот, если Т – любая постоянная неособая матрица, то существует фундаментальная матрица Ф₁ системы (5.1), такая, что выполняется (5.8). Следовательно, хотя Ф не определяет R однозначно, множество всех фундаментальных матриц системы (5.1), а следовательно матрица А, определяет однозначно все связанные с R величины, инвариантные относительно подобных преобразований. В частности, множество всех фундаментальных матриц системы (5.1) определяет однозначно множество характеристических корней, а именно характеристические корни матрицы С = е^ωR. Обозначим эти корни через λ₁, λ₂,…, λ_n и назовем их мультипликаторами, соответствующими матрице А. Ни один из мультипликаторов не равен нулю, ибо 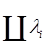= det е^ωR 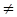0. Характеристические корни матрицы R называются характеристическим показателями.

Интересно выяснить явный вид множества n линейно независимых векторов-решений системы (5.1). Пусть Т – постоянная неособая матрица, такая что матрица Т^-1RТ = J имеет каноническую форму, указанную в теореме 1.1, и положим Ф₁ = ФТ, Р₁ = РТ. Тогда из (5.3) следует

 

 Ф₁(t) = Р₁(t) е^tJ , Р₁(t+ω) = Р₁(t).                                                (5.9)

 

Поэтому, если ρ_i – характеристические корни R, то матрица е^tJ имеет вид

 

 

где

 

 

и

 

 (i = 1, …, s; q+ = n).

 

Очевидно, что λ_i = е^ωρi , и поэтому, хотя сами корни ρ_i определяются неоднозначно, но их действительные части определяются однозначно. Из (5.9) следует, что столбцы φ₁, φ₂, …, φ_n матрицы Ф₁, которые образуют множество n линейно независимых решений системы (5.1), имеют вид:

 

,

,

,

,

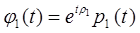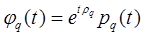,                                          (5.10)

,

,

.

 

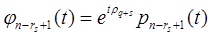В этих формулах р₁, р₂, …, р_n - периодические векторы-столбцы матрицы Р₁.

Из (5.10) очевидно, что если Reρ_i < 0 или, что эквивалентно, | λ_i | < 1, то при 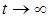 решения φ_i(t) экспоненциально убывают.

Из (5.6) следует, что Ф(ω) = Ф(0)е^ωR, и поэтому λ_i можно рассматривать как характеристические корни матрицы Ф^-1(0)Ф(ω). В частности, если Ф(0) = Е, то е^ωR = Ф(ω) и λ_i являются характеристическими корнями матрицы Ф(ω). Так как

 

                                            (5.11)

 

то n-й корень можно определить из (5.11), если известны n-1 корней λ_i.

Действительная неособая матрица С не обязана иметь действительный логарифм, т.е. не всегда существует действительная матрица В, такая что е^В = С. В самом деле, матрица с одной строкой и одним столбцом С = -1 доставляет соответствующий пример. Однако справедливо утверждение, что для действительной матрицы С существует действительная матрица В, такая, что С² = е^В .

Используя это при доказательстве теоремы 5.1, нетрудно получить следующий результат6 если в системе (5.1) матрица А (t) действительная периодическая с периодом ω, то каждой действительной фундаментальной матрице Ф соответствует действительная матрица Р периода 2ω и действительная постоянная матрица R, такие, что

 

Ф(t) = Р(t)е^tR.