Пусть А – неособая квадратная матрица порядка n из непрерывных функций, определенных на действительном t-интервале I и b – непрерывный вектор на I, не равный тождественно нулю. Система уравнений
 +b(t)
+b(t)  (ЛН)
(ЛН)
называется линейной неоднородной системой порядка n. Если элементы А и b непрерывны и даже измеримы и мажорируются суммируемой функцией на I, то существует единственное решение φ системы (ЛН), для которого
φ(τ) = ξ,
где 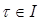 и | ξ | <
и | ξ | <  . Единственность решения следует из того, что если бы существовало два решения φ1 и φ2, то из разность φ = φ1 - φ2 была бы решением однородной системы (ЛО) на I при φ(τ) = 0. Но, по теореме единственности для (ЛО), разность φ должна равняться на I нулю тождественно и, следовательно, φ1 = φ2.
. Единственность решения следует из того, что если бы существовало два решения φ1 и φ2, то из разность φ = φ1 - φ2 была бы решением однородной системы (ЛО) на I при φ(τ) = 0. Но, по теореме единственности для (ЛО), разность φ должна равняться на I нулю тождественно и, следовательно, φ1 = φ2.
Если известна фундаментальная матрица Ф системы (ЛО), то легко найти решение системы (ЛН).
Теорема 3.1. Если Ф - фундаментальная матрица для системы (ЛО), то функция

 (3.1)
(3.1)
есть решение системы (ЛН), удовлетворяющее начальному условию
φ(τ) = 0 (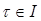 ).
).
Доказательство получается непосредственно при помощи прямой проверки.
Интуитивные соображения, с помощью которых можно получить выражение (3.1), заключаются в следующем6 для каждого постоянного вектора с функция Фс является решением системы (ЛО). Метод состоит в том, что мы рассматриваем с как функцию, определенную на I, и находим, какой должна быть с (если она существует), для того, чтобы функция φ = Фс была решением неоднородной системы (ЛН).
Пусть φ = Фс – решение системы (ЛН). Тогда
 =
= 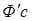 +Ф
+Ф 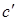 =АФс + Ф
=АФс + Ф 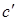 = А φ + Ф
= А φ + Ф  = А φ + b,
= А φ + b,
где последнее равенство следует из (ЛН). Поэтому Ф 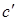 = b, или
= b, или
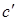 =
=  b.
b.
Последнее уравнение всегда разрешимо, причем если с(τ) = 0, то

 .
.
Итак, φ определяется по формуле (3.1).
Легко видеть, что в условиях теоремы 3.1 решение системы (ЛН), удовлетворяющее условию φ(τ) = ξ (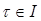 и | ξ | <
и | ξ | <  ), дается в виде
), дается в виде
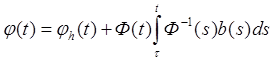
 , (3.2)
, (3.2)
где  - решение системы (ЛО), удовлетворяющее условию
- решение системы (ЛО), удовлетворяющее условию
φh(τ) = ξ.
Формула (3.1) (или (3.2)) называется формулой вариации постоянных для системы (ЛН).
Заметим, что формулу (3.1) можно записать в виде

 ,
,
где Ψ – фундаментальная матрица системы
 ,
,
сопряженной системе (ЛО). Другая форма записи формулы (3.1) такова:
 ,
,
однако здесь необходимо ограничение 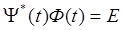 .
.
 2020-01-14
2020-01-14 100
100








