Анализ современных методов спектрального оценивания мгновенного спектра

Из теории спектрального анализа известно, что существует два эквивалентных определения энергетического спектра (спектра мощности) сигнала [1]:

1. Квадрат модуля функции S

 

                           (1.10)

 

2. Обратное преобразование Фурье автокорреляционной последовательности [1]:

 

                            (1.11)

 

Отметим, что вычисления, проведенные согласно (1.10) и (1.11) для сигналов, частота которых изменяется в широком интервале частот за время регистрации Т, позволяют констатировать наличие в спектре определенной гармоники, соответствующей данной частоте, но не позволяют зафиксировать, в какой момент времени появилась данная гармоника, поскольку вычисление спектра S() осуществляется интегрированием по всевозможным значениям переменной [0,T]. Осознание того факта, что спектр, определенный таким образом, не позволяет определить закон изменения частоты сигнала f=f(t), привело к созданию нового понятия цифрового спектрального анализа – понятию мгновенного спектра. На один из возможных способов введения этого понятия указывает (1.10). Проведем разбиение интервала регистрации [0,Т] на N подинтервалов, длиной T/N, что позволяет провести вычисление N значений функции S_i()

 

                            (1.12)

 

где j = 1,..,N. Вычисленный набор S ((у) позволяет судить об эволюции спектра сигнала во времени. Данный подход к определению МС используется нами в дальнейшем. Отметим, что увеличение числа интервалов разбиения N приводит к необходимости вычисления спектров на реализациях сигнала малой длительности. Получение устойчивых (робастных) спектральных оценок, не обеспечиваемых классическими методами, требует применения неклассических методов спектрального оценивания, обсуждение которых проводится ниже.

Следует отметить, что исторически понятие МС было введено по аналогии с (1.11) как функция распределения мощности (энергии) p(t, f)

 

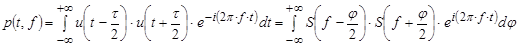 (1.13)

 

С физической точки зрения функция 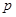(t,f) определяет разность энергий двух бесконечно близких точек на плоскости (t,f). Полезно привести свойства функции  (t,f), которые поясняют ее физический смысл:

 

 (1.14)

 

то есть интеграл от функции p(t, f), взятый по частоте, определяет мощность (энергию) сигнала в данный момент времени.

 

 (1.15)

 

то есть интеграл от функции p(t,f), взятый по времени, определяет спектральную плотность энергии на частоте f. Другие определения МС по Рихачеку, по Пейнджу, тесно связанные с функцией неопределенности, широко применяемой в импульсной радиолокации, можно найти в [11].

Проведем сравнение объема необходимых вычислений согласно (1.11) и (1.15). Предположим, что сигнал, значения амплитуды которого заданы в N точках, разбивается на k интервалов по N₁ точек в каждом. Для вычисления спектра по (1.11), как правило, используется алгоритм БПФ [11]. Количество арифметических операций, при выполнении БПФ на N₁ точках составляет N₁log₂N₁. Для нахождения МС по (1.14) необходимо провести вычисление автокорреляционной функции в N₁ точках согласно (1.12). Вычисление одного значения автокорреляционной функции требует выполнения N₁ операции умножения и N₁ операции сложения. Следовательно, с учетом симметрии автокорреляционной функции, вычисление N₁, ее значений требует операций, последующее вычисление БПФ составляет  операций [12]. Таким образом, проведенная оценка свидетельствует, что первый способ требует меньшего количества арифметических операций, поэтому в дальнейшем для оценки мгновенных спектров используется (1.11).

Как очевидно, определение закона изменения частоты PC во времени будет тем более точным, чем меньше длительность интервала, на котором производится анализ PC. Уменьшение длины интервала, в свою очередь, проявляет основную проблему, стоящую перед цифровым спектральным анализом получение робастных оценок спектра и высокого частотного разрешения для последовательностей данных конечной (особенно малой) длительности. Два эквивалентных подхода к нахождению спектральной плотности мощности, основанных как на прямом ее вычислении по исходной последовательности данных (1.10), так и на Фурье–преобразовании автокорреляционной последовательности (1.11), позволяют оценить выборочные спектры, которые оказываются статистически несостоятельными, так как среднеквадратичная ошибка этих оценок сравнима по величине со средним значением оценки [11]. Поиски способов устранения отмеченного недостатка, активно проводившиеся в последнее десятилетие, привели к развитию нескольких методов спектрального оценивания, основанных на различных математических подходах: классических, параметрических, непараметрических.

К классическим методам относятся методы, основанные на прямом преобразовании Фурье данных с последующим усреднением по нескольким спектрам (периодограммные) и методы, основанные на оценке усредненной автокорреляционной последовательности исходных данных, получаемой Фурье–преобразованием (коррелограммные). При использовании классических методов оценивания спектра приходится принимать множество компромиссных решений с целью получения робастных спектральных оценок с максимально возможным разрешением. К таким решениям относятся выбор соответствующих функций окна для взвешивания данных и корреляционных функций и параметров усреднения во временной и частотной областях [19]. Устойчивые результаты и хорошая точность, под которыми понимаются малые спектральные флюктуации и незначительное смещение вычисленных значений спектра относительно его истинных значений на всех частотах, достигаются для сигналов, удовлетворяющих условию

 

>>1,

 

где Т – время регистрации, В – разрешение по частоте [12]. Эти компромиссы теоретически обоснованы лишь для гауссовых случайных процессов. Рекомендации по выбору того или иного метода спектрального оценивания и функции окна в случае негауссовых случайных процессов, а также сигналов со сложным законом изменения частоты, к которым относится PC, получаемые при внутри–ствольных измерениях, отсутствуют. Подробную обширную информацию по классическим методам спектрального оценивания можно найти в [17–19,13–16]. Использование периодограммных и коррелограммных методов (понимаемых в смысле [17] для вычисления мгновенных спектров частотно–модулированных сигналов, к которым относятся PC, и возможности восстановления с их помощью закона изменения частоты сигнала, нам неизвестны. Отметим, что понятия периодиограммных и коррелограммных методов, применяемых нами для оценивания мгновенных спектров сигнала, созвучны с названиями корреляционных и ковариационных методов, используемых в работе [18], для спектрального оценивания на основе решетчатой структуры. Однако, суть их принципиально различна, так как в [18] они применяются только для оценивания корреляционной матрицы, использующейся в дальнейшем в параметрических методах спектрального оценивания (см. ниже), но не спектра сигнала.

Получение более точных оценок спектральных характеристик сигнала (по сравнению с достигаемыми с помощью классических методов) потенциально возможно при использовании параметрических методов. В данных методах исходная временная последовательность рассматривается как выходная последовательность каузального фильтра, на вход которого подается возбуждающая последовательность [16]. Модель временного ряда, пригодная для аппроксимации большинства детерминированных и стохастических сигналов с дискретным временем, описывается как

 

    (1.16)

 

где u[n] – последовательность на выходе каузального фильтра, y[n] – входная возбуждающая последовательность, h[k] – передаточная функция фильтра.

В зависимости от условий, накладываемых на коэффициенты, входящие в модель цифрового ряда, получают различные параметрические модели. Модель (1.16) в предположении, что последовательность у[п] является белым шумом имеет название модель авторегрессии – скользящего среднего (АРСС), здесь коэффициенты a[k] характеризуют авторегрессионую часть этой модели, а параметры b[k] – ее часть, соответствующую скользящему среднему. Если все коэффициенты a[k], называемые авторегрессиоными параметрами (АР–параметрами), за исключением а[0] равного единице, положить равными нулю, то тогда модель временного ряда принимает вид:

 

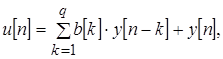                                            (1.17)

 

модель становится строго процессом скользящего среднего порядка q (CC(q) –процессом).

Если все коэффициенты b[k], называемые параметрами скользящего среднего (СС – параметры), положить равными нулю, тогда модель временного ряда принимает вид:

 

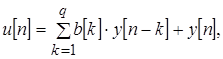                                            (1.18)

 

модель становится чисто авторегрессионой моделью (АР–модель). Величины р и q – называются параметрами модели APCC(p,q) (р – параметр авторегрессионной модели, q – параметр скользящего среднего).

Из теории линейных систем [134] известна связь между линейной импульсной характеристикой h[k] и коэффициентами a[k], b[k], выражаемая через Z–преобразование. Последовательностям h[k], a[k], b[k] ставятся в соответствие функции H(z) (дискретная системная функция фильтра [32]), A(z), B(z) (Z– преобразование последовательностей a[k], b[k]), между которыми существует следующая связь

 

,                                                                     (1.19)

 

где A(z), B(z), H(z) определяются как

 

 (1.20)

 (1.21)

 (1.22)

 

здесь z – произвольное комплексное число.

Условием устойчивости данного каузального минимально–фазового фильтра является нахождение нулей полиномов A(z), B(z) внутри единичной окружности в Z–плоскости. Z–преобразование выходной автокорреляционной последовательности u[n] – P_uu (z) и Z–преобразование входной автокорреляционной последовательности случайного процесса y[n] – P_yy (z) связаны следующим соотношением [5]

 

, (1.23)

 

где знак * означает комплексное сопряжение.

Предполагая, что входная последовательность является белым шумом с нулевым средним и дисперсией pw, так что pui^Pw, выражение (1.17) принимает вид:

 

                                       й(1.24)

 

Спектральную плотность мощности для АРСС(р,о)–модели получают из (1.24) заменой z , которую масштабируют на длительность интервала Т

 

 (1.25)

 

где полиномы A(f), B(f) определяются выражениями:

 

 (1.26)

 (1.27)

 

векторы комплексных синусоид е (f),e (f) и векторы параметров a, b имеют вид:

 

                                                   

                                       (1.28)

 

знак Н означает операцию эрмитова сопряжения.

Полагая в (1.28) р равным нулю, получаем выражение для спектральной плотности мощности CC(q) – npoцecca

 

 (1.29)

 

Полагая в (1.25) q равным нулю, получаем выражение для спектральной плотности мощности АР(р)–процесса

 

 (1.30)

 

Таким образом, как видно из (1.25), (1.29), (1.30) для оценки спектров необходимо вычисление параметров модели a[k], b[k] по известной автокорреляционной последовательности, что приводит к системе уравнений Юла–Уолкера для APCC(p,q), AP(p), СС(о)–процессов, для решения которой используют рекурсивные алгоритмы, связывающие АР–параметры более высокого порядка с параметрами более низкого порядка [31]. В связи с тем, что авторегрессионные спектры имеют более острые пики (это часто связано со спектральным разрешением) и уравнения Уюла–Уолкера для АР–процесса линейны, в отличие от APCC(p,q) и СС(о)–моделей, данное направление наиболее исследовано. Следует отметить, что свойства АР(р)–процесса и его спектра породили другие его названия – метод максимальной энтропии [25,26] и метод линейного предсказания [21,22]. Подход к трактовке коэффициентов a[k], b[k], как коэффициентов отражения при интерпретации измерений физических параметров акустической трубы [25,26] и сейсмических данных, получаемых при исследовании слоистой структуры Земли, привел к созданию популярного в настоящее время метода оценки АР–параметров по последовательности оценок коэффициентов отражения – алгоритм Берга [14,15]. Помимо алгоритма Берга в [13] рассмотрены другие алгоритмы оценки коэффициентов отражения – геометрический алгоритм, рекурсивное оценивание по методу максимального правдоподобия, предложенные в [14,15]. В основе их лежит предположение о том, что из всех коэффициентов отражения a[k] только коэффициент а[р], равный коэффициенту отражения, зависит от автокорреляционной функции.

Другой подход состоит в минимизации ошибки линейного предсказания методом наименьших квадратов по всем коэффициентам линейного предсказания. В зависимости от способа линейного предсказания различают алгоритмы с раздельным и комбинированным линейным предсказанием вперед и назад [13] – ковариационный и модифицированный ковариационный методы.

Основной трудностью реализации данных алгоритмов спектрального оценивания является неопределенность в выборе оптимального порядка фильтра. Поэтому решение о выборе того или иного порядка фильтра принимается заданием того или иного критерия ошибки, сравнением с которым определяется требуемый порядок модели. Малый порядок модели приводит к сильно сглаженным спектральным оценкам, излишне большой – к появлению ложных пиков. Следовательно, выбор порядка модели, определяющий разрешение спектра

и его дисперсию, эквивалентен выбору между разрешением и дисперсией для классических методов спектрального оценивания. Для выбора порядка модели предложено несколько критериев, подробно обсуждаемых в [14], поэтому ограничимся их кратким упоминанием:

1. Окончательная ошибка предсказания (ООП) (выбор порядка АР–процесса выбирается из требования минимизации средней дисперсии ошибки).

2. Информационный критерий Акаике (ИКА) (порядок модели определяется посредством минимизации некоторой теоретической информационной функции).

3. Авторегрессионный передаточной функции критерий (АПФК) (порядок модели выбирается равным порядку, при котором оценка разности среднего квадрата ошибки между истинным фильтром предсказания ошибки и оцениваемым фильтром минимальна).

Результаты оценивания спектра при использовании критериев ООП, ИКА, АПФК близки друг к другу в случае реальных данных. Однако в случае коротких записей данных ни один из критериев не обеспечивает удовлетворительных результатов [13]. Точного аналитического решения задачи о выборе порядка модели в настоящее время нет, поэтому необходимо проведение численных экспериментов с имитационным PC для выбора оптимального порядка модели.

Модель APCC(p,q) имеет больше степеней свободы, чем АР(р)–модель, что позволяет ожидать более адекватную передачу формы спектров. Однако основной сложностью данного метода является необходимость решения системы нелинейных уравнений, связывающих коэффициенты a[k], b[k] и автокорреляционную последовательность исходных данных. Методы решения нелинейных уравнений, основанные на интерационных алгоритмах, требуют большого количества вычислений, но самое главное, они зачастую могут не обеспечить сходимость к верному решению, поэтому были разработаны методы, основанные на методе наименьших квадратов, позволяющие провести линеаризацию системы уравнений и раздельно оценить АР-параметры, а затем СС-параметры.

Для оценки АР-параметров используется один из вариантов модифицированного уравнения Юла-Уолкера [16]. Так же неопределенным остается вопрос о выборе параметра модели, так как модификация ИКА, проведенная для АР-модели, проверена только для самых простых случаев.

Известен также метод моделирования выборочной последовательности данных в виде линейной комбинации экспоненциальных функций – метод Про–ни. то есть используется аппроксимация последовательных данных детерминированной экспоненциальной моделью [14]. Математически данный метод формулируется следующим образом. Пусть имеется N точечная последовательность данных и[1], u[N]. В методе Прони эта последовательность оценивается р–членной моделью комплексных экспонент:

 

  (1.31)

 

где , – время регистрации, _k, — амплитуда и коэффициент затухания k–ой комплексной экспоненты, — частота и начальная фаза k–ой экспоненты. Функцию  удобно представить в виде

 

 (1.32)

 

где

 

 (1.33)

 

Здесь h_к – комплексная амплитуда, независящая от времени, Z_к – комплексная экспонента, зависящая от времени.

Найдем квадрат ошибки интерполяции

 

 (1.34)

 

Ошибку [n] минимизируют по параметрам h_к,z_к и числу компонент р. Если значение р неизвестно, то задача становится нелинейной. Решение нелинейной задачи требует применение метода Ньютона или метода градиентного спуска, которые наряду с большим объемом вычислений могут не обеспечивать сходимость к истинному решению. Эти трудности привели к разработке субоп–тимальных процедур минимизации, которые получили название – метод наименьших квадратов Прони [15]. Обычный метод наименьших квадратов Прони может быть модифицирован при использовании незатухающих комплексных синусоид ( =0) [25]. Процедура Прони завершается вычислением оценок параметров, которые определяют амплитуду, коэффициент затухания, частоту и фазу. В [13] предложено определять спектр Прони в терминах экспоненциальной аппроксимации 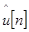, а не в терминах временной последовательности u[n]. Спектральная плотность энергии Прони определяется как

 

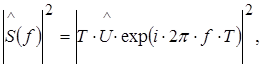                                    (1.35)

 

где                                              (1.36)

 

для односторонней функции [n] (то есть,  [n]=0 при n<0),

 (1.37)

 

для двусторонней функции  [n]. Известны приложения метода Прони к анализу динамики солнечных пятен и определения резонансных пиков в диаграммах эффективной площади рассеяния радиолокационных целей [12]. Исследования вопроса применимости данного метода к анализу ЧМ сигналов нам неизвестны.

К другому классу методов спектрального оценивания одномерных временных рядов относятся непараметрические методы – метод минимальной дисперсии (МД), и методы, основанные на гармоническом разложении Писаренко, – метод классификации множественных сигналов MUSIC (multipay signal classification) и метод оценки собственных векторов автокорреляционной матрицы или матрицы данных EV (eigenvector) [26].

Спектральная оценка, полученная методом МД, определяется выражением

 

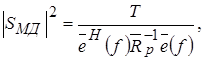 (1.38)

 

где – матрица, обратная известной или оцененной автокорреляционной матрице 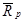размером (р+1)х(р+1),

 

                                 (1.39)

                  (1.40)

 

Алгоритм метода МД и его программная реализация приведены в [14]. Следует отметить, что оценка спектральной мощности, получаемая согласно (1.30), не характеризует полную мощность измеряемого процесса, так как обратное преобразование Фурье спектральной оценки метода МД не соответствует истинной автокорреляционной функции. То есть спектральную оценку по методу МД можно считать спектральной в том смысле, что она описывает относительные интенсивности компонент частотного спектра, высота которых прямо пропорциональна мощности синусоид, присутствующих в исходном сигнале.

Этот класс методов спектрального оценивания основан на разделении информации, содержащейся в автокорреляционной матрице или матрице данных, на два векторных подпространства – подпространство сигнала и подпространство шума. Анализ собственных векторов матриц, относящихся к указанным

подпространствам, дает возможность определять различные функции от данных векторов, имеющие острые пики на частотах синусоид, присутствующих в исходном сигнале. Считается, что данные методы обеспечивают лучшее спектральное разрешение, чем АР-методы и метод Прони, особенно при низком отношении сигнал/шум [13].

Спектральная оценка при использовании собственных векторов подпространства сигнала получается из решения матричного уравнения

 

 (1.41)

 

относительно вектора неизвестных мощностей [14], любым известным методом решения линейных уравнений с комплексными коэффициентами.

Спектральная оценка методом MUSIC, основанным на использовании собственных векторов подпространства шума с равномерной весовой обработкой, определяется как

 (1.42)

 

где  (1.43)

 

– собственный вектор подпространства шума.

Используя весовые множители  (где  – собственное значение, соответствующее собственному вектору ), получаем алгоритм EV спектрального оценивания

 

               (1.44)

 

Основным способом для принятия решения о значении числа М, соответствующего количеству собственных векторов подпространства сигнала, является анализ относительных величин собственных значений (сингулярных чисел) разложения автокорреляционной матрицы или матрицы данных по сингулярным значениям или использование модифицированного ИКА [14]. Следует отметить, что получаемая оценка, как и в методе МД, не является истиной спектральной плотностью мощности, так как обратное преобразование Фурье от (1.35), (1.36) не равно автокорреляционной последовательности. Исследования возможности применения непараметрических методов к анализу ЧМ сигналов, а также применимости данных методов и модифицированного ИКА при наличии небелого шума нам неизвестны.

В заключении обзора современных методов спектрального оценивания следует отметить, что проверка их частотного разрешения и статистической устойчивости выполнена либо на тестовых сигналах с известным составом (как правило, синусоиды плюс белый шум), либо для сигналов с медленно меняющимися параметрами (гидролокация, сейсмические сигналы, задачи пеленгации). Применительно к анализу сигналов с частотно–временными параметрами, аналогичными параметрам PC в задачах определения параметров поступательного движения снаряда в стволе, исследования ранее не проводились.