2020-01-14
91
Как известно, существует два вида уравнений ОТО:
; (2.1)
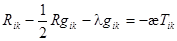, (2.2)
где: 
– тензор Риччи, свертка тензора кривизны Римана-Кристоффеля 
; 
– тензор энергии-импульса материи; 
– метрический тензор четырехмерного пространства-времени; 
– скаляр кривизны, свертка тензора Риччи;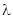 
– космологическая постоянная; 
– постоянная Эйнштейна;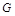 
– постоянная тяготения Ньютона; i, j, k, l =1,2,3,4.
Для однозначного выбора уравнений Эйнштейна взята глобальная евклидовость Вселенной, математическим выражением которой является равенство
. (2.3)
Поскольку для реальной Вселенной, заполненной материей с ненулевой плотностью, 
, то становится очевидным факт невыполнения равенства (2.1). Таким образом, плоскую в глобальных масштабах Вселенную могут описывать только уравнения (2.2). При этом отклонения от плоского пространства-времени под действием гравитирующих масс представляются в виде суммы
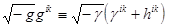, (2.4)
|
|
|
которая соответствует заданию тензорного гравитационного поля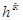 
на фоне плоского материального мира в произвольных координатах с метрикой 
.
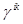Другим, не менее важным свойством Вселенной является ее однородность и изотропность в больших масштабах. Математически это свойство представляется в виде равенства нулю ковариантной производной тензорной плотности 
и следствий этого равенства:
, (2.5)
где точкой с запятой обозначена ковариантная производная, а запятой – обычная.
После этого уравнения (2.2) с помощью преобразования (2.4) и условия (2.5) – наподобие калибровочного условия Лоренца в электродинамике (но здесь обязательного!) – приводятся к уравнениям полевой формулировки ОТО:
, (2.6)
где: 
– оператор Даламбера (даламбертиан); 
– тензор энергии-импульса материи вместе с гравитационным полем.
Условия (2.5) по своему математическому смыслу эквивалентны добавлению к традиционным уравнениям ОТО четырех недостающих до полноты системы уравнений, после чего задача объяснения реальных свойств Вселенной становится разрешимой без каких-либо дополнительных и необоснованных допущений.
