1. Знайти число розв’язків системи рівнянь (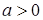 )
)
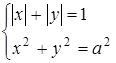
Розв’язання. Побудуємо графіки функцій 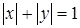 (квадрат зі стороною
(квадрат зі стороною 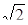 ) та
) та 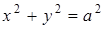 . Члени сім’ї функцій
. Члени сім’ї функцій 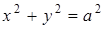 - гомотетичні кола (з центром гомотетії (0,0)).
- гомотетичні кола (з центром гомотетії (0,0)).
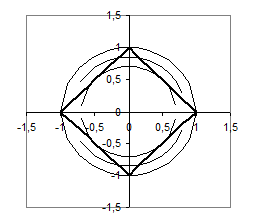
Рис.1.3.1
Якщо коло лежить всередині квадрата, то розв’язків немає.
Якщо коло вписане в квадрат, то з’являються розв’язки. В цьому випадку з теореми Піфагора: 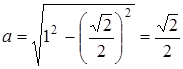 .
.
При 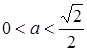 система немає розв’язків, при
система немає розв’язків, при 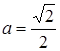 система має 4 розв’язки. Далі зі збільшенням
система має 4 розв’язки. Далі зі збільшенням 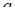 (
(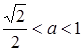 ) кожна сторона квадрата має дві спільні точки перетину з колом (всього 8 розв’язків).
) кожна сторона квадрата має дві спільні точки перетину з колом (всього 8 розв’язків).
При 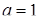 квадрат вписаний в коло, маємо 4 розв’язки. При
квадрат вписаний в коло, маємо 4 розв’язки. При 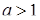 розв’язків немає. Відповідь: при
розв’язків немає. Відповідь: при 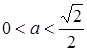 розв’язків немає, при
розв’язків немає, при 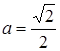 - 4 розв’язки, при
- 4 розв’язки, при 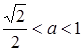 - 8 розв’язків, при
- 8 розв’язків, при 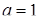 - 4 розв’язки, при
- 4 розв’язки, при 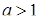 розв’язків немає.
розв’язків немає.
2. При яких дійсних значеннях 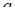 система
система
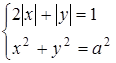
має 8 різних розв’язків?
Розв’язнання. Побудуємо графіки функцій 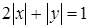 (ромб зі стороною довжиною
(ромб зі стороною довжиною 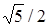 ) та
) та 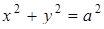 . Члени сім’ї функцій
. Члени сім’ї функцій 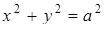 - гомотетичні кола (з центром гомотетії (0,0)).
- гомотетичні кола (з центром гомотетії (0,0)).
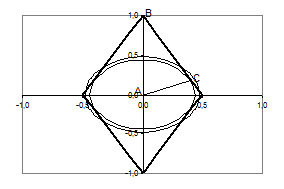
Рис.1.3.2
Знайдемо значення параметра 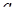 , при якому коло дотикається до ромба.
, при якому коло дотикається до ромба.
З прямокутного трикутника (зі сторонами 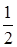 та 1) знайдемо
та 1) знайдемо 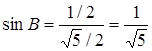 , тоді з трикутника АВС
, тоді з трикутника АВС 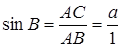 , звідки
, звідки 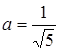 .
.
Зі збільшенням 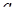 система буде мати 8 розв’язків (8 точок перетину кола з ромбом). А при
система буде мати 8 розв’язків (8 точок перетину кола з ромбом). А при 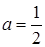 система буде мати 4 розв’язки (4 точки перетину з ромбом). Отже,
система буде мати 4 розв’язки (4 точки перетину з ромбом). Отже, 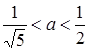 . Відповідь:
. Відповідь: 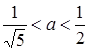
3. Визначити, при яких 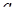 система рівнянь
система рівнянь
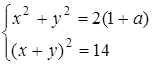
має точно два розв’язки.
Розв’язання. Перепишемо систему рівнянь у вигляді
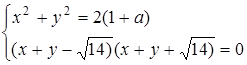
Перше рівняння визначає гомотетичні кола (з центром гомотетії (0,0) та радіусом 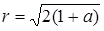 ). Друге рівняння - об’єднання двох прямих:
). Друге рівняння - об’єднання двох прямих: 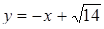 ,
, 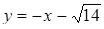 . Побудуємо прямі та кола на графіку.
. Побудуємо прямі та кола на графіку.
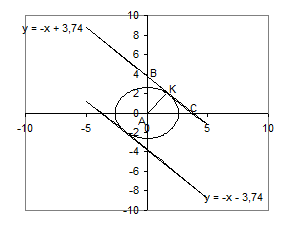
Рис.1.3.3
Система буде мати точно 2 розв’язки, коли коло дотикається двох прямих. Знайдемо параметр 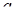 . З
. З 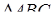 гіпотенуза
гіпотенуза 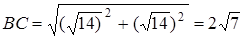 ,
, 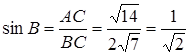 . З
. З 
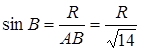 , тоді
, тоді 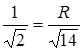 ,
, 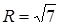 . Остаточно знаходимо
. Остаточно знаходимо 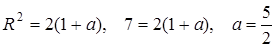 . Відповідь:
. Відповідь: 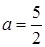 .
.
4. Для кожного від’ємного числа 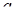 розв’язати нерівність
розв’язати нерівність 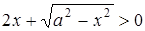 .
.
Розв’язання. Перепишемо нерівність у вигляді 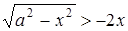 . Побудуємо графіки
. Побудуємо графіки 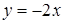 та
та 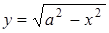 . Членами сім’ї функцій
. Членами сім’ї функцій 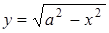 є гомотетичні півкола (центр гомотетії - точка (0,0)). З нерівності випливає, що півкола повинні лежати вище прямої
є гомотетичні півкола (центр гомотетії - точка (0,0)). З нерівності випливає, що півкола повинні лежати вище прямої 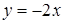 .
.
Кутовий коефіцієнт прямої 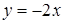 дорівнює -2. Тоді
дорівнює -2. Тоді 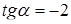 ,
, 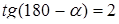 , із
, із 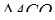 :
: 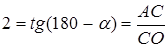 ,
, 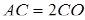 .
.
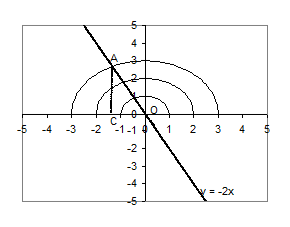
Рис.1.3.4
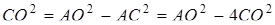 , звідки
, звідки
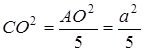 ,
, 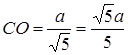 .
.
Розв’язком нерівності для кожного від’ємного числа 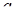 буде проміжок
буде проміжок 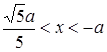 . Відповідь:
. Відповідь: 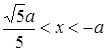 .
.
5. Скільки розв’язків в залежності від 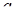 має рівняння
має рівняння 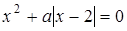 .
.
Розв’язання. Перепишемо рівняння у вигляді 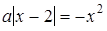 . Побудуємо графіки функцій
. Побудуємо графіки функцій 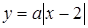 (гомотетичні кути з вершиною в точці (2,0)) та
(гомотетичні кути з вершиною в точці (2,0)) та 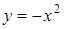 . При
. При 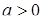 графіки наведені на рисунку 1.3.5
графіки наведені на рисунку 1.3.5
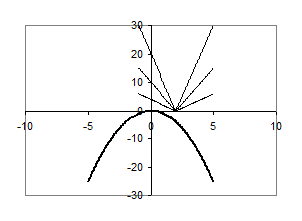
Рис.1.3.5
З рис.1.3.5 видно, що при 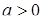 спільних точок графіки не мають, рівняння розв’язків немає.
спільних точок графіки не мають, рівняння розв’язків немає.
При 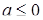 графіки
графіки 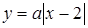 та
та 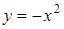 наведені на рисунку 1.3.6.
наведені на рисунку 1.3.6.
З рис.1.3.6 видно, що при 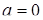
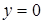 ,
, 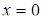 - 1 розв’язок;
- 1 розв’язок;
при 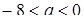 - 2 точки перетину графіків (2 розв’язки);
- 2 точки перетину графіків (2 розв’язки);
при 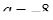 - 3 точки перетину графіків (3 розв’язки);
- 3 точки перетину графіків (3 розв’язки);
при 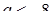 - 4 точки перетину графіків (4 розв’язки).
- 4 точки перетину графіків (4 розв’язки).
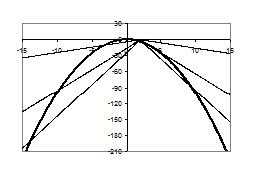
Рис.1.3.6
Відповідь: при 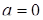
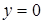 ,
, 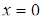 - 1 розв’язок; при
- 1 розв’язок; при 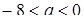 - 2 розв’язки; при
- 2 розв’язки; при 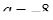 - 3 розв’язки; при
- 3 розв’язки; при 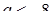 - 4 розв’язки.
- 4 розв’язки.
6. При яких значеннях 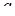 криві
криві 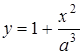 та
та 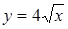 мають тільки одну спільну точку?
мають тільки одну спільну точку?
Розв’язання. Необхідно розв’язати рівняння 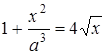 або
або 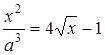 . Побудуємо графіки функцій
. Побудуємо графіки функцій 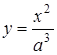 (гомотетичні вітки парабол з центром гомотетії (0,0)) та
(гомотетичні вітки парабол з центром гомотетії (0,0)) та 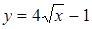 . ОДЗ рівняння:
. ОДЗ рівняння: 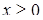 .
.
При 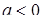 маємо 1 розв’язок.
маємо 1 розв’язок.
Розглянемо випадок дотику двох графіків.
Запишемо рівняння дотичних до кожного з графіків в точці 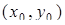 :
:
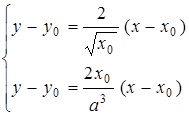 , звідси
, звідси 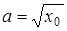 .
.
Підставляємо 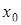 в рівняння
в рівняння 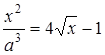 , тоді
, тоді 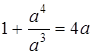 ,
, 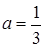 .
.
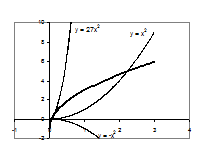
Рис.1.3.7
Відповідь: 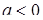 або
або 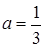 .
.
7. При яких значеннях параметра 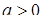 рівняння
рівняння 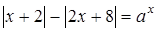 має єдиний розв’язок, більше одного розв’язку, немає розв’язків?
має єдиний розв’язок, більше одного розв’язку, немає розв’язків?
Розв’язання. Побудуємо графіки функцій 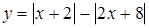 та
та  .
.
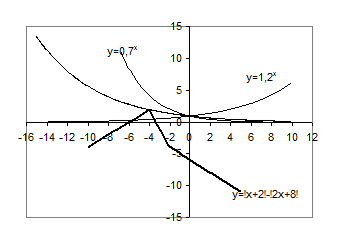
Рис.1.3.8
Розв’яжемо рівняння на проміжку 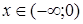 для того, щоб знайти точку дотику функцій.
для того, щоб знайти точку дотику функцій.
Якщо 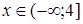 , то
, то 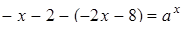 ,
, 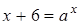 , при
, при 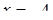
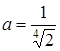 .
.
Таким чином, при 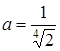 - 1 розв’язок, при
- 1 розв’язок, при 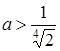 - точки перетину графіків є (більше одного розв’язку), при
- точки перетину графіків є (більше одного розв’язку), при 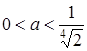 - немає точок перетину графіків (немає розв’язків).
- немає точок перетину графіків (немає розв’язків).
Відповідь: при 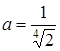 - 1 розв’язок, при
- 1 розв’язок, при 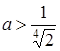 - більше одного розв’язку, при
- більше одного розв’язку, при 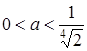 немає розв’язків.
немає розв’язків.
Задачі для самостійної роботи
1. При яких с система має хоча б один розв’язок?
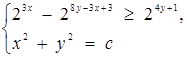
Розв’язання. Спростимо нерівність системи. Маємо 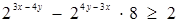 . Нехай
. Нехай 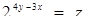 . Тоді
. Тоді 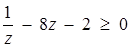 . Звідси з урахуванням того, що
. Звідси з урахуванням того, що 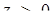 , одержимо
, одержимо 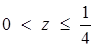 . Запишемо
. Запишемо 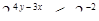 , тобто
, тобто 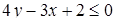 . Таким чином, початкова система рівносильна такій:
. Таким чином, початкова система рівносильна такій:
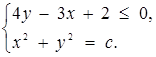
Графіком першої нерівності цієї системи є півплощина з межею 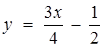 (рис.1.3.9).
(рис.1.3.9).
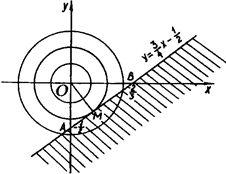
Рис.1.3.9
Очевидно система може мати розв’язки, якщо 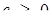 . Тоді рівняння
. Тоді рівняння
х 2 + у 2 = с задає сім’ю гомотетичних кіл з центром в точці О (0; 0). Рисунок підказує, що якщо радіус кола не менше довжини відрізка ОМ, тобто відстань від точки О до межі півплощини, то система має розв’язки. Маємо 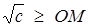 . З
. З 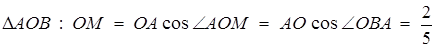 . Звідси
. Звідси 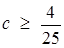 .
.
Відповідь: 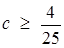 .
.
2. Скільки розв’язків має система в залежності від параметра а?
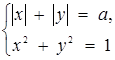
Розв’язання. При 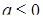 система розв’язків не має. При фіксованому
система розв’язків не має. При фіксованому 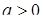 графіком першого рівняння є квадрат з вершинами (а; 0), (0; - а), (-а; 0), (0; а). Таким чином, членами сім’ї
графіком першого рівняння є квадрат з вершинами (а; 0), (0; - а), (-а; 0), (0; а). Таким чином, членами сім’ї 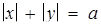 є гомотетичні квадрати (центр гомотетії - точка О ( 0; 0)).
є гомотетичні квадрати (центр гомотетії - точка О ( 0; 0)).
Якщо квадрат (рис.1.3.10) знаходиться в колі 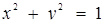 система розв’язків не має.
система розв’язків не має.
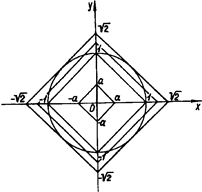
Рис.1.3.10
Зі збільшенням а (квадрат "роздувається") розв’язки з’являються лише в той момент, коли квадрат буде вписаним в коло. В цьому випадку (а = 1) розв’язків буде чотири. Далі, при 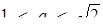 кожна сторона квадрата має дві спільні точки з колом, тоді система буде мати вісім розв’язків. При
кожна сторона квадрата має дві спільні точки з колом, тоді система буде мати вісім розв’язків. При 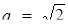 коло буде вписане в квадрат, тобто розв’язків стане знов чотири. Очевидно при
коло буде вписане в квадрат, тобто розв’язків стане знов чотири. Очевидно при 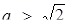 система розв’язків не має.
система розв’язків не має.
Відповідь: якщо 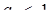 або
або 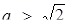 , то немає розв’язків; якщо
, то немає розв’язків; якщо 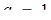 або
або 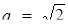 , то розв’язків чотири; якщо
, то розв’язків чотири; якщо 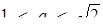 , то розв’язків вісім.
, то розв’язків вісім.
3. Знайти всі значення параметра а, при кожному з яких рівняння 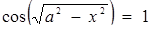 має рівно вісім розв’язків.
має рівно вісім розв’язків.
Розв’язання. Маємо 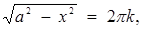 , де
, де  . Розглянемо функції
. Розглянемо функції 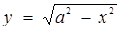 та
та 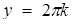 . Перша з них задає сім’ю гомотетичних півкіл з центром в О ( 0; 0), друга - сім’ю прямих, паралельних вісі абсцис.
. Перша з них задає сім’ю гомотетичних півкіл з центром в О ( 0; 0), друга - сім’ю прямих, паралельних вісі абсцис.
З рис.1.3.11 видно, що зі збільшенням радіуса 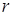 півкола зростає число коренів початкового рівняння. Їх буде рівно вісім, якщо
півкола зростає число коренів початкового рівняння. Їх буде рівно вісім, якщо 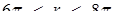 .
.
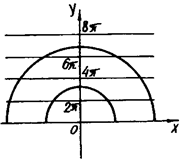
Рис.1.3.11
Зауважимо, що а не є радіусом півкола, т. як 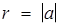 .
.
Відповідь: 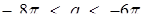 або
або 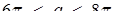 .
.
4. Знайти всі а, при яких системи рівносильні.
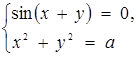 та
та 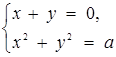
Розв’язання. Перепишемо першу систему в виді 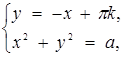 де
де 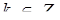
Перше рівняння системи задає сім’ю паралельних прямих, зображену на рис.1.3.12. Для випадку а > 0 друге рівняння системи задає сім’ю кіл.
Всі розв’язки другої з початкових систем містяться серед розв’язків першої.
Обернена вимога виконується лише тоді, коли кола 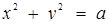 мають спільні точки тільки з прямою
мають спільні точки тільки з прямою 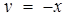 . Відстань між сусідніми прямими дорівнює
. Відстань між сусідніми прямими дорівнює 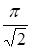 , тому для радіуса кола знаходимо обмеження
, тому для радіуса кола знаходимо обмеження 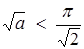 . Звідси
. Звідси 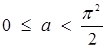 .
.
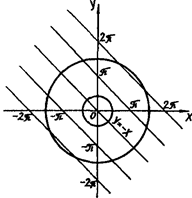
Рис.1.3.12
Оскільки ми розглядаємо випадок а > 0, то значення а = 0 потребує перевірки. Очевидно воно підходить. При а < 0 початкові системи розв’язків не мають, а значить, вони рівносильні.
Відповідь: 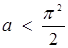 .
.
5. При яких додатних значеннях параметрів а та 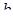 системи рівнянь
системи рівнянь
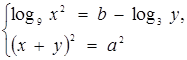 та
та 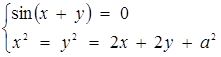
мають однакове число розв’язків?
Розв’язання. Друга система задає сім’ю паралельних прямих 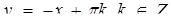 , та сім’ю гомотетичних кіл
, та сім’ю гомотетичних кіл 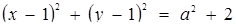 з центром О1 ( 1;
з центром О1 ( 1;
1) (рис.1.3.13). Оскільки за умовою 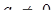 , то
, то 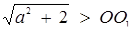 , і система має не менше чотирьох розв’язків. Очевидно такою ж властивістю володіє перша з початкових систем.
, і система має не менше чотирьох розв’язків. Очевидно такою ж властивістю володіє перша з початкових систем.
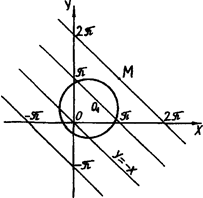
Рис.1.3.13
Вона рівносильна сукупності наступних двох систем:
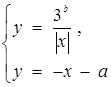 або
або 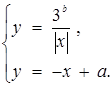
Оскільки а > 0, то сім’я паралельних прямих 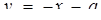 (рис.1.3.13) перетинає графік
(рис.1.3.13) перетинає графік 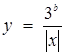 лише в одній точці, а значить, перша система сукупності має тільки один розв’язок. Друга система може мати не більше трьох розв’язків (рис.1.3.14). Тому ми вимагаємо від цієї системи мати рівно три розв’язки.
лише в одній точці, а значить, перша система сукупності має тільки один розв’язок. Друга система може мати не більше трьох розв’язків (рис.1.3.14). Тому ми вимагаємо від цієї системи мати рівно три розв’язки.
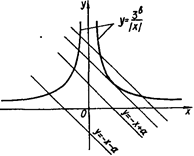
Рис.1.3.14
Остання умова досягається тоді, коли прямі 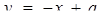 будуть перетинати криву
будуть перетинати криву 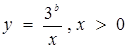 , в двох точках. Для цього необхідно і достатньо, щоб рівняння
, в двох точках. Для цього необхідно і достатньо, щоб рівняння 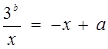 при а > 0 мало два кореня, тобто дискримінант квадратного рівняння
при а > 0 мало два кореня, тобто дискримінант квадратного рівняння 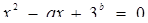 повинен бути додатним. Маємо
повинен бути додатним. Маємо 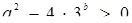 . Звідси для а > 0 знаходимо
. Звідси для а > 0 знаходимо 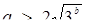
Тепер залишилося з’ясувати, при яких а друга з даних в умові систем має рівно чотири розв’язки. Розглянемо точку 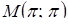 (рис.1.3.13). Якщо радіус кола буде більше або дорівнює О 1 М, то система очевидно буде мати більше чотирьох розв’язків. Тоді знаходимо
(рис.1.3.13). Якщо радіус кола буде більше або дорівнює О 1 М, то система очевидно буде мати більше чотирьох розв’язків. Тоді знаходимо 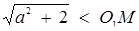 , тобто при а > 0 маємо
, тобто при а > 0 маємо 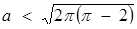 .
.
Тепер визначимо при яких 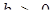
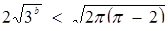 . Легко встановлюємо, що
. Легко встановлюємо, що 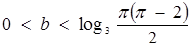 .
.
Відповідь: якщо 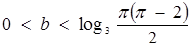 , то
, то 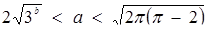 ; при інших b вимоги задачі не виконуються.
; при інших b вимоги задачі не виконуються.
Зауваження. При фіксованому 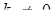 крива
крива 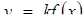 - результат стиску до вісі абсцис кривої
- результат стиску до вісі абсцис кривої 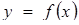 в
в 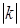 раз. (Іноді для випадку
раз. (Іноді для випадку 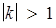 говорять, що крива розтягується від вісі)
говорять, що крива розтягується від вісі)
6. При кожному фіксованому значенні параметра а розв’язати рівняння 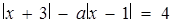 .
.
Розв’язання. Розглянемо функції 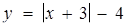 и
и 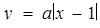 . На рис.1.3.15 побудовані графік першої з них, а також графіки шести представників сім’ї прямих
. На рис.1.3.15 побудовані графік першої з них, а також графіки шести представників сім’ї прямих 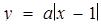 відповідно для випадків
відповідно для випадків 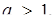
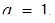
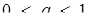
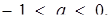
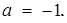
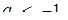 (Для а = 0 маємо вісь абсцис) Одержаний графічний образ дає повну інформацію про Розв’язання початкового рівняння. Залишилося лише знайти значення
(Для а = 0 маємо вісь абсцис) Одержаний графічний образ дає повну інформацію про Розв’язання початкового рівняння. Залишилося лише знайти значення 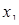 та
та 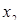 .
.
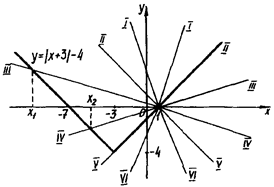
Рис.1.3.15
Очевидно шукані значення відповідно для  и
и 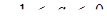 - це корені рівняння
- це корені рівняння 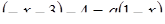 .
.
Звідси 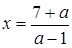 . При запису відповіді необхідно врахувати, що х = 1 - корінь початкового рівняння при будь-якому а.
. При запису відповіді необхідно врахувати, що х = 1 - корінь початкового рівняння при будь-якому а.
Відповідь: якщо 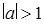 , то х = 1; якщо
, то х = 1; якщо 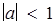 , то х = 1 або
, то х = 1 або 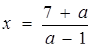 ;
;
якщо а = 1, то 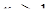 ; якщо а = - 1, то
; якщо а = - 1, то 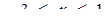 .
.
7. Знайти всі натуральні значення b, при кожному з яких вираз 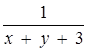 має зміст для всіх пар чисел (х; у), де
має зміст для всіх пар чисел (х; у), де 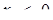 и
и 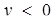 , для яких вираз
, для яких вираз 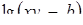 також має зміст.
також має зміст.
Розв’язання. Оскільки вирази 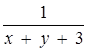 та
та 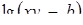 повинні мати зміст одночасно, то нескладно прийти до формулювання, рівносильного початковому: знайти всі натуральні b, при яких система має розв’язок:
повинні мати зміст одночасно, то нескладно прийти до формулювання, рівносильного початковому: знайти всі натуральні b, при яких система має розв’язок:
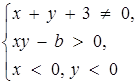
Графіком першої нерівності системи є всі точки координатної площини (х; у), окрім прямої 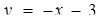 . Інші нерівності задають область, обмежену віткою гіперболи
. Інші нерівності задають область, обмежену віткою гіперболи 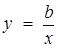 . (На рис.1.3.16 ця область показана штриховою лінією)
. (На рис.1.3.16 ця область показана штриховою лінією)
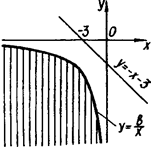
Рис.1.3.16
Система має розв’язки, якщо сім’я гіпербол 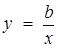 має не більше однієї спільної точки з прямою
має не більше однієї спільної точки з прямою 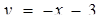 (одна точка відповідає моменту дотику). Для цього достатньо вимагати, щоб рівняння
(одна точка відповідає моменту дотику). Для цього достатньо вимагати, щоб рівняння 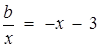 мало не більше одного кореня. Оскільки
мало не більше одного кореня. Оскільки 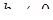 , то умова недодатності дискримінанта квадратного рівняння
, то умова недодатності дискримінанта квадратного рівняння 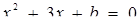 дає шукані значення параметра. Маємо
дає шукані значення параметра. Маємо 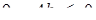 . І так як b - натуральне, знаходимо b= 3, 4,...
. І так як b - натуральне, знаходимо b= 3, 4,...
Відповідь: b= 3, 4,...
8. При яких значеннях а множина точок, задана нерівністю 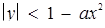 , є підмножиною множини точок, заданої нерівністю
, є підмножиною множини точок, заданої нерівністю 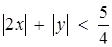 ?
?
Розв’язання. Графіком нерівності 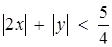 є область, обмежена ромбом (рис.1.3.17).
є область, обмежена ромбом (рис.1.3.17).
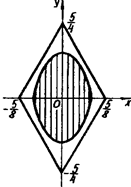
Рис.1.3.17
Нерівність 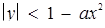 рівносильна системі
рівносильна системі 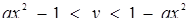 . Очевидно при
. Очевидно при 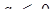 ця система задає необмежену множину точок (рис.1.3.18), яка не може поміститися в середині ромба. Якщо а > 0, то система задає фігуру, зображену на рис.1.3.19.
ця система задає необмежену множину точок (рис.1.3.18), яка не може поміститися в середині ромба. Якщо а > 0, то система задає фігуру, зображену на рис.1.3.19.
Задача зводиться до пошуку значень а, при яких ця фігура "стиснеться" до таких розмірів, що поміститься в ромб. Із міркувань симетрії для пошуку шуканих значень параметра достатньо вимагати від рівняння 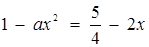 при
при 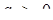 мати не більше одного кореня. Тоді
мати не більше одного кореня. Тоді 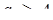 .
.
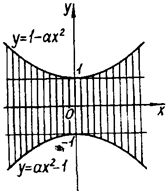
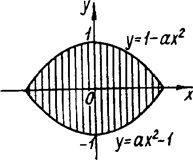
Рис.1.3.18 Рис.1.3.19
Відповідь: 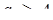 .
.
Дві прямі на площині
В основі ідеї розв’язку задач цього підрозділу лежить питання про дослідження взаємного розташування двох прямих: 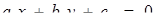 та
та 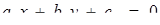 . Не будь-яке рівняння виду
. Не будь-яке рівняння виду 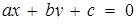 задає пряму: необхідно ще вимагати, щоб
задає пряму: необхідно ще вимагати, щоб 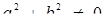 При дослідженні взаємного розташування двох прямих зручно спочатку розглянути випадки, коли коефіцієнти при у дорівнюють нулю (маємо вертикальне положення прямих), потім кожне з рівнянь представити у вигляді
При дослідженні взаємного розташування двох прямих зручно спочатку розглянути випадки, коли коефіцієнти при у дорівнюють нулю (маємо вертикальне положення прямих), потім кожне з рівнянь представити у вигляді 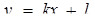
1. Знайти значення 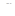 , при яких система рівнянь
, при яких система рівнянь
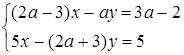
має єдиний розв’язок.
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при  задає вертикальну пряму
задає вертикальну пряму 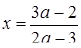 , яка перетинає графік другого рівняння, що рівносильно для системи мати єдиний розв’язок. Друге рівняння при
, яка перетинає графік другого рівняння, що рівносильно для системи мати єдиний розв’язок. Друге рівняння при 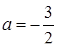 задає вертикальну пряму
задає вертикальну пряму  , яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо  та
та 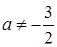 , то
, то 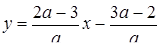 ,
, 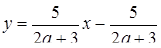 .
.
Прямі паралельні, якщо 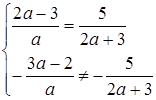 , звідки
, звідки 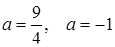
Прямі співпадають, якщо 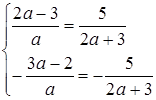 , звідки
, звідки 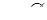
Прямі перетинаються, якщо 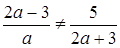 , звідки
, звідки 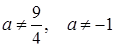 .
.
Відповідь: система має єдиний розв’язок при 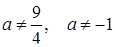 .
.
2. Покажіть, що система рівнянь
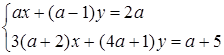
має єдиний розв’язок при всіх значеннях  .
.
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при  задає вертикальну пряму
задає вертикальну пряму  , яка перетинає графік другого рівняння, що рівносильне для системи мати єдиний розв’язок. Друге рівняння при
, яка перетинає графік другого рівняння, що рівносильне для системи мати єдиний розв’язок. Друге рівняння при 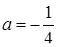 задає вертикальну пряму
задає вертикальну пряму 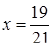 , яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинає графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо  , то
, то 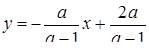 ; якщо
; якщо 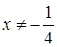 , то
, то 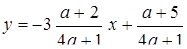 . Прямі паралельні, якщо
. Прямі паралельні, якщо 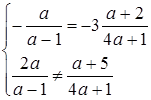 , звідки з першого рівняння
, звідки з першого рівняння 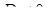 , розв’язків немає. Отже, співпадати прямі також не можуть.
, розв’язків немає. Отже, співпадати прямі також не можуть.
Відповідь: прямі перетинаються при всіх значеннях  .
.
3. Знайти всі значення  , при яких система рівнянь немає розв’язків:
, при яких система рівнянь немає розв’язків:
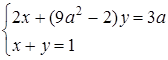
Розв’язання. Графіками рівнянь системи є прямі. Перше рівняння при 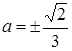 задає вертикальні прямі
задає вертикальні прямі 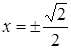 , які перетинають графік другого рівняння, що рівносильне для системи мати єдиний розв’язок.
, які перетинають графік другого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо 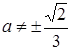 , то
, то 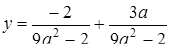 ;
; 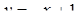 .
.
Система немає розв’язків, коли прямі паралельні, тобто
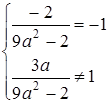
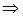
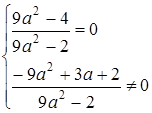
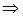
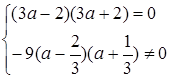
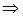
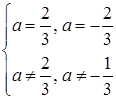
Відповідь: система немає розв’язків при 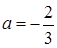 .
.
4. При яких значеннях  система рівнянь
система рівнянь
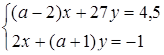
має нескінчену множину розв’язків?
Розв’язання. Графіками рівнянь системи є прямі. Друге рівняння при  задає вертикальну пряму
задає вертикальну пряму 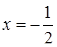 , яка перетинають графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
, яка перетинають графік першого рівняння, що рівносильне для системи мати єдиний розв’язок.
Якщо 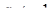 , то
, то 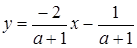 . З першого рівняння маємо
. З першого рівняння маємо 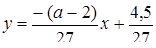 .
.
Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
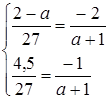
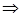
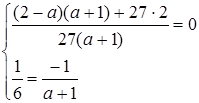
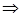
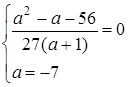
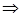
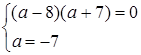
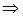

Відповідь: система має нескінчену множину розв’язків при  .
.
5. Знайти всі пари значень 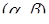 , при кожній з яких система рівнянь
, при кожній з яких система рівнянь
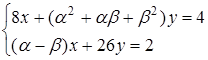
має нескінчену множину розв’язків.
Розв’язання. Перепишемо систему рівнянь у вигляді
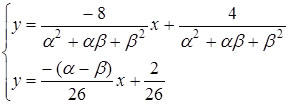
Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
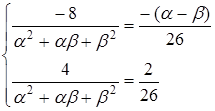
Помножуємо друге рівняння на 2 і додаємо до першого рівняння: 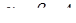 . Виражаємо
. Виражаємо 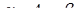 і підставляємо в друге рівняння:
і підставляємо в друге рівняння:
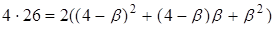
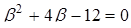
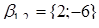 , тоді
, тоді 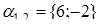
Відповідь: 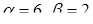 або
або 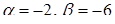 .
.
6. При яких значеннях 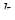 існують розв’язки системи рівнянь
існують розв’язки системи рівнянь
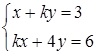 ,
,
які задовольняють одночасно нерівностям 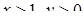 ?
?
Розв’язання. Знаходимо з першого рівняння 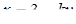 і підставляємо в друге рівняння:
і підставляємо в друге рівняння: 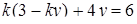 , звідки
, звідки 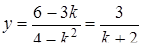 . За умовою задачі
. За умовою задачі 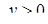 , тобто
, тобто 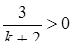 , звідки
, звідки  .
.
Тоді 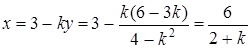 . За умовою задачі
. За умовою задачі 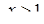 , тобто
, тобто 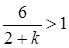 , звідки
, звідки 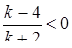 ,
, 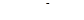 . Отже,
. Отже, 
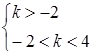
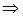
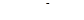 .
.
Відповідь: 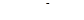 .
.
7. Знайти всі 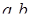 , при яких рівносильні системи рівнянь
, при яких рівносильні системи рівнянь
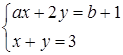 та
та 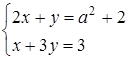 .
.
Розв’язання. Розглянемо другу систему: 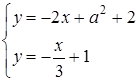 . Ця система має єдиний розв’язок при будь-яких
. Ця система має єдиний розв’язок при будь-яких 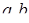 (
(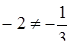 ). Для виконання умови рівноправності необхідно, щоб всі чотири прямі, які задаються рівняннями системи, мали спільну точку. Цю точку знайдено, розв’язавши систему
). Для виконання умови рівноправності необхідно, щоб всі чотири прямі, які задаються рівняннями системи, мали спільну точку. Цю точку знайдено, розв’язавши систему
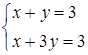
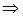
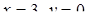 .
.
Підставимо знайдені значення 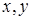 в перші рівняння заданих систем:
в перші рівняння заданих систем:
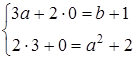
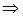
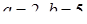 або
або 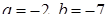 .
.
Перша система при 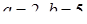 має нескінчено багато розв’язків:
має нескінчено багато розв’язків:
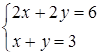 .
.
Тому системи рівнянь рівносильні при 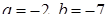 .
.
Відповідь: 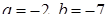 .
.
8. Числа 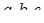 такі, що система рівнянь
такі, що система рівнянь
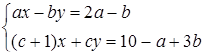
має нескінчено багато розв’язків, причому 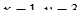 - один із цих розв’язків. Знайти числа
- один із цих розв’язків. Знайти числа 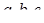 .
.
Розв’язання. Перепишемо систему у вигляді:
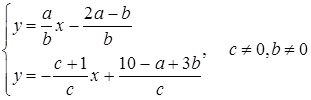 .
.
Система має нескінчену множину розв’язків, коли прямі співпадають, тобто
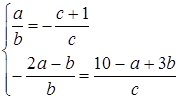
Так як 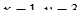 - один із цих розв’язків системи, то підставимо його в систему:
- один із цих розв’язків системи, то підставимо його в систему:
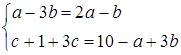
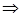
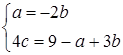
Тоді
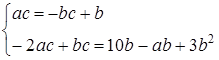
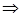
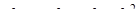 .
.
З системи трьох рівнянь знаходимо
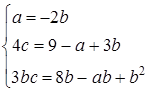
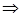
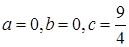 або
або 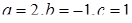 .
.
Відповідь: 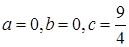 або
або 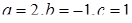 .
.
9. Знайти всі значення  , при кожному з яких для будь-якого значення
, при кожному з яких для будь-якого значення 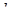 система
система
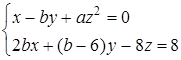
мала б хоча б один розв’язок 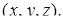
Розв’язання. Розглянемо задану систему як систему з двома невідомими 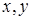 та трьома параметрами
та трьома параметрами 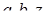 Якщо
Якщо  та
та  перепишемо задану систему таким чином:
перепишемо задану систему таким чином:
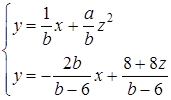
З цієї системи маємо: система має розв’язки, якщо 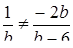 , тобто
, тобто 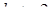 та
та 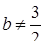 при будь-яких значеннях
при будь-яких значеннях 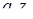
При  перше рівняння визначає вертикальну пряму, друге - невертикальну. Таким чином, при
перше рівняння визначає вертикальну пряму, друге - невертикальну. Таким чином, при  система має розв’язок для будь-яких
система має розв’язок для будь-яких 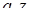 Аналогічно для
Аналогічно для  .
.
Необхідно дослідити систему при  та
та 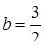 . При даних значеннях рівняння системи задають або паралельні або співпадаючі прямі. Випадку перетину прямих відповідає рівняння:
. При даних значеннях рівняння системи задають або паралельні або співпадаючі прямі. Випадку перетину прямих відповідає рівняння: 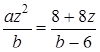
При  маємо
маємо 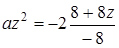 ,
, 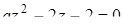 ,
, 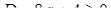 ,
, 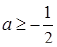 . При
. При 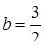 маємо
маємо 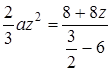 ,
, 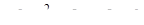 ,
, 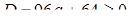 ,
, 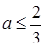 . Таким чином,
. Таким чином, 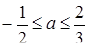 . Відповідь:
. Відповідь: 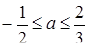 .
.
10. Знайти  такі, щоб при будь-яких
такі, щоб при будь-яких  система рівнянь мала б хоча б один розв’язок:
система рівнянь мала б хоча б один розв’язок: 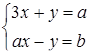
Розв’язання. Перепишемо систему рівнянь у вигляді: 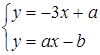 . При
. При 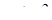 задана система має єдиний розв’язок при будь-яких значеннях
задана система має єдиний розв’язок при будь-яких значеннях 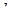 . Тому достатньо знайти такі
. Тому достатньо знайти такі 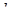 , щоб система мала б розв’язок при
, щоб система мала б розв’язок при  .
.
Маємо 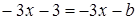 , звідси
, звідси 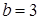 .
.
Відповідь: 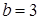
Задачі для самостійної роботи
1. Визначити число розв’язків системи в залежності від значень параметра а.
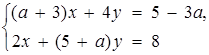
Розв’язання. Графіками рівнянь системи є прямі. Оскільки коефіцієнт при у в першому рівнянні не дорівнює нулю, то це рівняння задає невертикальну пряму 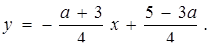 Друге рівняння при
Друге рівняння при  задає вертикальну пряму, яка очевидно перетинає графік першого рівняння, що рівносильне початковій системі мати єдиний розв’язок. Якщо
задає вертикальну пряму, яка очевидно перетинає графік першого рівняння, що рівносильне початковій системі мати єдиний розв’язок. Якщо 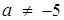 , то маємо
, то маємо 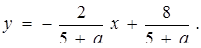 Прямі паралельні, якщо
Прямі паралельні, якщо 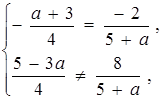
Прямі співпадають, якщо 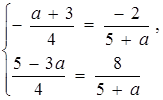
Прямі перетинаються, якщо 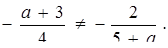
Розв’язання першої системи  другої:
другої: 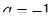 Розв’язання останньої нерівності
Розв’язання останньої нерівності 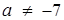 и
и 
Відповідь: якщо 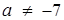 та
та  то система має єдиний Розв’язання (зазначимо, що значення
то система має єдиний Розв’язання (зазначимо, що значення  враховано); якщо
враховано); якщо  то розв’язків нескінчене багато; якщо
то розв’язків нескінчене багато; якщо  то розв’язків немає.
то розв’язків немає.
Зауваження. Розглянута система належить класу систем двох лінійних рівнянь с двома змінними х та у, тобто систем виду
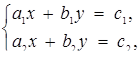
де 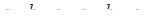 - деякі числа (параметри).
- деякі числа (параметри).
2. Задані два твердження: а) система 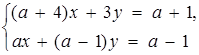 має нескінченно багато розв’язків; б) прямі, задані рівняннями
має нескінченно багато розв’язків; б) прямі, задані рівняннями 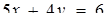 та
та 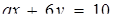
перетинаються в другій чверті декартової прямокутної системи координат. При яких значеннях а одне з тверджень істинно, а інше - хибне?
Розв’язання. Графіком першого рівняння системи є невертикальна пряма 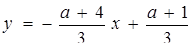 . При
. При  система очевидно має єдиний Розв’язання (друге рівняння задає вертикальну прямую). Якщо
система очевидно має єдиний Розв’язання (друге рівняння задає вертикальну прямую). Якщо  , то маємо
, то маємо 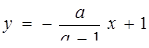 . Звідси система має нескінченно багато розв’язків, якщо
. Звідси система має нескінченно багато розв’язків, якщо
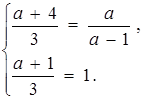
Знаходимо  .
.
Прямі, задані в твердженні б), зручно записати так:
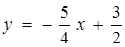 та
та 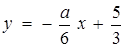 . Зрозуміло, що вони будуть перетинатися, якщо
. Зрозуміло, що вони будуть перетинатися, якщо
 2020-01-14
2020-01-14 259
259








