Погляд на параметр як на рівноправну змінну знаходить своє відображення в графічних методах. Оскільки параметр "рівний в правах" зі змінною, то йому, природно, можна "виділити" і свою координатну вісь. Таким чином виникає координатна площина 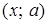 .
.
Відмова від традиційного вибору букв х та у для позначення осей, визначає один з ефективніших методів розв’язку задач з параметрами.
Для того, щоб найбільш повно розкрити можливості цього метода, покажемо його застосування для розв’язування основних типів задач з параметрами.
Дамо самі загальні признаки, які, можливо, допоможуть впізнавати задачі, які підходять під цей метод: в задачі фігурують лише один параметр а та одна змінна х, вони конструюють деякі аналітичні вирази F 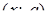 , G
, G 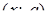 і т.д.; графіки рівнянь F
і т.д.; графіки рівнянь F 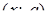 = 0, G
= 0, G 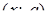 = 0 і т.д. в системі координат
= 0 і т.д. в системі координат 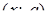 будуються нескладно.
будуються нескладно.
Сам процес розв’язування схематично виглядає так.
Спочатку будується графічний образ, потім, перетинаючи отриманий графік прямими, перпендикулярними параметричній вісі, "знімаємо" потрібну інформацію.
1. Знайти всі значення параметра  , при яких система нерівностей
, при яких система нерівностей
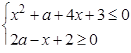
задовольняється лише при одному 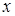 .
.
Розв’язання. Перепишемо систему в такому виді:
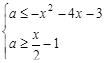
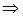
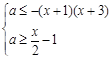
Всі розв’язки цієї системи утворюють область, показану на рисунку штриховою лінією.
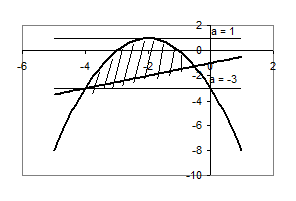
Рис.2.1
Вимога єдності розв’язку даної системи: горизонтальні прямі повинні мати з цією областю тільки одну спільну точку.
Знаходимо точки перетину графіків: 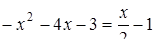 , звідки
, звідки 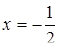 ,
,  . Тоді
. Тоді 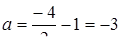 та
та 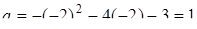 .
.
Лише прямі  та
та 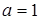 задовольняють вимозі єдності розв’язку системи.
задовольняють вимозі єдності розв’язку системи.
Відповідь:  та
та 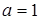 .
.
2. Знайти всі значення параметра  , при яких система нерівностей
, при яких система нерівностей
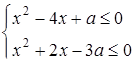
задовольняється лише при одному 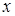 .
.
Розв’язання. Перепишемо систему в такому виді:
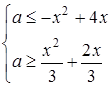 .
.
Всі розв’язки цієї системи утворюють область, показану на рисунку штриховою лінією.
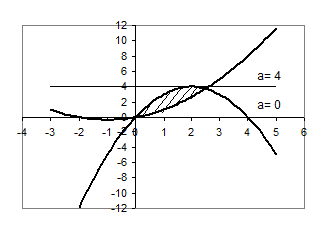
Рис.2.2
Вимога єдності розв’язку даної системи: горизонтальні прямі повинні мати з цією областю тільки одну спільну точку.
Знаходимо точки перетину графіків: 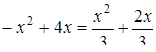 , звідки
, звідки 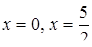 .
.
З рисунка видно, що лише прямі 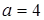 та
та 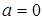 задовольняють вимозі єдності розв’язку системи.
задовольняють вимозі єдності розв’язку системи.
Відповідь: 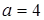 та
та 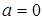 .
.
3. При яких значеннях  рівняння
рівняння 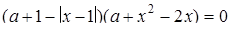 має рівно три кореня?
має рівно три кореня?
Розв’язання. Маємо
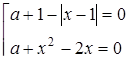
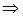
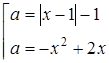
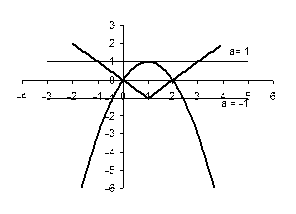
Рис.2.3
Графік цієї сукупності - об’єднання “кута" та параболи.
Лише прямі 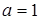 та
та  перетинають знайдене об’єднання в трьох точках.
перетинають знайдене об’єднання в трьох точках.
Відповідь: 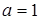 та
та  .
.
4. При яких значеннях  рівняння
рівняння 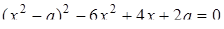 має рівно три розв’язки?
має рівно три розв’язки?
Розв’язання. Розв’яжемо задане рівняння як квадратне відносно  :
:
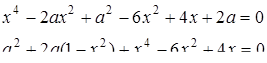
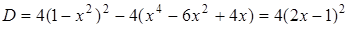
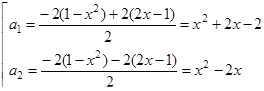
Графік цієї сукупності - об’єднання двох парабол.
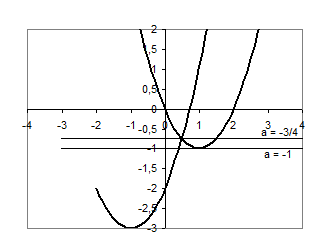
Рис.2.4
Знайдемо точки перетину графіків функцій:  , звідки
, звідки 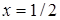 .
.
 та
та  ,
, 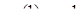 .
.
Лише прямі 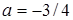 та
та  перетинають знайдене об’єднання в трьох точках.
перетинають знайдене об’єднання в трьох точках.
Відповідь: 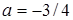 та
та  .
.
5. В залежності від параметра  визначити число коренів рівняння
визначити число коренів рівняння
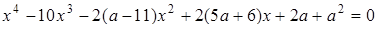
Розв’язання. Розв’яжемо задане рівняння як квадратне відносно  :
:
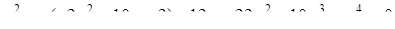

Графік цієї сукупності - об’єднання двох парабол.
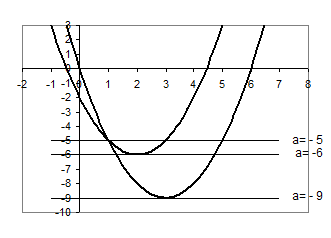
Рис.2.5
Знайдемо координати вершин кожної з парабол:
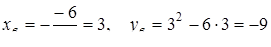 та
та
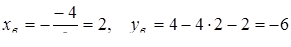 .
.
Знайдемо також точки перетину графіків функцій:  , звідки
, звідки 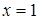 , тоді
, тоді 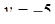 .
.
Відповідь: якщо  , то розв’язків немає; якщо
, то розв’язків немає; якщо  , то 1 розв’язок;
, то 1 розв’язок;
якщо  , то 2 розв’язки; якщо
, то 2 розв’язки; якщо  або
або  , то 3 розв’язки;
, то 3 розв’язки;
якщо  або
або  , то 4 розв’язки.
, то 4 розв’язки.
6. Знайти всі дійсні значення  , для кожного з яких рівняння
, для кожного з яких рівняння
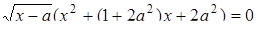
має тільки два різних коренів. Записати ці корені.
Розв’язання. Перепишемо рівняння у вигляді сукупності:
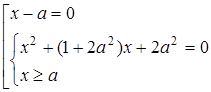
Розв’язками системи є 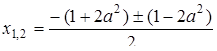 , звідки
, звідки  ,
,  ,
, 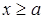 .
.
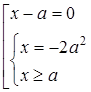 та
та 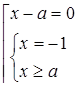
Відповідь: якщо  , то
, то 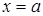 або
або  ;
;
якщо 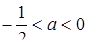 , то
, то 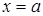 або
або  .
.
7. Знайти всі числа 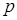 , при яких існує єдине число
, при яких існує єдине число 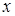 , яке задовольняє одночасно наступним умовам:
, яке задовольняє одночасно наступним умовам: 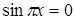 та
та 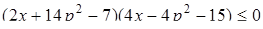 .
.
Розв’язання. Перепишемо систему в вигляді:
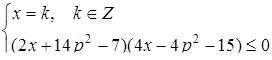

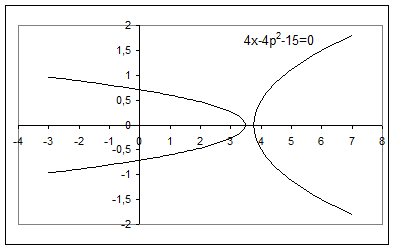
Рис.2.6
На координатній площині 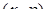 перше рівняння задає сім’ю вертикальних прямих. Параболи
перше рівняння задає сім’ю вертикальних прямих. Параболи 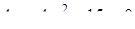 та
та 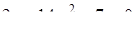 розбивають площину на 3 частини. Заштрихована область є розв’язком нерівності системи. Це точки, в яких дотичні будуть горизонтальними:
розбивають площину на 3 частини. Заштрихована область є розв’язком нерівності системи. Це точки, в яких дотичні будуть горизонтальними:
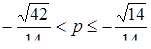 або
або 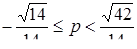 .
.
Відповідь: 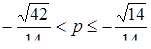 або
або 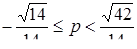 .
.
Задачі для самостійної роботи
1. При яких значеннях а рівняння 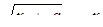 має два кореня?
має два кореня?
Розв’язок. Переходимо до рівносильної системи
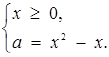
Ця система на координатній площині 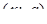 задає криву, наведену на рис.2.7 неперервною лінією. Всі точки цієї дуги параболи (і тільки вони) мають координати
задає криву, наведену на рис.2.7 неперервною лінією. Всі точки цієї дуги параболи (і тільки вони) мають координати 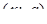 , які задовольняють початковому рівнянню. Тому число розв’язків рівняння при кожному фіксованому значенні параметра а дорівнює кількості точок перетину кривої з горизонтальною прямою, яка відповідає цьому значенню параметра. Очевидно при
, які задовольняють початковому рівнянню. Тому число розв’язків рівняння при кожному фіксованому значенні параметра а дорівнює кількості точок перетину кривої з горизонтальною прямою, яка відповідає цьому значенню параметра. Очевидно при 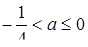 прямі перетинають графік в двох точках, що рівносильне для початкового рівняння мати два кореня.
прямі перетинають графік в двох точках, що рівносильне для початкового рівняння мати два кореня.
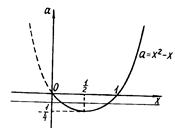
Рис.2.7
Відповідь: 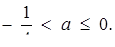
2. Знайти всі значення а, при яких система має єдиний розв’язок.
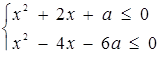
Розв’язок. Перепишемо початкову систему в такому вигляді:
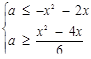
Все розв’язки цієї системи (пари виду 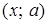 ) утворюють область, наведену на рис.2.8 штриховою лінією.
) утворюють область, наведену на рис.2.8 штриховою лінією.
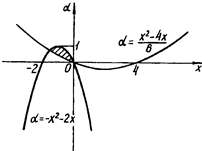
Рис.2.8
Вимога єдності розв’язка даної системи така: горизонтальні прямі повинні мати зі знайденою областю тільки одну спільну точку. Лише прямі а = 0 та а = 1 задовольняють висунутій вимозі.
Відповідь: а = 0 або а = 1.
3. При яких значеннях а рівняння 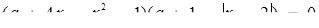 має
має
рівно три кореня?
Розв’язок. Маємо
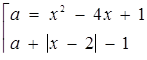
Графік цієї сукупності - об’єднання "кута" та параболи (рис.2.9).
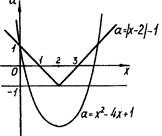
Рис.2.9
Лише пряма 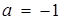 перетинає знайдене об’єднання в трьох точках.
перетинає знайдене об’єднання в трьох точках.
Відповідь: 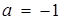
4. Скільки розв’язків має система в залежності від значень параметра с?
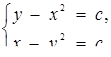
Розв’язок. Перепишемо систему у вигляді
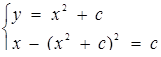
Кількість коренів другого рівняння системи дорівнює числу розв’язків самої системи. Маємо 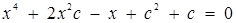 . Розглянувши це рівняння як квадратне відносно с, одержимо наступну сукупність.
. Розглянувши це рівняння як квадратне відносно с, одержимо наступну сукупність.
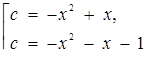
На рис.2.10 наведено сукупність рівнянь на координатній площині  .
.
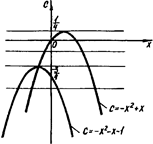
Рис.2.10
Координати точок перетину парабол можна знайти, розв’язавши рівняння  . Звідси
. Звідси 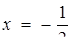 . Для запису відповіді залишилося лише зазначити, що спільна точка цих парабол - вершина параболи
. Для запису відповіді залишилося лише зазначити, що спільна точка цих парабол - вершина параболи 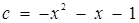 .
.
Відповідь: якщо 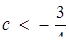 , то розв’язків чотири; якщо
, то розв’язків чотири; якщо 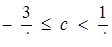 , то
, то
розв’язків два; якщо 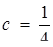 , то розв’язок один; якщо
, то розв’язок один; якщо 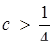 , то розв’язків немає.
, то розв’язків немає.
5. Знайти всі значення параметра b, при яких рівняння 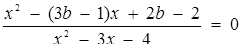 має один розв’язок.
має один розв’язок.
Розв’язок. Задане рівняння рівносильне системі
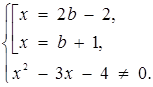
За допомогою цієї системи будуємо графік початкового рівняння (рис.2.11).
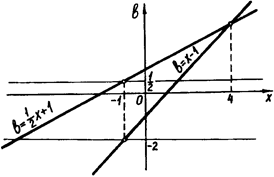
Рис.2.11
Саме наявність "проколов" в цьому графіку дозволяє при 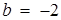 та
та 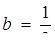 мати рівнянню єдиний розв’язок.
мати рівнянню єдиний розв’язок.
Відповідь: 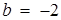 або
або 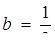
6. При яких значеннях параметра а рівняння 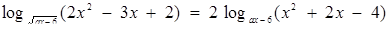 має єдиний розв’язок?
має єдиний розв’язок?
Розв’язок. Запишемо систему, рівносильну початковому рівнянню:
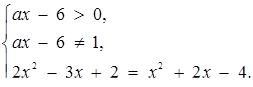 , Звідси знайдемо
, Звідси знайдемо
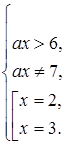
Перші дві нерівності системи задають множину точок, наведену на рис.2.12 штриховою лінією, причому в цю множину не входять гіперболи ах = 7 та ах = 6.
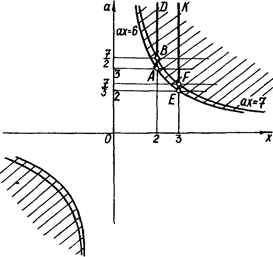
Рис.2.12
Тоді відрізок АВ та промінь BD, відрізок EF та промінь FK, які лежать відповідно на прямих  та
та 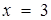 , є графіком початкового рівняння. Далі залишилося лише "зняти" з картинки:
, є графіком початкового рівняння. Далі залишилося лише "зняти" з картинки: 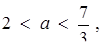 або
або 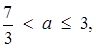 або
або 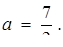
Відповідь: 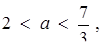 або
або 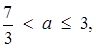 або
або 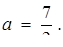
7. Знайти всі значення параметра а, при яких рівняння  має рівно два різних розв’язки.
має рівно два різних розв’язки.
Розв’язок. Задане рівняння рівносильне сукупності двох систем:
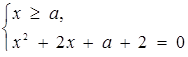 або
або 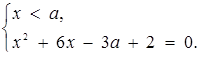 Звідси
Звідси
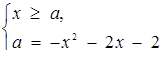 або
або 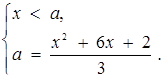
При побудови графіка початкового рівняння важливо врахувати, що параболи 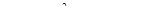
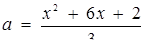 та пряма
та пряма 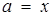 мають дві спільні точки: А (-2; - 2), В (-1; - 1), причому точка В - вершина першої з записаних парабол. Вершина другої параболи
мають дві спільні точки: А (-2; - 2), В (-1; - 1), причому точка В - вершина першої з записаних парабол. Вершина другої параболи 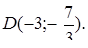
Графік початкового рівняння наведено на рис.2.13.
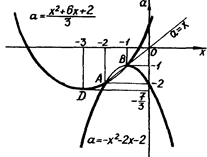
Рис.2.13
Звідси знаходимо 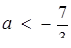 або
або 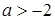 . Відповідь:
. Відповідь: 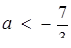 або
або 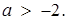 .
.
8. Знайти множину всіх чисел а, для кожного з яких рівняння  має тільки два різних кореня.
має тільки два різних кореня.
Розв’язок. Перепишемо задане рівняння в наступному виді: 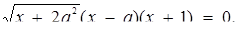 Тепер важливо не втратите, що
Тепер важливо не втратите, що 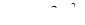
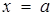 та
та 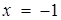 - корені початкового рівняння лише при умові
- корені початкового рівняння лише при умові  Графік заданого рівняння зручно будувати, відводячи змінній х вісь ординат. На рис.2.14 шуканий графік - об’єднання неперервних ліній.
Графік заданого рівняння зручно будувати, відводячи змінній х вісь ординат. На рис.2.14 шуканий графік - об’єднання неперервних ліній.
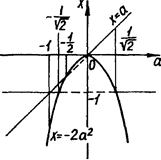
Рис.2.14
Відповідь "зчитується" вертикальними прямими: 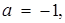 або
або 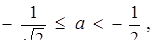 або
або 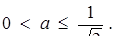
Відповідь: 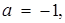 або
або 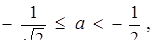 або
або 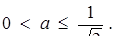
9. Знайти всі невід’ємні числа 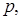 при яких існує єдине число
при яких існує єдине число 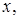 яке задовольняє системі
яке задовольняє системі
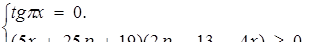
Розв’язок. Маємо
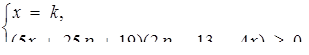 де
де 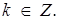
Перше рівняння на координатній площині 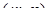 задає сім’ю вертикальних прямих (рис.2.15). Прямі
задає сім’ю вертикальних прямих (рис.2.15). Прямі  та
та  розбивають площину на чотири області. Деякі з них є розв’язками нерівності системи. Для того, щоб встановити які - можна взяти з кожної області по пробній точці. Та область, точка якої задовольняє нерівності, є її розв’язком. Для заданої нерівності розв’язком будуть дві області, обмежені кутами АМВ та DMC. Оскільки за умовою
розбивають площину на чотири області. Деякі з них є розв’язками нерівності системи. Для того, щоб встановити які - можна взяти з кожної області по пробній точці. Та область, точка якої задовольняє нерівності, є її розв’язком. Для заданої нерівності розв’язком будуть дві області, обмежені кутами АМВ та DMC. Оскільки за умовою 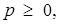 то для розв’язку задачі достатньо обмежитися множиною, відміченою штриховою лінією на рис.2.15.
то для розв’язку задачі достатньо обмежитися множиною, відміченою штриховою лінією на рис.2.15.
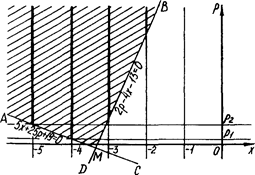
Рис.2.15
Тоді початковій системі задовольняють всі точки (і тільки вони), які лежать на променях і виділені на графіку жирними лініями.
При фіксованому 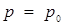 число розв’язків початкової системи дорівнює кількості точок перетину горизонтальної прямої
число розв’язків початкової системи дорівнює кількості точок перетину горизонтальної прямої 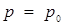 з відміченими променями. По рисунку видно, що вимога єдиності розв’язку досягається, якщо
з відміченими променями. По рисунку видно, що вимога єдиності розв’язку досягається, якщо 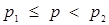 , де
, де  та
та  - відповідно ординати точок перетину двох пар прямих
- відповідно ординати точок перетину двох пар прямих 
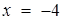 та
та 
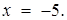 Звідси
Звідси 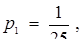
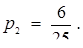
Відповідь: 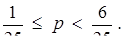
10. Для яких а в множині розв’язків нерівності 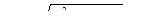 міститься проміжок
міститься проміжок 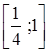 ?
?
Розв’язок. Запишемо сукупність двох систем, рівносильну початковому рівнянню:
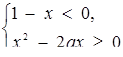 або
або 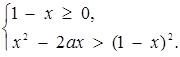
Оскільки в розв’язок першої системи ні при яких значеннях параметра а не може входити відрізок 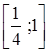 , то необхідні дослідження проведемо для другої системи. Маємо
, то необхідні дослідження проведемо для другої системи. Маємо
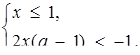
Позначимо 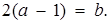 Тоді друга нерівність системи на координатній площині
Тоді друга нерівність системи на координатній площині 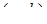 задає множину, наведену на рис.2.16 штриховою лінією.
задає множину, наведену на рис.2.16 штриховою лінією.
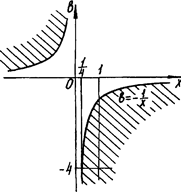
Рис.2.16
Тепер за допомогою рисунка легко встановити, що при 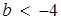 в знайденій множині містяться всі точки, абсциси яких пробігають всі значення з проміжку
в знайденій множині містяться всі точки, абсциси яких пробігають всі значення з проміжку 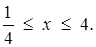 Тоді
Тоді 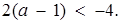 Звідси
Звідси 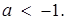
Відповідь: 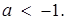
11. При яких значеннях параметра а система
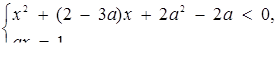
має розв’язки?
Розв’язок. Маємо
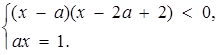
Нерівність системи задає область, обмежену кутами АКБ и CKD ( рис.2.17).
. 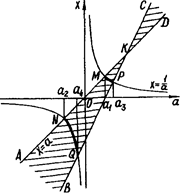
Рис.2.17
Тоді абсциси виділених дуг гіперболи 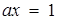 - розв’язки початкової системи. Знайдемо абсциси точок
- розв’язки початкової системи. Знайдемо абсциси точок 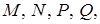 розв’язавши рівняння
розв’язавши рівняння 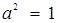 та
та 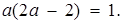 Звідси для перелічених точок абсциси відповідно дорівнюють
Звідси для перелічених точок абсциси відповідно дорівнюють 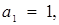

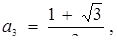
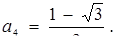 Залишилося записати
Залишилося записати 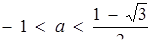 або
або 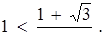
Відповідь: 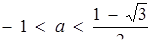 або
або 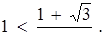
12. Знайти всі значення а, при яких будь-який розв’язок нерівності 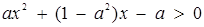 по модулю, не перевищує двох.
по модулю, не перевищує двох.
Розв’язок. Перепишемо задану нерівність в такому виді:

Графіки рівнянь 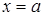 и
и 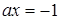 розбивають координатну площину
розбивають координатну площину  на чотири області. "Методом інтервалів" встановлюємо, що розв’язком початкової нерівності будуть заштриховані області (рис.2.18).
на чотири області. "Методом інтервалів" встановлюємо, що розв’язком початкової нерівності будуть заштриховані області (рис.2.18).
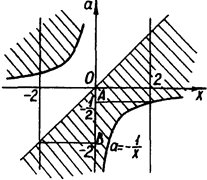
Рис.2.18
Тепер, якщо при деякому фіксованому значенні  пряма
пряма 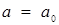 в перетині зі знайденою областю дає лише точки, абсциси яких задовольняють умові
в перетині зі знайденою областю дає лише точки, абсциси яких задовольняють умові  то
то  - одне з шуканих значень параметра. Тоді очевидно, що всі а з відрізка АВ складаються
- одне з шуканих значень параметра. Тоді очевидно, що всі а з відрізка АВ складаються 
Відповідь: 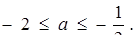
13. При яких значеннях а множина розв’язків нерівності 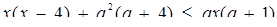 містить не більше чотирьох цілих значень
містить не більше чотирьох цілих значень 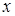 ?
?
Розв’язок. Раніше встановлено, що задана нерівність рівносильна сукупності двох систем:
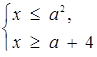 або
або 
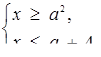
За допомогою цієї сукупності наведено розв’язки початкової нерівності на рис.2.19.
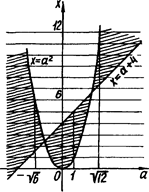
Рис.2.19
Проведемо прямі 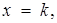 де
де 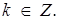 Тоді значення
Тоді значення 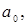 для якого пряма
для якого пряма 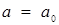 перетинає прямі
перетинає прямі 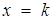 не більш, ніж в чотирьох точках з відміченої множини, буде шуканим. Проводячи аналіз графіка, приходимо до висновку, що в заданій задачі
не більш, ніж в чотирьох точках з відміченої множини, буде шуканим. Проводячи аналіз графіка, приходимо до висновку, що в заданій задачі  або
або  або
або 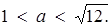
Відповідь:  або
або  або
або 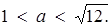
14. Розв’язати нерівність  .
.
Розв’язок. Наступна сукупність двох систем рівносильна заданій нерівності:
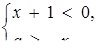 або
або 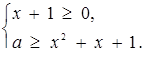
Далі, при об’єднанні графічних образів кожної з цих систем необхідно врахувати, що пряма 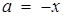 дотикається параболи
дотикається параболи 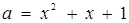 в точці (-1;1).
в точці (-1;1).
На рис.2.20 наведено всі розв’язки початкової нерівності.
Горизонтальні прямі, які перетинають цю множину, перетинають її по відрізку (за виключенням однієї прямої 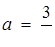 ). Очевидно абсциси всіх точок цього відрізка і будуть розв’язками заданої нерівності.
). Очевидно абсциси всіх точок цього відрізка і будуть розв’язками заданої нерівності.
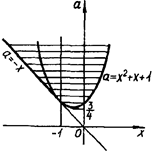
Рис.2.20
Для одержання відповіді залишилося виразити х через а в рівнянні 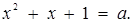 При
При 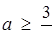 маємо
маємо 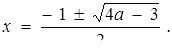
Відповідь: при 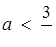 розв’язків не має; при
розв’язків не має; при 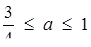
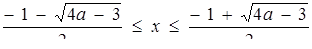 ; при
; при 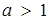 , розв’язком буде відрізок
, розв’язком буде відрізок  , де
, де 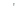 - більший з коренів
- більший з коренів  та
та  .
.
15. Розв’язати нерівність 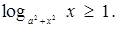
Розв’язок. Задана нерівність рівносильна сукупності двох систем:
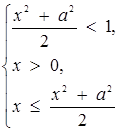 або
або 
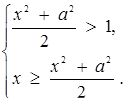 Звідси
Звідси
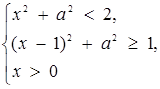 або
або 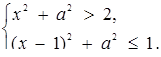
На координатній площині  перша система задає множину точок першого та четвертого координатних кутів, які одночасно лежать всередині кола з центром (0; 0) і радіуса
перша система задає множину точок першого та четвертого координатних кутів, які одночасно лежать всередині кола з центром (0; 0) і радіуса 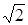 та поза колом з центром (1; 0) і радіуса 1. Друга система - множина точок, які одночасно лежать поза першим колом, але знаходяться в другому колі. Тоді всі розв’язки початкової нерівності наведено на рис.2.21.
та поза колом з центром (1; 0) і радіуса 1. Друга система - множина точок, які одночасно лежать поза першим колом, але знаходяться в другому колі. Тоді всі розв’язки початкової нерівності наведено на рис.2.21.
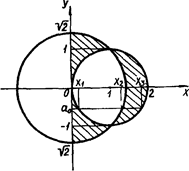
Рис.2.21
Зазначимо, що, наприклад, пряма 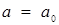 (см. рисунок) перетинає кола в точках з абсцисами
(см. рисунок) перетинає кола в точках з абсцисами 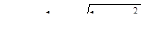
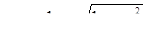 Тепер нескладно "прочитати" з рисунка відповідь.
Тепер нескладно "прочитати" з рисунка відповідь.
Відповідь: Якщо  то
то 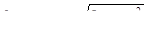 якщо
якщо  то
то 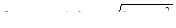 або
або  якщо
якщо 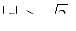 то немає розв’язків.
то немає розв’язків.
Наприкінці, розглянемо технологію складання задач. Розглянемо задачу.
Навести на координатній площині 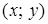 розв’язок системи нерівностей
розв’язок системи нерівностей
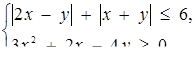
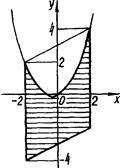
Рис.2.22
На рис.2.22 наведено цей розв’язок (область зі штриховою лінією).
Тепер, замінивши у на а, за допомогою графічного образу легко скласти наступні задачі.
При яких значеннях параметра а система нерівностей
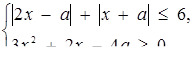
1) має розв’язок? 2) має єдиний розв’язок? 3) має тільки від’ємні розв’язки? 4) має тільки додатні розв’язки? 5) має тільки розв’язки, які задовольняють умові 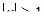 ;
;
6) має хоча б один розв’язок, якій задовольняє умові 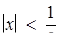 ? 7) має розв’язок, який містить відрізок
? 7) має розв’язок, який містить відрізок 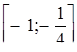 ? 8) має розв’язки, які містять не більше трьох цілих чисел?
? 8) має розв’язки, які містять не більше трьох цілих чисел?
 2020-01-14
2020-01-14 158
158








