В цьому параграфі наведені задачі, для розв’язання яких використовуються наглядно-графічні міркування, причому при побудові необхідного графічного образу використовується апарат похідної.
1. Скільки розв’язків в залежності від параметра  має рівняння
має рівняння 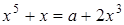 ?
?
Розв’язання. Перепишемо рівняння у вигляді:  . Маємо
. Маємо
 ,
,  ,
,  ,
,  , звідки
, звідки 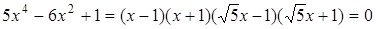 . Отже,
. Отже,
| x | (-¥, - 1) | -1 | (-1; - 1/Ö5) | -1/Ö5 | (-1/Ö5; 1/Ö5) | 1/Ö5 | (1/Ö5; 1) | 1 | (1; +¥) |
| a/ (x) | + | 0 | - | 0 | + | 0 | - | 0 | + |
| a (x) | | 0 | ¯ | -16Ö5/125 | | -16Ö5/125 | ¯ | 0 | |
Побудуємо графік функції  .
.

Рис.3.1
Якщо 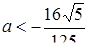 або
або  , то рівняння має 1 розв’язок (положення І та ІV); якщо
, то рівняння має 1 розв’язок (положення І та ІV); якщо  (положення ІІ та ІІІ), то рівняння має 2 розв’язки; якщо
(положення ІІ та ІІІ), то рівняння має 2 розв’язки; якщо 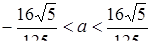 , то рівняння має 3 розв’язки (між положеннями ІІ та ІІІ). Відповідь: якщо
, то рівняння має 3 розв’язки (між положеннями ІІ та ІІІ). Відповідь: якщо 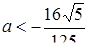 або
або  , то 1 розв’язок; якщо
, то 1 розв’язок; якщо  , то 2 розв’язки; якщо
, то 2 розв’язки; якщо 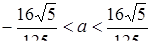 , то 3 розв’язки.
, то 3 розв’язки.
2. При яких  рівняння
рівняння  має три розв’язки? Розв’язання. Перепишемо рівняння у вигляді:
має три розв’язки? Розв’язання. Перепишемо рівняння у вигляді: 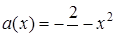 ,
,  . Знаходимо похідну:
. Знаходимо похідну: 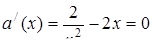 , звідки
, звідки  . Отже,
. Отже,
| x | (-¥, 0) | (0;1) | 1 | (1; +¥) |
| a/ (x) | + | + | 0 | - |
| a (x) | | | -3 | ¯ |
Побудуємо графік функції 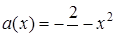 .
.
Рис.3.2
Ті значення  , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже,
, для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже,  .
.
Відповідь:  .
.
3. При яких  рівняння
рівняння 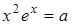 має три розв’язки?
має три розв’язки?
Розв’язання. Перепишемо рівняння у вигляді:  . Знаходимо похідну:
. Знаходимо похідну:
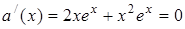 , звідки
, звідки  ,
, 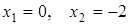 . Отже,
. Отже,
| x | (-¥, - 2) | -2 | (-2; 0) | 0 | (0; +¥) |
| a/ (x) | + | 0 | - | 0 | + |
| a (x) | | 4/e2 | ¯ | 0 | |
Побудуємо графік функції  .
.

Рис.3.3
Ті значення  , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже,
, для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. Отже,  .
.
Відповідь:  .
.
4. Скільки розв’язків має рівняння  на проміжку
на проміжку  ?
?
Розв’язання. Перепишемо рівняння у вигляді: 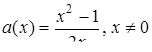 . Знаходимо похідну:
. Знаходимо похідну:  . Побудуємо графік функції
. Побудуємо графік функції 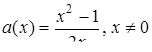 .
.
Знайдемо значення функції в граничних точках проміжку  :
:
 ,
,  .
.

Рис.3.4
З рис.3.4 випливає, що при 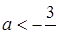 або
або  рівняння має 1 розв’язок; при
рівняння має 1 розв’язок; при  рівняння має 2 розв’язки.
рівняння має 2 розв’язки.
Відповідь: якщо 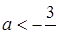 або
або  , то 1 розв’язок; якщо
, то 1 розв’язок; якщо  , то 2 розв’язки.
, то 2 розв’язки.
5. При яких значеннях  всі три корені рівняння
всі три корені рівняння  дійсні?
дійсні?
Розв’язання. Точка 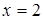 не є коренем рівняння при ні яких значеннях
не є коренем рівняння при ні яких значеннях  . Тому запишемо
. Тому запишемо  ,
,  .
.
Функція  спадає на кожному з проміжків
спадає на кожному з проміжків  та (
та (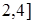 , а зростає на
, а зростає на 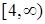 , причому
, причому  - точка мінімуму,
- точка мінімуму,  .
.
| x | (-¥, 2) | (2; 4) | 4 | (4; +¥) |
| a/ (x) | - | - | 0 | + |
| a (x) | ¯ | ¯ | 48 | |
Побудуємо графік функції  .
.

Рис.3.5
Ті значення  , для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. З рисунка видно, що
, для яких відповідні горизонтальні прямі перетинають побудований графік в трьох точках і будуть шуканими. З рисунка видно, що  .
.
Відповідь:  .
.
6. Розв’язати рівняння  . При яких значеннях параметра
. При яких значеннях параметра  добуток коренів менше найменшого кореня цього рівняння?
добуток коренів менше найменшого кореня цього рівняння?
Розв’язання. Із заданого рівняння одразу знаходимо  ,
,  ,
,  . Розглянемо функції
. Розглянемо функції  ,
,  ,
,  ,
,  . Побудуємо графіки цих функцій.
. Побудуємо графіки цих функцій.
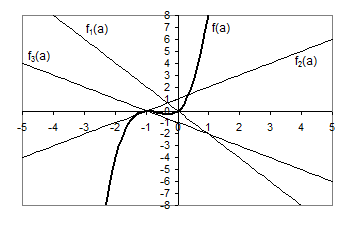
Рис.3.6
Необхідно знайти такі значення параметра, при яких графік  лежить нижче
лежить нижче
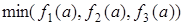 . Шукані значення
. Шукані значення  - це всі значення, менше
- це всі значення, менше  , де
, де  найменший корінь рівняння
найменший корінь рівняння  . Звідси знаходимо, що
. Звідси знаходимо, що 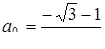 . Відповідь:
. Відповідь:  .
.
7. Визначити як розташовані корені рівняння 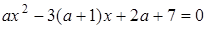 відносно відрізка
відносно відрізка  .
.
Розв’язання. Запишемо 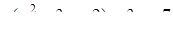 . Точки
. Точки 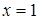 та
та 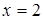 не є коренями заданого рівняння ні при яких
не є коренями заданого рівняння ні при яких  . Тоді
. Тоді  .
.
Знайдемо похідну

 або
або  .
.
Точка  - точка мінімуму,
- точка мінімуму,  - точка максимуму,
- точка максимуму, 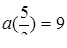 ,
,  .
.
Функція  спадає на кожному з проміжків
спадає на кожному з проміжків  та зростає на
та зростає на 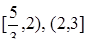 . Графік функції
. Графік функції  наведено на рис.3.7.
наведено на рис.3.7.

Рис.3.7
Розташування коренів рівняння відносно проміжку  можна визначити, перетинаючи побудований графік горизонтальними прямими. Далі через
можна визначити, перетинаючи побудований графік горизонтальними прямими. Далі через 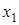 позначимо менший корінь, а через
позначимо менший корінь, а через  - більший.
- більший.
Якщо 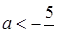 , то
, то  ; якщо
; якщо 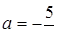 , то
, то 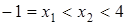 ;
;
якщо  , то
, то 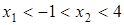 ; якщо
; якщо 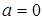 , то
, то 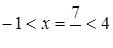 ;
;
якщо  , то
, то  ; якщо
; якщо 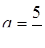 , то
, то  ;
;
якщо  , то
, то  ; якщо
; якщо 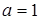 , то
, то  ;
;
якщо  , то рівняння коренів немає; якщо
, то рівняння коренів немає; якщо  , то
, то  ;
;
якщо  , то
, то  .
.
8. При яких значеннях параметра  рівняння
рівняння  має рівно два корені на відрізку
має рівно два корені на відрізку  ?
?
Розв’язання. Запишемо задане рівняння в такому вигляді:

Нехай  . Оскільки за умовою
. Оскільки за умовою 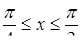 , то
, то  . Далі, знаходимо
. Далі, знаходимо
 ,
,  .
.
Побудуємо графік функції  для
для  . З
. З
находимо похідну  ,
,  ,
,  .
.
| x | (-1,  ) )
| 
| ( ; 0) ; 0)
|
| f/ (x) | - | 0 | + |
| f (x) | ¯ | 
| |
Побудуємо графік функції  для
для  .
.

Рис.3.8
Рівняння  має рівно два корені, якщо
має рівно два корені, якщо 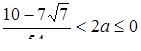 . Функція
. Функція  монотонна на
монотонна на  , а значить на цьому відрізку кожне своє значення приймає тільки один раз. Відповідь:
, а значить на цьому відрізку кожне своє значення приймає тільки один раз. Відповідь: 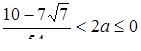 .
.
9. При яких дійсних  рівняння
рівняння  має більше одного кореня на відрізку
має більше одного кореня на відрізку  ?
?
Розв’язання.
Перепишемо рівняння у вигляді


Нехай 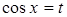 , оскільки за умовою
, оскільки за умовою  , то
, то  .
.
Далі знаходимо,  .
.
Похідна дорівнює
 ,
,
 ,
,  ,
,
 ,
, 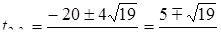
Побудуємо графік функції  (рис.3.9).
(рис.3.9).
Знайдемо a
( ) =
) =  , a (
, a ( ) =
) =  .
.

Рис.3.9
Рівняння  має більше одного кореня, якщо
має більше одного кореня, якщо  .
.
Приблизно це  .
.
Відповідь:  .
.
10. При яких  рівняння
рівняння  має рівно чотири корені?
має рівно чотири корені?
Розв’язання. Побудуємо графіки функцій
 та
та
 .
.

Рис.3.10
Рівняння має чотири розв’язки, коли графік  перетинає
перетинає 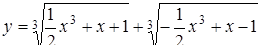 в чотирьох точках (див. рис.3.10)
в чотирьох точках (див. рис.3.10)
Відповідь:  .
.
Задачі для самостійної роботи
1. Знайти всі значення  , при яких рівняння
, при яких рівняння  має єдиний розв’язок.
має єдиний розв’язок.
Відповідь:  або
або  .
.
2. Знайти всі значення  , при яких для всіх
, при яких для всіх 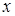 за модулем не перевищуючих 1, виконується нерівність:
за модулем не перевищуючих 1, виконується нерівність:

Відповідь:  або
або  .
.
3. Знайти всі  , при кожному з яких область визначення функції
, при кожному з яких область визначення функції  не перетинається з множиною
не перетинається з множиною  .
.
Відповідь:  .
.
4. При яких  знайдеться
знайдеться  з інтервала (0,1) таке, що рівняння
з інтервала (0,1) таке, що рівняння  має хоча б два розв’язки на інтервалі
має хоча б два розв’язки на інтервалі  ?
?
Відповідь:  .
.
5. При  - більший з коренів рівняння
- більший з коренів рівняння  . Знайти найбільше значення
. Знайти найбільше значення 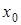 при
при  ,
,  .
.
Відповідь: 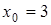 .
.
 2020-01-14
2020-01-14 112
112








