Вопрос о термодинамической возможности осуществления и направления реакций в заданных условиях решается на основе уравнения изотермы химической реакции
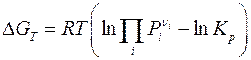
где 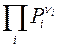 – произведение неравновесных (фактических) давлений реагентов в степенях
– произведение неравновесных (фактических) давлений реагентов в степенях 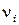 , соответствующих стехиометрическим коэффициентам в уравнении реакции.
, соответствующих стехиометрическим коэффициентам в уравнении реакции.
Для реакций
2Н2 + О2 = 2Н2О; (1)
2СО + О2 = 2СО2; (2)
Константы равновесия реакций (1) и (2)
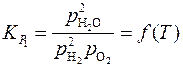
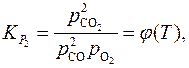
а уравнения изотерм химических реакций (1) и (2) имеют вид:
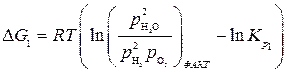 ,
,
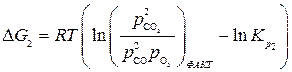 .
.
Если условия, характеризующие состояния системы (фактическое в реакторе и равновесное по расчету) таковы:
 и
и 
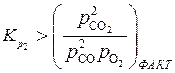 ,
,
то выполняется термодинамическое условие протекания процесса (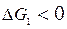 и
и 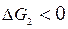 ), и в этих условиях реакции горения (1) и (2) должны идти в прямом направлении.
), и в этих условиях реакции горения (1) и (2) должны идти в прямом направлении.
Термодинамический анализ реакции водяного газа.
Н2+СО2=СО+ Н2О 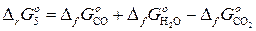 (5)
(5)
Подставляя необходимые для вычислений значения 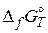 получаем:
получаем:
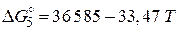 (Дж).
(Дж).
Правило фаз Гиббса
f = k + 2 – n,
где f – число степеней свободы системы, вариантность системы;
k – число независимых компонентов;
n – число фаз.
Число независимых компонентов k = q–r,
где q – общее число веществ в системе; r – число независимых реакций между ними.
k = 3; n = 1 → f = 4
Реакция (5), называемая реакцией водяного газа, определяет соотношение между углеродсодержащими газами СО – СО2 и водородсодержащими Н2 – Н2О в равновесных сложных газовых смесях. При этом из выражения константы равновесия  следует пропорциональность
следует пропорциональность 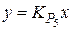 (при введении обозначений
(при введении обозначений 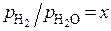 и
и  ). Функцию
). Функцию 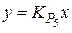 можно представить графически (рис. 1.6). Для расчета
можно представить графически (рис. 1.6). Для расчета 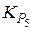 применяют уравнение
применяют уравнение 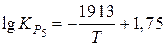 , полученное из выражения
, полученное из выражения 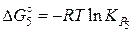 при подстановке в него зависимости
при подстановке в него зависимости 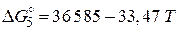
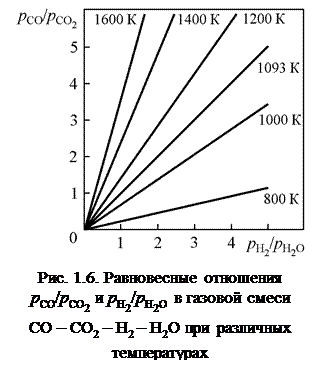 Следует отметить, что представленные простейшие изотермические зависимости дают строгую связь отношений
Следует отметить, что представленные простейшие изотермические зависимости дают строгую связь отношений 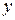 и
и 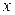 , но указывают и на неопределенность равновесных составов газовых смесей. Из графика при заданной температуре и значении
, но указывают и на неопределенность равновесных составов газовых смесей. Из графика при заданной температуре и значении 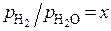 можно определить равновесное с x отношение
можно определить равновесное с x отношение  и наоборот. Зная состав газовой атмосферы металлургического агрегата или системы, можно на основе графика решить вопрос о равновесности газовой фазы и спрогнозировать протекание процессов изменения ее состава и свойств. Если одно из отношений при определенной температуре на графике не соответствует другому, то смесь неравновесна. Ее следует рассматривать как исходную, и выполнить расчет равновесного состава сложного газа.
и наоборот. Зная состав газовой атмосферы металлургического агрегата или системы, можно на основе графика решить вопрос о равновесности газовой фазы и спрогнозировать протекание процессов изменения ее состава и свойств. Если одно из отношений при определенной температуре на графике не соответствует другому, то смесь неравновесна. Ее следует рассматривать как исходную, и выполнить расчет равновесного состава сложного газа.
Все точки на изотермической прямой соответствуют состояниям системы с одним и тем же значением 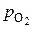 . Это означает, что различные по составу двухкомпонентные смеси характеризуются одинаковым сродством к кислороду и одинаковыми окислительно-восстановительными свойствами. При 1093 К, как было отмечено в примере 1.1, сродство к кислороду у водорода и СО одинаково, и это проявляется на графике равенством отношений (
. Это означает, что различные по составу двухкомпонентные смеси характеризуются одинаковым сродством к кислороду и одинаковыми окислительно-восстановительными свойствами. При 1093 К, как было отмечено в примере 1.1, сродство к кислороду у водорода и СО одинаково, и это проявляется на графике равенством отношений (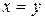 ), так как
), так как  при 1093 К. При всех других температурах равноценные по окислительно-восстановительным свойствам смеси имеют разные составы. Например, из графика следует, что смеси Н2 – Н2О с отношением
при 1093 К. При всех других температурах равноценные по окислительно-восстановительным свойствам смеси имеют разные составы. Например, из графика следует, что смеси Н2 – Н2О с отношением 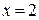 при 1400 К соответствует смесь СО – СО2 с отношением
при 1400 К соответствует смесь СО – СО2 с отношением 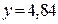 .
.
Состав равновесной газовой фазы, образующейся из смеси СО2 и Н2 можно определить либо строгим расчетом, либо упрощенным.
В первом случае нужно записать систему уравнений связи между переменными, задавшись в качестве независимых параметров температурой, давлением и исходным составом газовой фазы. Выбираем Р, Т, j = [H]/[O], y = [H]/[С]
Тогда 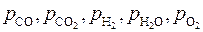 – неизвестные (вычисляемые) переменные.
– неизвестные (вычисляемые) переменные.
Система уравнений связи:
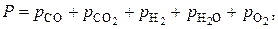
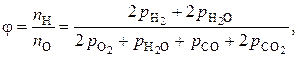
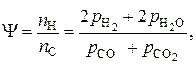
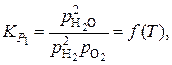
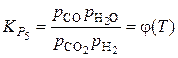
Упрощенный расчет основан на том, что при температурах пирометаллургических процессов значение 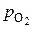 весьма мало. Тогда вначале рассчитываем состав равновесной фазы без учета присутствия в ней кислорода, то есть в расчете учитываем только равновесие по реакции (5).
весьма мало. Тогда вначале рассчитываем состав равновесной фазы без учета присутствия в ней кислорода, то есть в расчете учитываем только равновесие по реакции (5).
Для этого записываем уравнение реакции водяного газа (5) и вводим обозначения, характеризующие исходное и равновесное состояния газовой фазы:
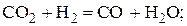
исходный состав, моль a b – –
равновесный состав, моль a – x b– x x x
 . (
. (
Отсюда получаем квадратное уравнение и находим х.
Равновесное давление кислорода находим из выражений для константы равновесия реакции (1):
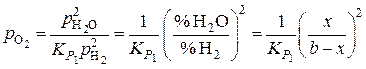
или реакции (2):
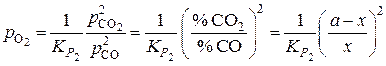
 2020-01-14
2020-01-14 181
181








