Значення параметрів ресивера в номінальноу статичному режимі

№ п.п	Назва параметру	Позначення	Розмірність	Числові значення
1.	Тиск повітря на вході		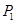Н/см2	80
2.	Тиск повітря в першій ємкості		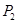Н/см2	50
3.	Тиск повітря в другій ємкості		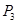Н/см2	16
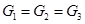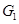
4.	Витрати повітря ()		Кг/год	60
5.	Об'єм першої ємкості		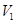м3	3
6.	Об'єм другої ємкості		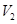м3	5
7.	Ступінь відкриття клапану		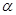-	0.5
8.	Щільність повітря на вході		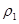Кг/м3	11.9
9.	Щільність повітря в перщій ємкості		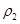Кг/м3	7.9
10.	Щільність повітря в другій ємкості.		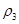Кг/м3	3.42
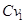
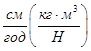
11.	Коефіцієнт витрати через клапан			6.35
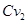
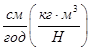
12.	Коефіцієнт витрати парубка між ємкостями			3.6
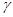
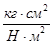
13.				0.133

 

Користуючись розрахованими значеннями В, D, C та Е, а також значеннями параметрів із таблиці 1, з використанням залежностей обчислимо значення коефіціентів рівняння динаміки.

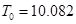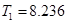 год²; год; ; ; .

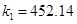
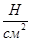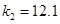
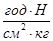Підставляючи значення коефіцієнтів у рівняння динаміки запишемо його у числовій формі

 

.

 

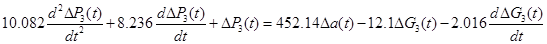Це рівняння є рівнянням динамікт ресивера відповідно до залежності .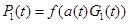

Знайдемо розв'язання рівняння

 

 

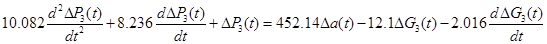
у вигляді 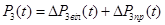, де 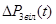 - вільна складова;  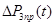- примусова складова.

Початкові умови приймемо нульовими: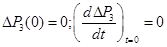

Керуючий вплив визначаємо наступним чином: 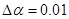. Збурюючий вплив  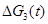та його похідну приймаємо нульовими. Харакеристичне рівняння диференційного рівняння має вид: , ; .

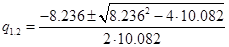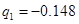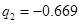Таким чином вільна складова вирішення має наступний вид:

 

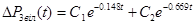
де, С₁ та С₂ – сталі інтегрування.

Примусова складова, у урахуванням того, що 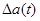 не залежить від часу, складе:

 

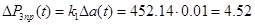Н/см²

 

Для визначення сталих інтегрування С₁ та С₂ складемо систему равняння з урахуванням початкових умов та того, що похідна від 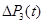 має наступний вид:

 

 

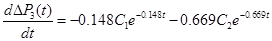
Система рівнянь формується наступним чином:

 

 

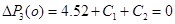
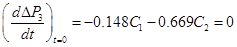
Звідси маємо:

 

 

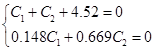
Розв'язання системи рівняння дозволяє отримати такі значення С₁ та С₂:

, .

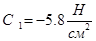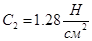Таким чином, остаточно запишемо розв'язання рівняння

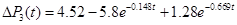
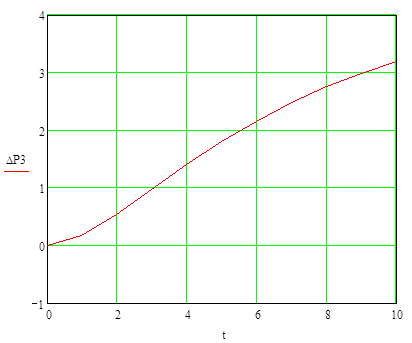
За цією формулою проведемо розрахунки , результати яких наведені в таблиці.

 

 

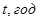
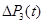
0	0
1	0,174
2	0,542
3	0,972
4	1,399
5	1,798
6	2,157
7	2,474
8	2,751
9	2,992
10	3,201